Использование суррогатных моделей электрофизических характеристик для проектирования высоковольтных изоляторов с учетом потенциального наличия дефектов

A.V. Korzhov, ,

P.V. Lonzinger, ,

V.I. Safonov, ,

V.A. Surin, ,

Ya.V. Bushmelev, ,

K.N. Belov, ,

Изменения характеристик изоляционных конструкций могут быть востребованы в случае адаптации конструкций для работы в новых условиях. Например, такая оценка актуальна при рассмотрении возможности работы изоляторов, спроектированных для частоты 50 Гц, в линиях постоянного тока [1]. Проектирование изоляционных конструкций с измененными характеристиками связано с выбором подходящей геометрии [2, 3], изолирующих материалов [4, 5], а также с учетом старения изоляции и воздействия внешних факторов [6]. В изоляционных конструкциях возможно возникновение дефектов на этапе производства. В зависимости от геометрической формы конструкции, возникающих дефектов, а также свойств материалов дефекты могут проявлять себя в различной степени во время эксплуатации [7, 8]. Для широко применяемых изоляционных конструкций существуют стандарты на наличие допустимых дефектов (например, на основе стеклянных подвесных изоляторов ‒ стандарт [9]). При изменении геометрии или свойств материалов изоляционной конструкции может потребоваться уточнение требований к допустимости присутствующих дефектов. Это связано с изменением в рассматриваемых случаях картин распределения электрического поля внутри конструкций, а значит, и параметров дефектов, при которых ожидается нарушение электрической прочности (опасных дефектов).

Для сопоставления различных вариантов изоляционных конструкций с точки зрения допустимости дефектов требуется применение эффективного инструмента, на основе которого можно проводить оценку распределения электрического поля в области расположения дефекта. В качестве тако- го инструмента могут выступать полиноминальные суррогатные модели, рассмотренные в [10]. В упомянутой публикации приведены общие подходы к построению суррогатных моделей при оценке характеристик поля в области расположения дефекта внутри изоляционной конструкции с границами со сложной геометрической формой. Также в публикации рассмотрено построение частной суррогатной модели для изучения влияния формы и расположения дефекта внутри головки стеклянной детали изолятора ПС-70Е на характеристики электрического поля в области дефекта. Для оценки влияния геометрии изоляционной конструкции и свойств материалов необходимо построение соответствующих частных суррогатных моделей, чему и посвящена настоящая работа.

Подходы и методы исследования

Для исследования выбрана головка стеклянного изолятора ПС-70Е. Как и в [10], исследование ограничивается внутренними дефектами, не имеющими непосредственного контакта с поверхностью. Дефекты имеют форму эллипсоидов с осями a, b и с, физические свойства материалов изолятора и дефекта определяются диэлектрической проницаемостью Ео и удельной проводимостью уо для изолятора и аналогичными величинами Ед и уд для дефекта. Распределение электрического поля внутри дефекта описывается максимальной, минимальной и средней напряженностью электрического поля (Emax, Emin и Eav). Для проведения исследования выбираются полиноминальные суррогатные модели. Данные, на основе которых строятся суррогатные модели, получены с помощью конечно-элементного моделирования. При этом набор значений независимых аргументов выбира- ется на основе метода латинского гиперкуба. Имитационная модель ограничена областью объекта, прилегающей к дефекту. Внутренняя (под высоким потенциалом, большей кривизны) и внешняя (под низким потенциалом, меньшей кривизны) границы области имеют сложную форму, образованную вращением вокруг оси соответствующих кривых. Образующие границ описываются в виде периодических функции одной переменной и задаются рядами Фурье. Справедливо допущение об отсутствии зависимости потенциалов точек границ от пространственных координат. Расчет проводится при квазистационарной формулировке задачи в частотной области. Потенциал внешней границы считаем равным нулю, потенциал внутренней границы – синусоидальной функцией амплитудой 1 В и частотой 50 Гц. Как и в [10], можно говорить об относительной напряженности электрического поля, измеряемой в 1/м.

Исследование влияния свойств материалов

Для построения суррогатной модели при изменении свойств материалов применялась имитационная модель, геометрия которой показана на рис. 1. Форма дефекта описывается в виде эллипсоида с полуосями, расположенными параллельно координатным осям X, Y и Z. Положение дефекта определяется параметрами d иг. Переменная d характеризует расположение центра включения над плоскостью Z = 0, параметр г - удаленность центра дефекта от оси вращения. Положение дефекта и его геометрические размеры взяты для случая, при котором наблюдается максимальная напряженность электрического поля среди рассмотренных в [10] случаев: d = 10 мм; г = 2 мм; a = 1 мм; b = 0,1 мм; с = 1 мм. Диапазоны изме-

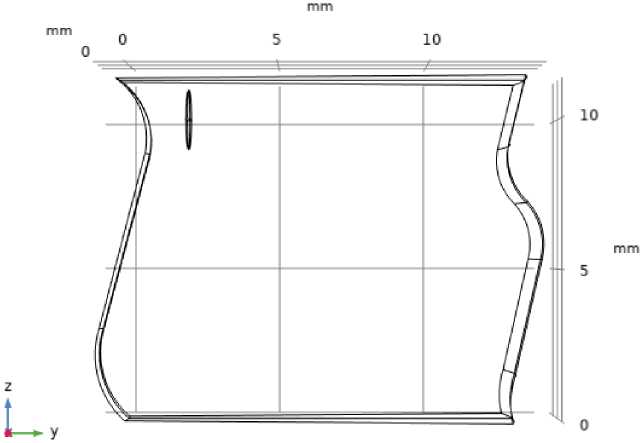
Рис. 1. Геометрия имитационной модели для суррогатной модели, учитывающей изменение свойств материалов

Fig. 1. Geometry of the simulation model for a surrogate model that takes into account changes in material properties

нения переменных параметров: Е_о и Е д - от 1 до 10; у₀ - от 10 “⁸ до 10 • 10 “⁸ См/м; у д - от 10 ^-10 до 10 • 10 -¹⁰ См/м.

Суррогатная модель была реализована в виде полинома для 4 переменных вида

^(Е о ,Е д ,У 0 ,У д ) =

У ^л ^ ( = 0

S (s+t+u+v=i) Р хГиу^Ео

чччг.

Здесь и - степень полинома; e_stur - коэффициенты, вычисляемые методом наименьших квадратов. Во внутренней сумме участвуют слагаемые со всеми возможными комбинациями показателей степеней, подчиняющихся условию s + t + u + v = i. Оптимальная степень полинома была получена в результате итерационного процесса, связанного с увеличением числа точек в гиперкубе и с повышением степени полиномов. При размере гиперкуба в 20 000 точек и 7-й степени полинома максимальные погрешности для E_max и E_min составили 11,2 и 10,7 % соответственно.

На рис. 2 показаны зависимости для относительных максимальных Emax *, средних Eav * и минимальных Emin * напряженностей поля. Анализ зависимостей на рис. 2 позволяет говорить о том, что определяющими факторами являются удельная проводимость вещества объекта у0 и диэлектрическая проницаемость вещества дефекта Ед. Диэлектрическая проницаемость Ео оказывает существенное влияние на напряженность поля только при Ед < 6, что характерно для дефектов в виде газовых включений.

Исследование влияния изменений геометрии объекта

В качестве дефекта рассмотрим воздушное включение диаметром 2 мм. Базовая форма внешней и внутренней границ детали взята из предыдущей модели. Для модификации внешней и внутренней границ вводятся параметры к1_1 и к2_1 соответственно. Амплитуды первых гармоник образующих границ находятся умножением исходных амплитуд (как в модели на рис. 1) на указанные множители. Изменение положения воздушного включения описывается так же, как и ра-

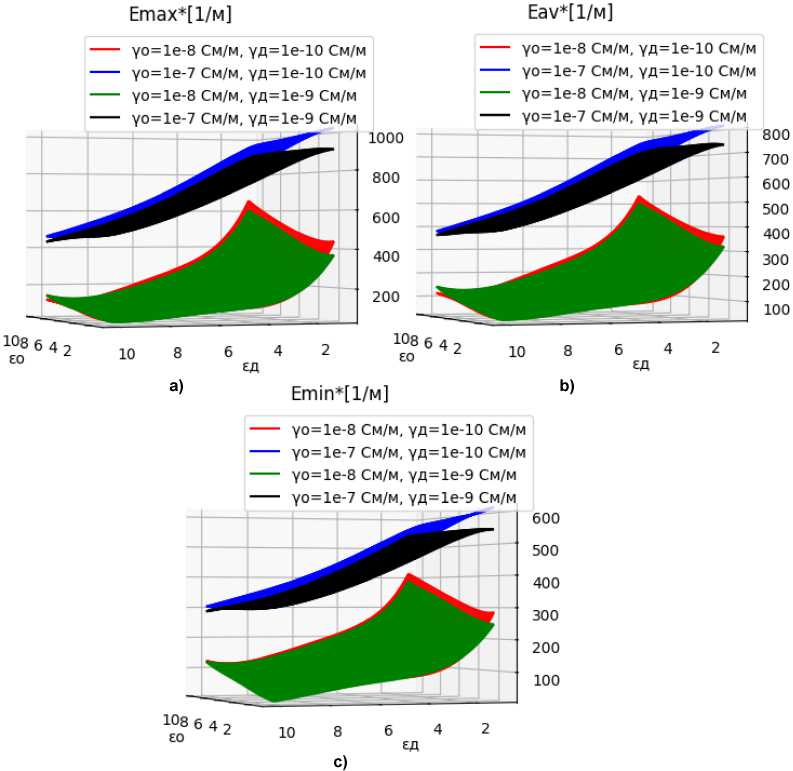
Рис. 2. Зависимости максимальной напряженности поля дефекта при изменении диэлектрических проницаемостей и удельных проводимостей объекта и дефекта Fig. 2. Dependences of the maximum field strength of the defect when changing the dielectric permittivity and specific conductivities of the object and the defect

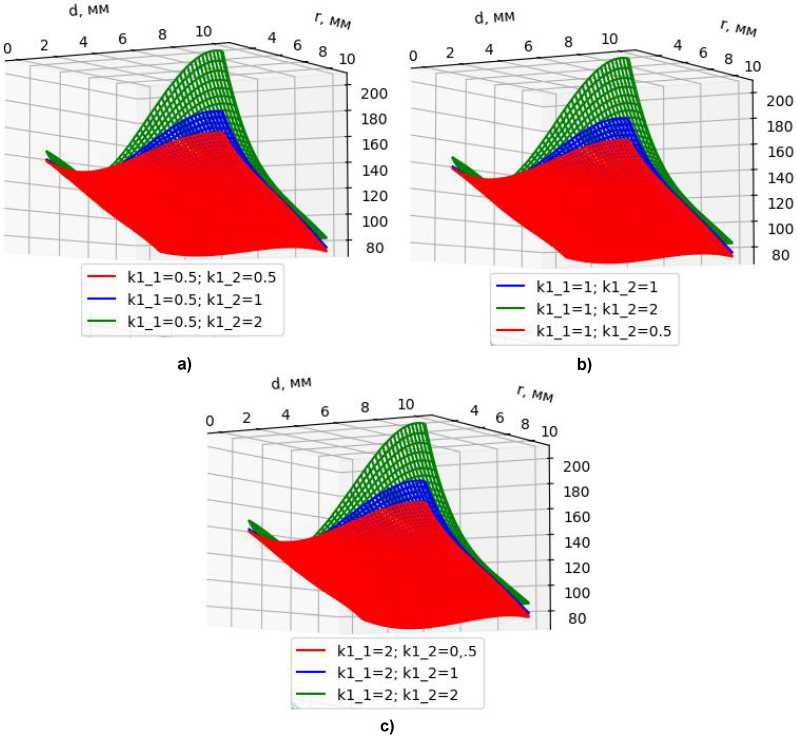
Рис. 3. Зависимости максимальных напряженностей поля дефекта при изменении формы границ объекта и местоположения дефекта Fig. 3. Dependences of the maximum strengths of the defect field when changing the shape of the object's edges and the location of the defect

нее, параметрами г и d. При моделировании принят следующий диапазон изменения параметров: к1_1 и к2_1 - от 0,5 до 2; г - от 3 до 11 мм; d - от 1 до 10 мм. Остальные параметры взяты из модели в [10].

Для составления суррогатной модели используется выражение, подобное (1), при соответствующей замене независимых переменных на перечисленные выше параметры. В рассматриваемом случае для 4 переменных оптимальными является полином 5-й степени при размере гиперкуба в 20 000 точек. Максимальная погрешность при этом не превышает 7,6 % (для минимальных напряженностей поля).

Зависимости, соответствующие полученным суррогатным моделям для максимальной напряженности поля в дефекте, показаны на рис. 3. Ожидаемым является наличие повышенных величин напряженностей поля в области наименьших значений параметра г (при приближении дефектов к границе с наибольшим потенциалом). Анализ полученных зависимостей показывает, что форма внутренней границы оказывает существенное влия- ние на величины напряженности поля только для дефектов, расположенных вблизи нее (г < 5 мм). При этом имеется прямая связь между амплитудой первой гармоники образующей внутренней поверхности и напряженностями поля. Изменение формы внешней границы (амплитуды первой гармоники) приводит к изменениям напряженностей поля не более чем на 10 %, что лежит в рамках погрешности разработанных суррогатных моделей.

Обсуждение результатов

В соответствии с подходом, примененным в [11], электрическая прочность вещества дефекта может быть оценена по следующим условиям: ^ (max(^), min ^) =

( «НЭП», если max(F) и min(E) >  Е кр ;

«ВНЭП», если max(E) > Екр и min(E) < Екр; (2) «ЭПНН», если max(E) и min(E) < Екр.

Здесь max(E) и min(E) - соответственно макси- мальная и минимальная напряженности электрического поля внутри дефекта. В дефектах из категории «НЭП» будет наблюдаться развитие пер- вичного разряда, из категории «ЭПНН» – электрическая прочность не будет нарушена. Для промежуточной категории «ВНЭП» требуются дополни- тельные исследования для определения возможно- сти развития первичного разряда.

Рассмотрим особенности применения условия (2) для рассмотренных суррогатных моделей. Нарушение электрической прочности твердого диэлектрического объекта в области расположения эллиптического дефекта без полного перекрытия изоляционного промежутка (частичный разряд)

имеет смысл только при наличии газовых включений. При газообразном включении в соответствии с [12] критическая напряженность определяется по формуле

^ кр =H3J1+^).

Здесь р - давление, Па; ( | ) , В и п - коэффициенты, зависящие от типа газообразного вещества; а - размер полуоси эллипсоида, направленной вдоль градиента поля. Для воздушных включений: ( - ) = 25,2 В • Па^-1 • м " ¹; В = 8,6 м ! • Па ! и п = 0,5;

PJcr давление р = 105 Па.

Для стеклянных деталей изолятора ПС-70Е, согласно [11], необходимо рассматривать напряжение U = 57 670 В. При известных геометриче- ских размерах головки изолятора получаем, что первое из условий (2) справедливо для всей рассмотренной области изменения параметров d и г и диэлектрической проницаемости вещества дефекта Ед < 4, что соблюдается для газовых включений. Исключением является небольшая область около внешней границы (с потенциалом земли), соответствующая условию г > 10,55 мм. Изменение формы границы объекта при этом незначительно меняет размеры указанной области (не более чем на 2 %). Для минимальных напряженностей поля соотношения (2) соблюдаются при г < 9,5 мм, диэлектрической проницаемости вещества дефекта Ед <3 и удельной проводимости вещества объекта у0 > 2,7 • 10-7 См/м. Таким образом, согласно проведенному анализу и в соответствии с полученными ранее в [10] зависимостями, можно сделать вывод, что потенциально опасными с точки зрения нарушения электрической прочности являются дефекты размерами от 0,1 до 2 мм. Указанный диапазон должен быть уточнен в дальнейшем при разработке суррогатных моделей, справедливых в общем случае.

Недостатком рассмотренных моделей является достаточно узкий диапазон изменения параметров границ и свойств вещества. Построение полных суррогатных моделей, в которых возможны изменения границ за счет вариации амплитуд и фаз высших пространственных гармоник, приве- дет к увеличению числа свободных параметров. В этом случае применение полиноминальных моделей приведет к значительному усложнению моделей, приводящему к существенным затратам вычислительных ресурсов.

В качестве дальнейшего развития рассмотренных подходов можно рассматривать построение суррогатных моделей, в которых свободными параметрами выступают напряженности электрического поля в некой окрестности дефекта. Окрестность должна быть выбрана таким образом, чтобы относительная разность между напряженностью поля при наличии дефекта в изоляционной детали и напряженностью в той же точке при отсутствии дефектов не превышала заранее выбранного допустимого значения (например, 10 %). Тогда конкретные значения напряженностей поля как независимых аргументов могут быть найдены, исходя из результатов однократного конечноэлементного моделирования. При таком подходе ожидается значительное снижение числа свободных параметров за счет отсутствия необходимости точного описания границ изоляционной детали. Вопросы построения суррогатных моделей при таком подходе требуют дальнейших исследований.

Заключение

На примере геометрии стеклянной детали изолятора ПС-70Е с эллиптическими внутренними дефектами показано получение суррогатных моделей в случаях: а) при изменении свойств материалов объекта и дефекта и фиксации остальных параметров; б) при изменении формы границ объекта, расположения дефекта и фиксации других параметров. Все суррогатные модели были полиномиальными, максимальной степенью полинома при учете свойств материалов, равной 7, при учете геометрии границ ‒ 5. Максимальная погрешность модели с учетом свойств материалов составила 11,2 %, с учетом геометрии границ ‒ 7,6 %. С использованием полученных зависимостей и результатов в [10] установлены соотношения для размеров потенциально опасных дефектов: от 0,1 до 2 мм.

Полученные суррогатные модели можно использовать в системе автоматизированного проектирования и как элементы мультифизических моделей при совпадении набора параметров и диапазона их изменения. Для других условий необходимо использовать общие рекомендации, которые были выработаны при составлении примеров суррогатных моделей. Дальнейшим развитием полученных результатов является разработка универсальных суррогатных моделей, позволяющих получать зависимости характеристик распределения электрического поля без подробного учета геометрической формы границ изоляционной детали.