Использование суррогатных моделей при построении множества парето позиционного электропневматического привода с дискретными пневмораспределителями
Автор: Шейкин М.О., Черкасских С.Н., Шилин Д.В., Феденков В.В.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 1 т.25, 2025 года.
Бесплатный доступ
Введение. Пневматические приводы находят широкое применение в промышленности благодаря своей надежности, простоте конструкции и способности функционировать в сложных условиях. Однако при решении задач позиционирования использование традиционных пропорциональных распределителей зачастую оказывается избыточным, что ведет к неоправданному увеличению стоимости и усложнению конструкции. Применение более простых дискретных распределителей сталкивается с проблемой, связанной с необходимостью достижения компромисса между частотой их переключения и точностью позиционирования. Существующие исследования, в основном, фокусируются на оптимизации отдельных показателей качества работы пневмоприводов и не предлагают эффективных методов поиска компромисса между конфликтующими критериями. Использование классических методов построения множества Парето для многокритериальной оптимизации требует значительных вычислительных ресурсов, что затрудняет их практическое применение. Целью исследования является разработка методологии многокритериальной оптимизации параметров позиционного электропневматического привода с дискретными распределителями на основе построения множества Парето с использованием суррогатных моделей, позволяющей найти оптимальный баланс между частотой переключений и точностью позиционирования.
Пневмопривод, дискретные распределители, скользящее управление, многокритериальная оптимизация, суррогатные модели
Короткий адрес: https://sciup.org/142244389
IDR: 142244389 | УДК: 62.621 | DOI: 10.23947/2687-1653-2025-25-1-52-64
Текст научной статьи Использование суррогатных моделей при построении множества парето позиционного электропневматического привода с дискретными пневмораспределителями
Оригинальное эмпирическое исследование
Введение . Пневматические приводы находят широкое применение в промышленности благодаря своей надежности, простоте конструкции и способности функционировать в сложных условиях. Однако при решении задач позиционирования использование традиционных пропорциональных распределителей зачастую оказывается избыточным, что ведет к неоправданному увеличению стоимости и усложнению конструкции. Применение более простых дискретных распределителей сталкивается с проблемой, связанной с необходимостью достижения компромисса между частотой их переключения и точностью позиционирования.
Существующие исследования, в основном, фокусируются на оптимизации отдельных показателей качества работы пневмоприводов и не предлагают эффективных методов поиска компромисса между конфликтующими критериями. Использование классических методов построения множества Парето для многокритериальной оптимизации требует значительных вычислительных ресурсов, что затрудняет их практическое применение.
Целью исследования является разработка методологии многокритериальной оптимизации параметров позиционного электропневматического привода с дискретными распределителями на основе построения множества Парето с использованием суррогатных моделей, позволяющей найти оптимальный баланс между частотой переключений и точностью позиционирования.
Материалы и методы. Исследование проводилось на модели позиционного пневмопривода с дискретными распределителями, реализованной в MATLAB Simulink. Для анализа параметров использовался метод латинского гиперкуба, который обеспечивает равномерное заполнение пространства параметров. Для снижения вычислительных затрат были применены суррогатные модели, построенные с использованием нейронных сетей. В качестве алгоритма управления было выбрано скользящее управление, которое эффективно компенсирует внешние возмущения и неопределенности системы.
Результаты исследования . Оптимизация параметров управления показала возможность достижения высокой точности позиционирования при минимальной частоте переключений распределителей. Использование метода латинского гиперкуба обеспечило равномерное распределение расчетных точек, что позволило построить точную суррогатную модель. Экспериментально было доказано, что предложенный подход снижает вычислительные затраты на 48 %, сохраняя высокую точность моделирования и анализа.
Обсуждение и заключение . Результаты исследования подтверждают, что скользящее управление является эффективным решением для дискретных пневмоприводов в контексте многокритериальной оптимизации. Разработанный подход позволяет значительно уменьшить частоту переключений распределителей без ощутимых потерь в качестве переходных процессов, что способствует продлению сроков службы оборудования и повышению надежности автоматизированных систем. Использование суррогатных моделей и нейросетевых технологий открывает новые перспективы для более быстрого проектирования сложных систем.
Original Empirical Research
Using Surrogate Models in the Construction of a Pareto-Optimal Positioning Electropneumatic Actuator with Discrete Pneumatic Valves
Maxim O. SheykinM, Sergey N. Cherkasskikh , Denis V. Shilin , Vladimir V. Fedenkov
Introduction . Pneumatic actuators are widely used in industry due to their reliability, simplicity of design, and ability to operate under complex conditions. However, when solving positioning problems, the use of traditional proportional valves is often redundant, which causes an unjustified increase in cost and complexity of the design. The application of simpler discrete distributors faces the problem related to the need to reach a compromise between their switching frequency and positioning accuracy.
Existing studies mainly focus on optimizing individual performance indicators of pneumatic actuators and do not offer effective methods for finding a compromise between conflicting criteria. Using classical methods for constructing a Pareto set for multicriteria optimization requires significant computational resources, which complicates their practical application.
The research objective is to develop a methodology for multicriteria optimization of the parameters of a positioning electropneumatic actuator with discrete distributors based on the construction of a Pareto set using surrogate models, which provides finding the optimal balance between switching frequency and positioning accuracy.
Materials and Methods . The research was conducted on a model of a positioning pneumatic actuator with discrete distributors, implemented in MATLAB Simulink. The Latin hypercube method was used to analyze the parameters, which provided uniform filling of the parameter space. To reduce computational costs, surrogate models, built using neural networks, were used. Sliding control was selected as a control algorithm, which effectively compensated for external disturbances and uncertainties of the system.
Results . The optimization of control parameters has shown the possibility of reaching high positioning accuracy with a minimum frequency of distributor switching. The use of the Latin hypercube method provided a uniform distribution of the calculation points, which made it possible to construct an accurate surrogate model. It has been experimentally proven that the proposed approach reduces computational costs by 48%, while maintaining high accuracy of modeling and analysis.
Discussion and Conclusion . The research results confirm that sliding control is an effective solution for discrete pneumatic drives in the context of multicriteria optimization. The developed approach makes it possible to significantly reduce the frequency of switching distributors without substantial losses in the quality of transients, which helps to extend the service life of equipment and increase the reliability of automated systems. The use of surrogate models and neural network technology opens up new prospects for faster design of complex systems.
Машиностроение и машиноведение
Введение. Пневматические приводы находят широкое применение в различных областях промышленности благодаря простоте их конструкции, возможности обеспечения высоких скоростей движения объектов управления, экологичности, пожаробезопасности, возможности работы в агрессивных средах.
В системах, ориентированных на слежение, для управления пневмоприводом обычно используются пропорциональные распределители, которые обеспечивают непрерывное регулирование. Однако, когда основной задачей пневмопривода является позиционирование выходного звена в заданном положении, а не следование заданной траектории, применение таких распределителей может оказаться излишним. В данной ситуации целесообразно рассмотреть использование более простых дискретных распределителей [1] .
Существующие исследования предлагают разнообразные подходы к управлению позиционированием, включая алгоритмы с использованием широтно-импульсной модуляции, а также принципы скользящего и прогнозного управления [2]. Повышение точности позиционирования достигается либо модификацией алгоритма управления вблизи точки останова [3], либо посредством внедрения специализированных механических или гидравлических тормозных устройств [4]. Тем не менее, несмотря на улучшение точности, использование тормозных устройств значительно усложняет конструкцию, что в свою очередь может свести на нет преимущества применения дискретных пневмораспределителей [5].
Анализ современного состояния исследований выявил существенные пробелы в текущем понимании проблемы. В первую очередь, отсутствует целостный подход к оценке эффективности различных структур позиционных электропневматических приводов с дискретными клапанами. Кроме того, недостаточно проработан вопрос достижения компромисса между частотой переключений распределителей и качеством позиционирования. Существующие методики многокритериальной оптимизации параметров таких систем не обеспечивают необходимой эффективности. Авторы публикаций часто сосредотачиваются на отдельных аспектах качества, таких как точность или быстродействие. Слабое внимание уделяется взаимосвязи между повышением точности позиционирования и увеличением частоты переключений распределителей, что напрямую сказывается на износе оборудования и его сроке службы.
В пенвмоприводе, рассматриваемом в данной работе, не предусмотрены специальные тормозные устройства, и позиционирование выходного звена в заданной точке осуществляется исключительно за счет переключения дискретных пневмораспределителей в нужные моменты времени, согласно применяемым алгоритмам управления. Это обеспечивает простоту конструкции и низкую стоимость решения, однако приводит к частому переключению пневмораспределителей. Строгость требований к качеству переходного процесса, в свою очередь, неизбежно ведет к росту числа переключений.
Таким образом, возникает необходимость в поиске компромиссного решения, принимающего во внимание два противоречивых критерия: точность позиционирования и интенсивность работы распределителей. Построение фронта Парето позволит определить множество неулучшаемых решений, где невозможно повысить один показатель качества без ухудшения другого, что предоставит разработчику возможность оправданного выбора параметров системы. Однако традиционные методы построения множества Парето требуют многократных расчетов сложных динамических моделей [6] , что делает процесс крайне трудоемким и затратным по времени.
Применение суррогатных моделей при построении множества Парето [7] открывает новые горизонты для решения данной проблемы, хотя и требует разработки специализированных методик, адаптированных для конкретного класса пневматических устройств.
Целью данной работы является разработка методики многокритериальной оптимизации параметров позиционного электропневматического привода с дискретными клапанами, основанной на использовании суррогатных моделей, которая обеспечит эффективный поиск компромиссных решений между частотой переключений и качеством позиционирования. Для достижения этой цели необходимо разработать методику создания суррогатной модели для оценки показателей качества позиционного электропневматического привода. Также потребуется создать алгоритм многокритериальной оптимизации параметров привода с использованием суррогатной модели и провести исследование эффективности предложенного подхода на конкретной конструкции привода.
Материалы и методы. В рамках данной работы рассматривается позиционный пневмопривод с дискретными пневмораспределителями без специальных тормозных устройств, изображенный на рис. 1. Он содержит одноштоковый пневмоцилиндр двухстороннего действия, управляемый четырьмя пневмораспределителями 2/2. Использование четырех пневмораспределителей 2/2 вместо двух пневмо-распределителей 3/2 позволяет обеспечить лучшие динамические характеристики пневмопривода при допустимом удорожании конструкции.
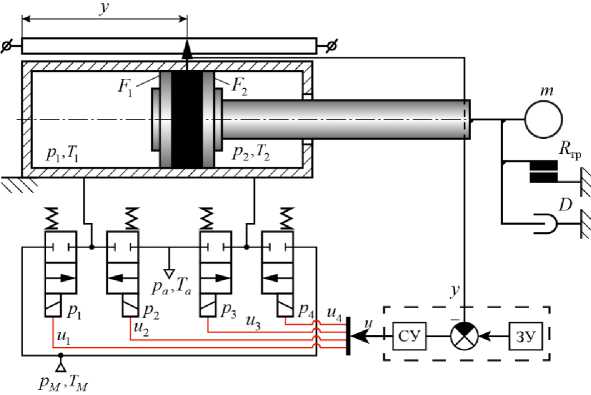
Рис. 1. Схема пневмопривода с дискретными распределителями
Для управления дискретными пневмораспределителями используется система управления (СУ), представленная на рис. 2. Она реализует принцип скользящего управления в соответствии с входным сигналом, определяемым задающим устройством (ЗУ). Скользящий режим обеспечивает робастное управление, позволяющее системе эффек- тивно справляться с неопределенностями и возмущениями, характерными для пневматических систем.
Основная идея метода заключается в том, чтобы заставить систему двигаться по заранее определенной траектории, называемой «поверхностью скольжения» [8] . Когда система попадает на эту траекторию, она начинает «скользить» по ней к нужной цели, игнорируя многие внешние воздействия.
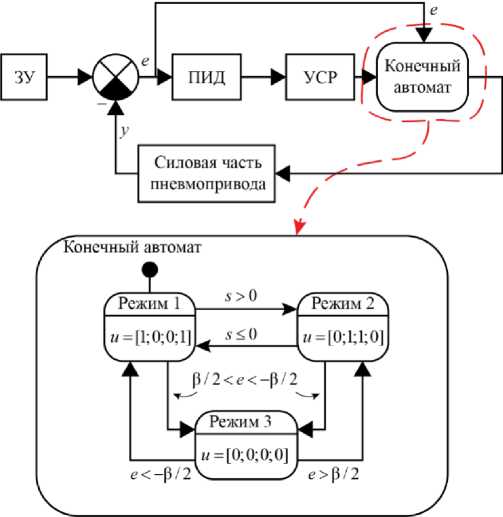
Рис. 2. Структура системы управления
В данной работе используется прямая скольжения, описываемая уравнением:
s = C1 e + C 2 e , где s — функция переключения; e — ошибка регулирования; е — скорость изменения ошибки; C 1 и C2 — положительные коэффициенты, определяющие наклон и характеристики прямой скольжения.
Управление состоит из двух частей: одна часть удерживает систему на нужной траектории, а другая — быстро возвращает ее обратно, если что-то пытается сбить систему с пути [9] . Эта вторая часть может вызывать быстрые нежелательные колебания.
Управляющий сигнал от регулятора скользящего режима подается на вход конечного автомата, формирующего со- ответствующие комбинации управляющих воздействий для пневмораспределителей. Система реализует три основных режима работы: выдвижение поршня (активны Р1 и Р4), втягивание поршня (активны Р2 и Р3) и торможение (активны Р1 и Р2). Режим торможения, при котором давление питания подается в обе полости пневмоцилиндра, включается при достижении ошибки регулирования значений из диапазона [~р/2; +в/2], где в — ширина коридора торможения.
Математическая модель силовой пневматической части включает уравнение динамического баланса сил на поршне пневмоцилиндра, уравнения заполнения и опорожнения полостей пневмоцилиндра и уравнения массовых расходов для нагнетательной и выхлопной полостей [10] .
Р 1 ■ F 1
d 2 y dy ( dy ^
—
Р2 ■ F2 = m—f + D ■ y — + Rтр ■ sign I 1 + Rуп, dt2 dt I dt)
где p 1 , p 2 — давления в поршневой и штоковой полостях пневмоцилиндра; F 1 , F 2 — поршневая и штоковая площади поршня; m — приведенная масса; R тр — сила кулоновского трения; D — коэффициент вязкого трения; R уп — сила реакции упоров в пневмоцилиндре; у — перемещение поршня.
Реакция упоров, ограничивающих перемещение поршня, может быть рассчитана по следующим формулам:
Для случая, когда поршень приближается к нижнему упору (при у < -0,5 H):
R уп = С уп ■ ( у + 0,5 H ) + в уп у .
Для случая, когда поршень находится в пределах рабочего хода (при -0,5 H< у < 0,5 H):
Машиностроение и машиноведение
R уп = 0.
Для случая, когда поршень приближается к верхнему упору (при y > 0,5 H ):
Rуп = Суп ■ (у - 0,5H) + вуп У, где H — ход поршня пневмоцилиндра; Cуп, βуп — коэффициенты жесткости и диссипации контактного взаимодействия поршня пневмоцилиндра с упором соответственно.
Уравнение заполнения и опорожнения левой полости имеет вид [11] :
kR ( T М G 1 - T 1 G 2 ) = kp 1 F 1 У + F 1 ( y w + y ) p 1 , (1)
где k — показатель адиабаты; R — удельная газовая постоянная; Т м , T 1 — температуры воздуха в магистрали и в левой полости пневмоцилиндра; G 1 , G 2 — массовые расходы воздуха через пневмораспределитель Р1 и Р2 соответственно. Величина учитывает выбор начала координат y , а также мертвый объем левой части пневмоцилиндра, включая объем подводящей линии и определяется по выражению:
у 1о = V 0 + 0 , 5 H.
F 1
Массовые расходы G 1 и G 2 для адиабатического процесса рассчитываются по уравнению Сен-Венана – Ванцеля [12] :
G 1
= И f I Р м
2 k
( k — 1) Tи
■ ф ( p м ,p 1 ) ;
G 2 = И f 2 Р 1
2 k
(к — 1) T1
■ ф ( Р 1 ,Р а ) ,
где p м , p a — давления магистрали и атмосферы; μ — коэффициент расхода, f 1 , f 2 — площади дроссельных щелей пневмораспределителей Р1 и Р2 соответственно.
Расходная функция φ( p a , p b ) для двухатомного идеального газа определяется следующим образом
При докритическом режиме истечения (когда p a / p b > 0,528):
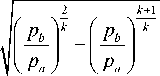
При критическом и сверхкритическом режиме истечения (когда p a / p b ≤ 0,528):
ф(Ра , Рь) = 0,259, где k — показатель адиабаты (для двухатомного газа обычно k = 1,4).
Температура Т 1 при адиабатическом процессе опорожнения равна:
к — 1
p k
T 1 = T a Р| . (4)
I Р а J
Подставив (1), (2) и (3) в (4) получим:
(к — 1 ) к — 1
Процессы заполнения и опорожнения правой полости описываются следующим уравнением:
kR ( T m G 4 — T 2 G 3 ) = — кР 2 F 2 y + F 2 ( У 20 — У ) Р 2 , (5)
где T 2 — температура воздуха в правой полости пневмопривода; G 3 , G 4 — массовые расходы воздуха через пневмораспределитель Р3 и Р4 соответственно. Величина y 2 определяется по формуле:
у 20 = V 20 + 0 , 5 H.
F 2
В выражении V 20 — мертвый объем правой полости гидроцилиндра, включая объем выхлопной линии. Температура T 2 при адиабатическом процессе опорожнения равна:
к — 1
T (Р 2 ^ k 1 2 = T a
.
I Ра J
Массовые расходы G 3 и G 4 равны:
G i = И f i P м
2 k
( k -№ Ф ( P м^ ;
G 2 = И f 2 P ij ,t2 ~ Ф ( P 1 ,P а ) , \( k - 1 ) T i
где f 3 , f 4 — площади дроссельных щелей пневмораспределителей Р3 и Р4 соответственно.
Подставив (6), (7) и (8) в (5) получим:
F 2 ( У 20 - У ) p 2 = g ( f 4 ,f 3 ,P 2 ) + kP 2 F 2 y.
Представленная математическая модель пневмопривода впоследствии была реализована в программном пакете Matlab Simulink (рис. 3). Численное моделирование системы производилось на основе параметров, значения которых представлены в таблице 1.
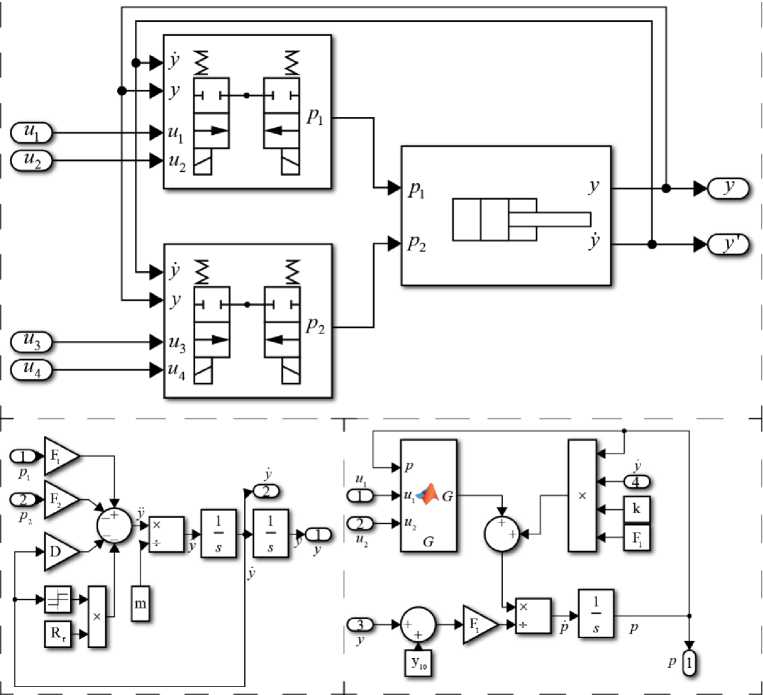
Рис. 3. Модель пневмопривода с дискретными пневмораспределителями в Matlab Simulink
Значения параметров модели для численного моделирования
Таблица 1
|
Параметр |
Значение |
|
Приведенная масса на конце штока, кг |
6 |
|
Давление магистрали, бар |
4 |
|
Давления выхлопа, бар |
1 |
|
Диаметр поршня пневмоцилиндра, мм |
32 |
|
Диаметр штока пневмоцилиндра, мм |
12 |
|
Температура рабочей среды, K |
293,15 |
|
Сила трения страгивания, Н |
20 |
|
Сила трения скольжения, Н |
15 |
|
Коэффициент вязкого трения, мм/с |
350 |
Машиностроение и машиноведение
Предлагаемая методика построения множества Парето для рассматриваемой структуры пневмопривода представлена в виде алгоритма на рис. 4 и включает несколько этапов.
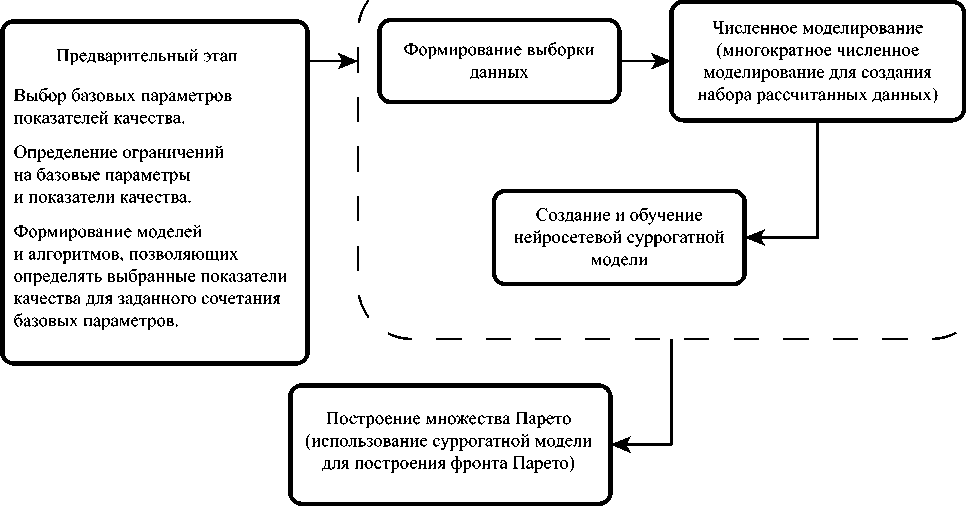
Рис. 4. Алгоритм построения множества Парето
Выбор базовых параметров показателей качества.
Определение ограничений на базовые параметры и показатели качества.
Формирование моделей и алгоритмов, позволяющих определять выбранные показатели качества для заданного сочетания базовых параметров.
Численное моделирование (многократное численное моделирование для создания набора рассчитанных данных).
Создание и обучение нейросетевой суррогатной модели.
Построение множества Парето (использование суррогатной модели для построения фронта Парето).
На предварительном этапе выбираются показатели качества, оценивающие совершенство исследуемой системы. Для комплексной оценки качества переходного процесса может быть использована обобщенная интегральная квадратичная оценка [1] :
«
J 21 = j[ e2 (t) + t e (t)] dt, где e — переходная составляющая ошибки, нормированная от 0 до 1; τ — весовой коэффициент.
Улучшение качества переходного процесса связано с увеличением числа переключений пневмораспределителей n . В этой связи представляет интерес исследование предельных возможностей рассматриваемой структуры пневмопривода по двум конфликтующим показателям качества J 21 и n . На предварительном этапе выбираются показатели качества, которые оценивают эффективность исследуемой системы. Таким образом, формируется пространство показателей качества, в котором будет выделена поверхность, соответствующая фронту Парето.
Из конструктивных параметров системы выделена группа базовых параметров, определяющих основные характеристики управления: коэффициенты наклона прямой скольжения C 1 и C 2 , время срабатывания распределителей и ширина коридора торможения. Диапазоны варьирования этих параметров определяют пространство поиска оптимальных решений и представлены в таблице 2.
Интервалы значений варьируемых параметров
Таблица 2
|
Коэффициент С 1 |
1,0–4,0 |
|
Коэффициент С 2 |
0,1–1,0 |
|
Время срабатывания распределителя, мс |
5–45 |
|
Величина коридора торможения, мм |
2–4 |
Для расчета вектора показателей качества по вектору базовых параметров формируются соответствующие модели. Для рассматриваемого случая использовалась нелинейная динамическая модель, включающая в себя как силовую пневматическую часть, так и систему управления на базе скользящих режимов.
На следующем этапе пространство параметров заполняется расчетными точками, в которых будет вычисляться вектор показателей качества. При этом количество точек должно быть минимальным для сокращения вычислительных затрат, но достаточным для обеспечения необходимой точности суррогатной модели. Важным требованием является также равномерность распределения точек в пространстве параметров.
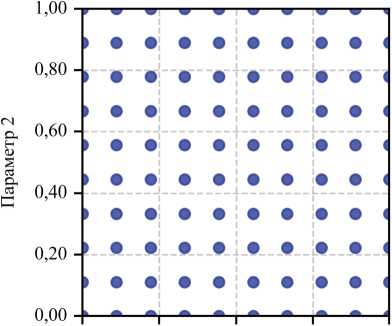
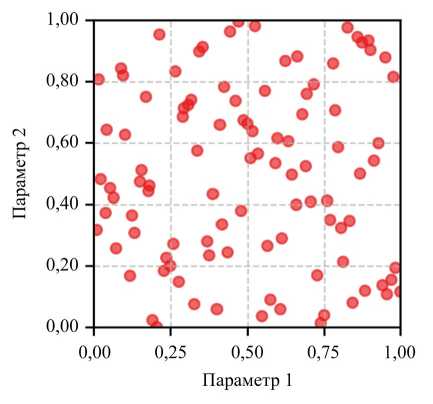
Для построения суррогатной модели были исследованы различные методы заполнения пространства параметров: случайная выборка, метод латинского гиперкуба (ЛГК), метод Соболя и сеточный метод. На рис. 5 представлено сравнение заполнения двумерного пространства равномерным методом прямого перебора и методом ЛГК. Несмотря на кажущуюся визуальную равномерность, прямой перебор обеспечивает худшее качество заполнения по сравнению с методом ЛГК.
0,00 0,25 0,50 0,75 1,00
Параметр 1
а)
б)
Рис. 5. Заполнение пространства параметров расчетными точками: а — равномерное заполнение; б — заполнение методом ЛГК
Для количественной оценки равномерности покрытия пространства параметров был разработан метрический метод [2], основанный на сравнении удельного среднего расстояния между соседними точками. Метод включает нормализацию параметров в единичном гиперкубе, генерацию точек исследуемым методом заполнения и расчет коэффициента Монте-Карло. Этот коэффициент представляет собой отношение фактического среднего расстоя- ния между соседними точками к ожидаемому среднему расстоянию:
I =
0 , 5
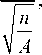
Машиностроение и машиноведение
где n — количество реальных точек; A — площадь области (в рассматриваемом случае A = 1).
Для выбранных сочетаний параметров были проведены параллельные расчеты модели и вычисления показателей качества, что позволило сформировать набор данных для построения суррогатной модели. В работе использована нейронная сеть прямого распространения следующей архитектуры [3, 13] : входной слой (3 входа с нормализацией данных), два полносвязных слоя (16 и 8 нейронов) с функциями активации ReLU, выходной слой для регрессии. Обучение сети проводилось с использованием алгоритма ADAM, обеспечивающего адаптивную настройку скорости обучения и эффективную работу с зашумленными данными.
На заключительном этапе построение границы Парето осуществлялось с помощью эволюционного алгоритма NSGA-II [4, 14] , использующего полученные с помощью суррогатной модели оценки показателей качества. Данный алгоритм позволяет эффективно выявлять множество недоминируемых решений в пространстве критериев качества [15] .
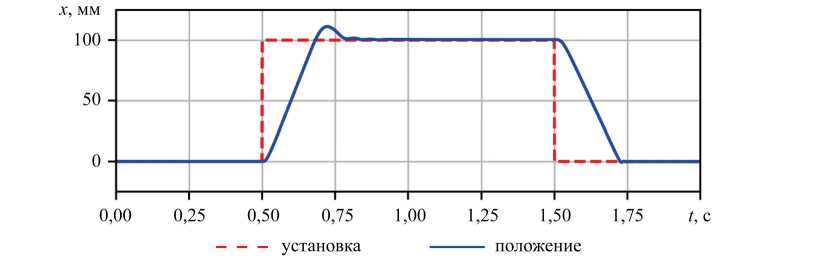
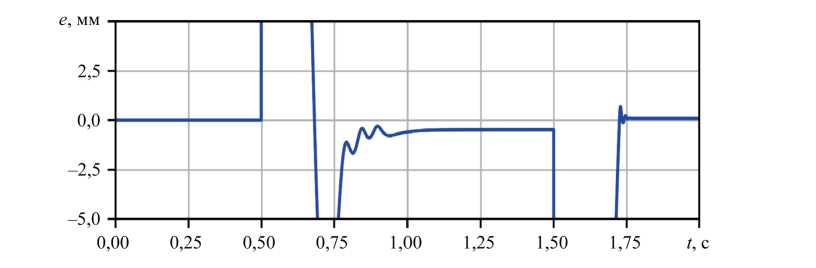
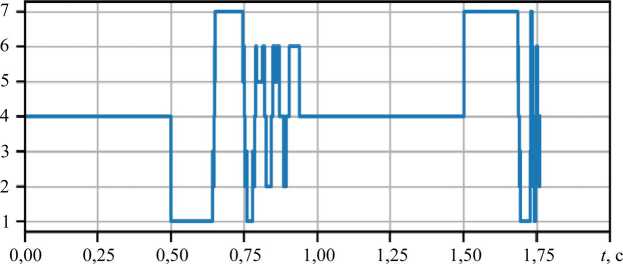
Результаты исследования. Разработанная методика была апробирована на позиционном пневмоприводе с дискретными распределителями. На первом этапе было проведено исследование динамических характеристик системы управления. На рис. 6 представлены переходные процессы, демонстрирующие основные особенности функционирования привода. Анализ графиков показывает симметрию в количестве переключений управляющего сигнала при прямом и обратном ходе, что свидетельствует о стабильности алгоритма управления. При этом наблюдается асимметрия точности позиционирования: для прямого хода системы ошибка регулирования достигает 1,5 мм, что объясняется конструктивными особенностями одноштокового пневмоцилиндра.
в)
Рис. 6. Переходные процессы пневмопривода с дискретными пневмораспределителями: а — переходной процесс; б — ошибка регулирования; в — переключение режимов
Оценка влияния параметров системы на переходные процессы выявила, что уменьшение ширины коридора торможения повышает точность позиционирования, сопровождаясь увеличением числа переключений пневмораспределителей. Аналогичным образом увеличение быстродействия пневмораспределителей повышает точность позиционирования, но приводит к усилению колебательности переходного процесса и увеличению числа переключений. При этом величина перемещения не оказывала значимого влияния на характер переходного процесса, что свидетельствует о линейности системы в широком диапазоне рабочих перемещений и подтверждает эффективность алгоритма управления.
При построении суррогатной модели область параметров была заполнена расчетными точками, при этом предпочтение было отдано методу латинского гиперкуба, который обеспечивает равномерное распределение точек по сравнению с прямым перебором, случайной выборкой, методом Соболя и сетевым методом. Расчёт коэффициента Монте-Карло (таблица 3) продемонстрировал, что метод латинского гиперкуба характеризуется наименьшей дисперсией расстояний между соседними точками, что позволило сформировать выборку из 2 500 комбинаций базовых параметров. Применение замещающих суррогатных моделей снизило трудоёмкость построения множества Парето, что отразилось на уменьшении времени расчёта на 48 %. Суррогатная модель была построена на основе нейросетевых технологий, при этом анализ различных подходов к формированию обучающей выборки данных подтвердил целесообразность использования метода латинского гиперкуба.
Таблица 3
Сравнение равномерности покрытия пространства параметров различными методами выборки
|
Метод выборки |
Коэффициент Монте-Карло |
|
Случайная выборка |
1,024 |
|
Метод латинского гиперкуба |
0,997 |
|
Метод Соболя |
0,980 |
Для каждой комбинации базовых параметров был выполнен расчёт математической модели с определением показателей качества, что позволило рассматривать совокупность расчётных точек каждой итерации алгоритма как поколение. В рамках процедуры недоминирующей сортировки выделялись неулучшаемые решения, формирующие фронт Парето нулевого ранга, а оставшиеся точки образовывали фронт Парето первого ранга. Последующая генерация следующего поколения осуществлялась посредством операций, аналогичных скрещиванию, мутациям и отбору, при этом фиксированный размер поколения поддерживался посредством отсечения наименее качественных вариантов. Алгоритм оптимизации завершался при достижении максимального числа поколений или требуемого уровня сходимости. Результатом работы алгоритма, реализованного с использованием эволюционного алгоритма NSGA-II, стала граница Парето, представленная на рис. 7, отражающая неулучшаемые решения с балансом между числом переключений пневмораспределителей и качеством переходного процесса. При этом небольшая крутизна границы позволяет существенно уменьшить количество переключений без значительного ухудшения переходных характеристик.
Использование нейросети с четырьмя скрытыми промежуточными слоями и обучающей выборкой, состоящей из 2500 точек, позволило обеспечить среднюю точность замещающей суррогатной модели равной 91 %, при этом максимальное отклонение составило 12 %. Дополнительное увеличение числа точек на 50 % привело к росту точности замещающей модели на 15 %.
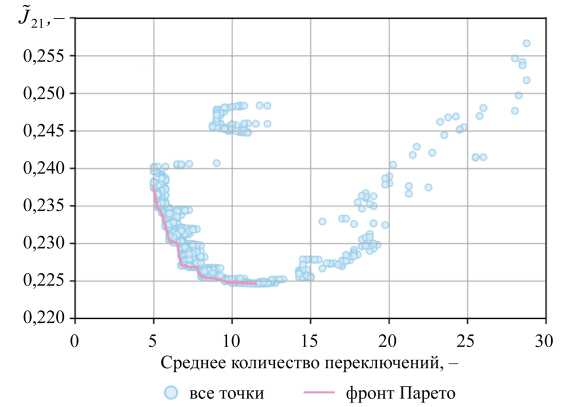
Рис. 7. Множество Парето для пневмопривода с дискретными распределителями
Машиностроение и машиноведение
Обсуждение и заключение. Полученные результаты свидетельствуют о высокой стабильности алгоритма управления, обеспечивающего симметричное переключение сигналов при прямом и обратном ходах, что подтверждает корректность применённого подхода к управлению пневмоприводом. Выявленная асимметрия точности позиционирования, выражающаяся в ошибке до 1,5 мм для прямого хода, указывает на необходимость дальнейшей оптимизации конструктивных особенностей пневмоцилиндра.
Анализ влияния параметров системы на динамические характеристики продемонстрировал, что компромисс между точностью позиционирования и числом переключений пневмораспределителей требует оптимального выбора ширины коридора торможения и быстродействия распределителей. Использование метода латинского гиперкуба для формирования обучающей выборки обеспечило равномерное заполнение параметрического пространства, что подтверждено расчётами коэффициента Монте-Карло.
Применение замещающих суррогатных моделей, построенных на основе нейросетевых технологий, позволило снизить трудоёмкость построения множества Парето и сократить время расчёта на 48 %, что свидетельствует о перспективности данного подхода в задачах оптимизации. Эффективность эволюционного алгоритма NSGA-II, используемого для построения границы Парето, подтверждена получением компромиссных решений, обеспечивающих баланс между числом переключений пневмораспределителей и качеством переходного процесса.
Достижение средней точности замещающей модели на уровне 91 % и уменьшение максимального отклонения до 12 % при использовании нейросети с четырьмя скрытыми слоями демонстрируют высокую эффективность нейросетевых технологий, а увеличение точности на 15 % при расширении обучающей выборки на 50 % указывает на потенциал дальнейшего повышения точности моделей.
Таким образом, результаты проведённых исследований подтверждают потенциал предложенной методики для повышения эффективности позиционных пневмоприводов с дискретными распределителями и определяют перспективные направления дальнейших оптимизационных исследований в данной области.


