Использование связанных фотонно-кристаллических резонаторов для повышения чувствительности оптического датчика

Разработка датчиков показателя преломления материалов на основе оптических микрорезонаторов привлекает большое внимание [1]. Такие датчики используются, например, в биологических [2] и химических [3] исследованиях, при измерениях температуры, механического напряжения, в акустике. Достигнуты величины добротности оптических резонаторов на уровне 106 и выше. Данные значения добротности могут быть увеличены путём использования активных резонаторов [4] с оптической или электронной накачкой. Столь большие величины добротности оптических резонаторов обеспечивают датчикам на их основе высокую чувствительность.

Кроме этого, особенности функционирования резонансных датчиков допускают возможность получения динамического отклика в режиме реального времени. Также допускается использование широкого диапазона исследуемых образцов. Это могут быть, например, различные химические соединения в жидкой и газообразной форме или исследуемые биомолекулы. Оптические резонансные датчики демонстрируют хорошую совместимость с требованиями мик-рофлюидики. Это делает их хорошими кандидатами для использования в составе интегрированных решений в виде биочипов или «лаборатории на кристалле» ( lab-on-a-chip ). Ещё одним преимуществом оптических резонансных датчиков по сравнению с традиционными датчиками является то, что устраняется необходимость в использовании флуоресцентных меток.

Существуют примеры использования различных видов оптических резонаторов в датчиках показателя преломления. Например, были предложены датчики на основе сферических резонаторов [5]. Дисковые резонаторы в качестве компонентов оптических датчиков рассмотрены в работе [6].

Датчики показателя преломления на основе кольцевых резонаторов [7] являются, пожалуй, наиболее распространённым решением. Они легко интегриру- ются на кристалле, и для них существуют отработанные технологии изготовления. Оптические датчики на основе фотонно-кристаллических резонаторов рассматриваются, в частности, в работе [8].

В оптических датчиках, как правило, свет подаётся в резонансную камеру через одномодовый волновод. Спектр пропускания резонатора имеет форму кривой Лоренца. Кривизна склона этой кривой зависит от величины добротности резонатора и определяет чувствительность датчика.

Оптические датчики на основе кольцевых резонаторов более компактны, чем, например, датчики на основе сферических или дисковых резонаторов. Их размеры составляют десятки микрометров по обоим направлениям плоскости кристалла.

Предлагаемые в данной работе решения демонстрируются на наиболее компактных на сегодняшний день оптических датчиках показателя преломления материалов на основе фотонно-кристаллических резонаторов (ФК) [9, 10]. Их размеры, как правило, не превышают величины нескольких длин волн используемого света.

1.    Постановка задачи

На рис. 1 показана предлагаемая схема оптической системы из двух связанных резонаторов. Фазовая задержка связи резонаторов составляет величину θ . Здесь переменные κ j , j = {1, 2}, обозначают коэффициенты связности j -го резонатора с волноводом, r j , j = {1, 2} – коэффициенты энергетических потерь j -го резонатора в пространство, p in , p rf , p tr – амплитуды входного, отражённого и прошедшего полей соответственно.

Рис. 1. Схема оптической системы из двух связанных с фазовой задержкой резонаторов

Согласно временной теории связанных мод (CMT) [11], функцию пропускания одного резонатора можно записать в виде

2к                                 r ,

Ti ( Sj ) =---- j -, Sj= i ( «-« j + j j = { 1,2 } , (1)

sj + 2k j где «j, j = {1,2} - резонансная частота j-го резонатора. Добротность j-го резонатора Qj определяется соотношением 1/Qj = 1/Qjк +1/Qjr, где Qjк = «Z(4xj) и Qjr = «/(2j

		/ / / /	X \ \
		/	\		VMKM

1,48796 1,48798 1,48800 1,48802 1,48804

Рис. 2. Функции пропускания одного резонатора (штриховая линия) и двух связанных резонаторов при 9 = П2 (сплошная линия)

Функция пропускания системы из двух резонаторов, которая изображена на рис. 1, при 6 = п/2 записывается в виде

T2 (s )=     '     ^( S + ко ) +к1

.

Дисперсией волновода мы здесь пренебрегаем. Набег фазы 6 = п /2 соответствует ситуации, при которой связывающий волновод отсутствует.

На рис. 2 показаны штриховой линией функция пропускания одного резонатора согласно формуле (1) и сплошной линией функция пропускания двух таких же связанных резонаторов согласно формуле (2). Видно, что использование двух резонаторов вместо одного позволяет повысить добротность системы. Добротность системы с одним резонатором составила Q 1 = 1,5 ^х 10⁵, резонансная длина волны % ₀ = 1,488 мкм. Внешние потери данного резонатора определяются величиной Qj_r =2,5× 10⁵.

2.    Расчёт оптической системы на основе связанных фотонно-кристаллических резонаторов

В качестве конкретного ФК-резонатора рассчитаем резонатор на основе двумерного гребенчатого ФК-волновода. Такие резонаторы обладают малой площадью и естественным образом интегрируются в волноводную геометрию соединений на кристалле. На рис. 3 а показан резонатор на основе гребенчатого ФК-волновода. Дефект, в котором возбуждается резонансная мода, формируется уменьшением радиуса отверстий в окрестности резонансной камеры.

На рис. 3б приведены геометрические параметры отверстий в окрестности резонансной камеры. Эти геометрические параметры обеспечивают для заданной длины волны света возникновение энергетиче- ской запрещённой зоны (bandgap) для TE-поляризации в волноводе.

а)

б)

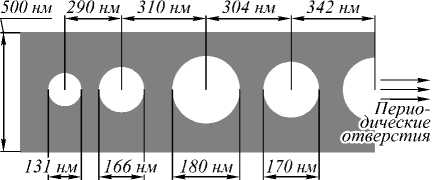
Рис. 3. Резонатор на основе гребенчатого ФК-волновода в кремнии (а), геометрические параметры резонансной камеры (б)

Для расчёта характеристик резонатора использовался двумерный метод FDTD [12]. Волновод имеет ширину w = 500 нм и состоит из материала с показателем преломления, равным 2,97. Такая величина соответствует эффективному показателю преломления волновода из кремния толщиной 270 нм, который лежит на стеклянной подложке и окружён воздухом.

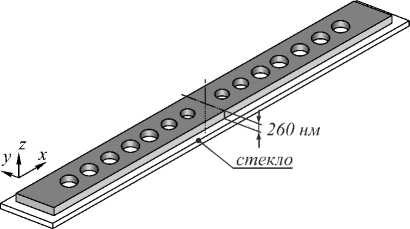
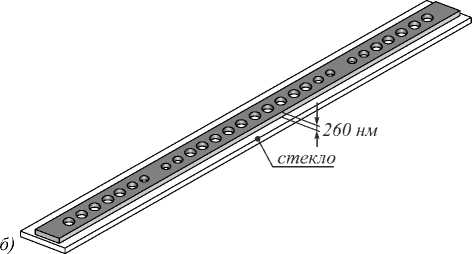
Рис. 4. Пример трёхмерного резонатора с тремя регулярными отверстиями на основе ФК-волновода на подложке (а), система, состоящая из двух связанных трёхмерных резонаторов (б)

На рис. 4а изображён трёхмерный резонатор с тремя регулярными отверстиями на основе ФК-волновода на подложке. На рис. 4б показана система из двух таких резонаторов. Отверстия в регулярной части волновода заполнены воздухом, имеют диаметр 185 нм и отстоят друг от друга на a = 350 нм. Длина волны резонансной моды равна 1488,27 нм. Добротность одного резонатора с 8 регулярными отверстиями с каждой стороны равна 156413. Внешние потери данного резонатора определяются величиной Qjr = 2,56× 105. Эти величины примерно соответству- ют параметрам резонатора, функция пропускания которого изображена на рис. 2.

3.    Результаты вычислительного эксперимента

На рис. 5 показаны отсчёты функции пропускания для систем из одного и двух резонаторов. Отсчёты функции рассчитаны с использованием метода FDTD. Параметры базового резонатора соответствуют параметрам, которые приведены на рис. 4 б . Видно, что кривые на рис. 5 соответствуют кривым на рис. 2 с

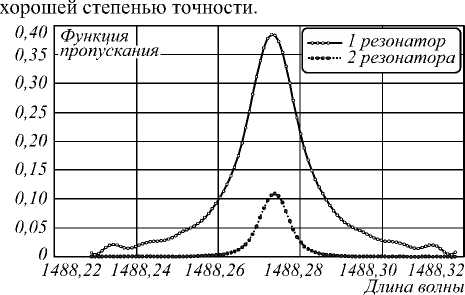
Рис. 5. Отсчёты функции пропускания одного (интерполированы точечной линией) и двух (интерполированы сплошной линией) резонаторов, рассчитанные методом FDTD

На рис. 6 показаны функции пропускания для систем из двух резонаторов, рассчитанные аналитически (сплошная линия) и методом FDTD (отсчёты интерполированы точечной линией). Период регулярной части ФК-волновода составляет 350 нм. Поэтому отсутствие связывающего волновода ( θ = π /2) соответствует значению d = 350 нм. Однако на рис. 6 видно, что почти полное соответствие между кривой, заданной аналитическим выражением (2) при θ = π /2, и результатом FDTD-моделирования достигается при d = 354 нм. Это может быть объяснено тем, что брэгговская частота фотонно-кристаллического волновода не совпадает с резонансной частотой. В этом случае, чтобы реализовать условие θ = π /2, требуется добавить фрагмент волновода между резонаторами [3].

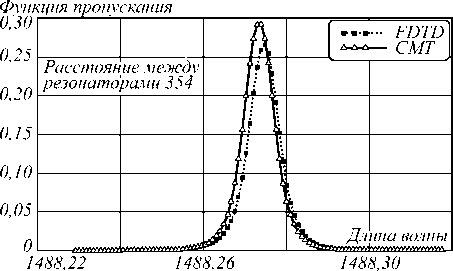
Рис. 6. Функции пропускания для систем из двух резонаторов при θ = π/2, рассчитанные при помощи теории связанных мод (сплошная линия) и методом FDTD (отсчёты интерполированы точечной линией)

Чувствительность резонансной системы может быть наглядно оценена крутизной склона спектраль- ного пика. Например, в датчиках показателя прелом- ления крутизна склона спектрального пика соответствует скорости изменения функции пропускания при изменении показателя преломления окружающей среды. На рис. 7 показаны производные спектральных пиков функций пропускания систем из одного (точечная линия) и двух (сплошная линия) резонаторов, полученные FDTD-моделированием.

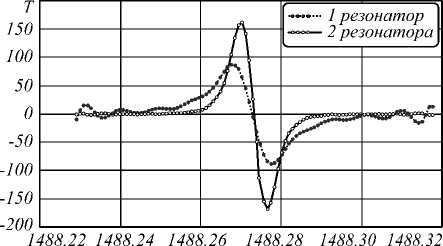
Длина волны

Рис. 7. Производные спектральных пиков функций пропускания систем из одного (точечная линия) и двух (сплошная линия) резонаторов

Из рис. 7 видно, что максимальное значение производной спектрального пика функции пропускания для системы из двух связанных резонаторов примерно в два раза больше соответствующего значения для одного резонатора. Это приводит к лучшей чувствительности системы из двух резонаторов по сравнению с одним резонатором. Для используемых параметров резонаторов это улучшение чувствительности достигается, однако, увеличением требуемого уровня энергии входного сигнала, что можно видеть на рис. 5. Тем не менее, очевидные аналитические расчёты показывают, что различие между максимумами функций пропускания одного и двух резонаторов может быть уменьшено путём сокращения внешних энергетических потерь. Например, для Q 1 = 1,5×10⁵ и Q jr =2,5×10⁶ это различие составляет 3 %.

4.    Численный анализ погрешностей изготовления резонаторов

С помощью численного моделирования покажем, как погрешности при изготовлении одинарных и связанных резонаторов влияют на смещение частот резонансных мод резонаторов и на добротность резонансной системы.

В табл. 1 приведены результаты моделирования влияния погрешностей изготовления одного ФК-резонатора. Варьировались радиусы отверстий в ФК-волноводе. Погрешность радиуса каждого отверстия полагалась случайным числом, которое равномерно распределено в интервале ±1, ±2, ±3, ±4 или ±5 нм. Столь упрощённая схема моделирования влияния погрешностей изготовления обусловлена, прежде всего, тем, что расчёт характеристик одного резонатора методом FDTD занимает несколько часов машинного времени на вычислительном кластере пиковой мощностью 1 ТФлопс. Из табл. 1 видно, что при погрешности ±5 нм сдвиг резонансной частоты может достигать 3 нм. При этом с ростом погрешности значение добротности резонатора может как уменьшиться, так и увеличиться.

Табл. 2 демонстрирует результаты моделирования влияния погрешностей изготовления системы из двух связанных ФК-резонаторов. Здесь изменения функции пропускания обусловлены, прежде всего, рассогласованием двух резонаторов по резонансным длинам волн. При таком рассогласовании резонансные моды резонаторов перестают быть вырожденными, что приводит к уширению спектрального пика функции пропускания.

Табл. 1. Значения резонансной длины волны и добротности при различных величинах погрешности для системы из одного ФК-резонатора

Погрешность, нм	Длина волны, нм	Добротность
±0	1488,2	156413
±1	1488,2	156435
±2	1488,3	153050
±3	1489,2	183318
±4	1490,7	110346
±5	1491,2	97482

Табл. 2. Значения резонансной длины волны и добротности при различных величинах погрешности для системы из двух связанных ФК-резонаторов

Погрешность, нм	Длина волны, нм	Добротность
±0	1488,2	252739
±1	1487,1	172461
±2	1484,8	110686
±3	1483,6	312560
±4	1482,8	180881
±5	1482,5	297793

Таким образом, индивидуальная подстройка резонансной длины волны каждого резонатора позволит хотя бы частично компенсировать невырожденность резонансных мод. Динамическая подстройка резонансной длины волны каждого резонатора может быть реализована изменением показателя преломления волновода. Для этого может быть использован, например, эффект Керра, инъекция свободных носителей ( free carriers ) или температурное воздействие. Среди этих способов температурное воздействие допускает реализацию на наименьшей частоте. Однако для описанной здесь резонансной системы высокая скорость изменения резонансной длины волны не требуется.

В последнее время в качестве способа изменения показателя преломления в ФК-резонаторе часто используется инъекция свободных носителей. Возможны оптическая или электронная накачки свободных носителей в ФК-резонатор. Если сравнивать с оптической накачкой, то возможность электронной накачки рассмотренного резонатора обеспечивает способы практи- ческой реализации предложенного в данной работе устройства.

Заключение

В работе рассмотрен способ двукратного повышения добротности оптической резонансной системы. Рассчитано устройство на основе одного и двух связанных фотонно-кристаллических резонаторов. Показано хорошее соответствие между аналитическим и численным моделированием. Исследованы допуски погрешностей изготовления предложенного устройства на основе фотонно-кристаллических резонаторов. Предложены методы компенсации погрешностей изготовления предложенного датчика.

Работа выполнена при поддержке грантов РФФИ №№ 13-07-97002, 13-07-13166, 14-07-97008, 14-0797009, Программ №№ 2 и 5 фундаментальных исследований ОНИТ РАН и Министерства образования и науки РФ.