Использование теории кубатурных формул в задачах автоматического управления

Методы решения задач синтеза управляющих воздействий для динамических систем в настоящее время представлены в широком спектре работ по теории управления, обзор современного состояния которого достаточно полно представлен в [1]. Однако в практическом приложении это многообразие методов редко позволяет достаточно просто и в то же время достаточно точно построить управление в конечной, аналитической форме.

В классическом представлении математическая модель линейной стационарной системы может быть записана в виде векторного уравнения х (t) = A • x (t) + B • u (t), (1) где x(t) = {xi (t)} - и-мерный вектор состояния системы; u (t) = {u j (t)} - /-мерный вектор управления; A = {aij}, (i, j = 1,n ) и B = {j, (i = 1,n , j = 1,/)- матрицы коэффициентов системы.

Постановка задачи управления: перевод системы из заданного начального состояния { x ⁰ } в заданное конечное состояние { x k } за определенный интервал времени Т.

Введем в рассмотрение множество функций - полиномы Эйлера { E s ( t ) } ( s = 1, ^ ), составляющие базис в функциональном пространстве координат состояния и управления. Полиномы Эйлера для ( s = 1, m ) определяются выражениями [2]

E ⁽ t ) = t - 2,

E , ( t ) = t ² - 1 ,

.

E_m ( t ) =

(1 - t ) m ^{+ 2} ( td 1 m ^] t ^ dt J

t

' '

Умножим каждое из уравнений системы (1) на одну из первых (m -1) функций данного множества и получим семейство (m -1) систем вида л.1 (t) • E1 (t) = au • x1 (t) • E1 (t) + a12 • x2 (t) x XE1(t) + ... + a1 n • xn (t) • E1(t) + +bu • u1( t) • E1( t) + b12 • u 2( t) x xE1(t) +... + b l • ul(t)• E1(t);

j2 (t) • E1 (t) = a 21 • x1 (t) • E1 (t) + a 22 x xx2(t)• E1 (t) +... + a2n • xn(t)• E1 (t) +

+ b ₂₁ • u 1 ( t ) • E 1 ( t ) + b ₂₂ • u ₂ ( t ) x x E 1 ( t ) + ... + b ₂ l • u l ( t ) • E 1 ( t );

^x n ⁽ t ) • ^E 1 ⁽ t ) = ^an 1 • ^x 1 ⁽ t ) • ^E 1 ⁽ t ) ^{+ a}n 2 ^x x x 2 ⁽ t ) • E 1 ⁽ t ) + ... + ^ann • x n ⁽ t ) • E 1 ⁽ t ) + + b n 1 • u 1 ⁽ t ) • E 1 ⁽ t ) + b n 2 • u 2 ⁽ t ) x x E 1 ( t ) + ... + b_nl • u l ( t ) • E 1 ( t );

% 1 (t) • E2 (t) = an • x1 (t) • E 2 (t) + a12 x xx2(t) • E2(t) +... + a1 n • xn(t)• E2(t) + +b11 • u1 (t) • E2 (t) + b12 x x u2 (t) • E2 (t) +... + b1 l • ul (t) • E2 (t); x 2 (t) • E 2 (t) = a 21 • x1 (t) • E 2 (t) + a 22 x x x2(t)• E2(t) +... + a2n • xn(t) • E2(t) + +b21 • u1 (t) • E2 (t) + b22 • u 2 (t) x xE2(t) +... + b2l • ul(t) • E2(t);

^Xn ⁽ t ) • ^E 2 ⁽ t ) = ^an 1 • x 1 ⁽ t ) • ^E 2 ⁽ t ) ^{+ a}n 2 ^x x x 2 ( t ) • E 2 ( t ) + ... + a nn • x n ( t ) • E 2 ( t ) + + b n 1 • u 1 ⁽ t ) • E 2 ⁽ t ) + b n 2 x x u ₂ ( t ) • E ₂ ( t ) + ... + b_nl • u l ( t ) • E ₂ ( t );

X1 (t) • Ek (t) = a11 • x1 (t) • Ek (t ) + a12 x x x2(t) • Ek(t) +... + a1 n • xn(t) • Ek(t) +

+b11 • u1( t) • Ek (t) + b12 • u1( t) x xEk(t) +... + b11 • ui(t) • Ek(t);

%2 (t) • Ek (t) = a 21 • x1 (t) • Ek (t) + a 22 • x2 (t) x xEk(t)+...+ a2n • xn(t) • Ek (t)+

+b21 • u1 (t) • Ek (t) + b22 • u 2 (t) x xEk(t) +... + b2l • ul(t) • Ek(t);

...                                     (2)

Xn (t) • Ek (t) = an 1 • x1 (t) • Ek (t) + an 2 • x2 (t) x xEk(t) +... + ann • xn (t) • Ek (t) +

+ b n 1 • u 1 ⁽ t ) • E k ⁽ t ) + b n 2 • u 2 ⁽ t ) x ^{x E}k ⁽ t ) ⁺ ... ⁺ b nl • u l ⁽ t ) • ^Ek ⁽ t ).

Проинтегрируем правые и левый части уравнений (2) на интервале [ t 1 , t_m ] ,где t 1 - момент времени, соответствующий исходному состоянию системы; t_m -моментвремени, соответствующий конечной точке фазовой траектории:

J \(t)• Es(t)dt = j^^aiif xj(t)• Es(t)dt + t                                  t, j=i tm '                                                (3)

+ JX b j - u j ( t ) • E s ( t )dt .

1 1 j = 1

Используя свойство интегрирование по частям и соотношение для полиномов Эйлера •

^Es ⁽ t ) = ^sEs - 1 ⁽ t ) ^, преобразуем левую часть выражения (3) к виду

( b n ^1 ^1 ⁽ t 1 )   ...    ^b _n ■ ^cm -E 1 ⁽ t m ) )( u l )

+

...

...

...

■

...

•

tm

tm

'

b n l ^ c l ^ ^En ⁽ t l ) ...    b n l ^ c m ^ ^En ⁽ t m )

I uml J

J x i ( t ) ■ E_s ( t ) dt = J [ x i ( t ) xx E_s ( t ) ] dt -

Используя понятие блок-матрицы, запишем (4) в виде следующего матричного уравнения:

tl

t 1

- J X i ( t ) ■ E s ( t ) dt = t l

= - X i ( t l) E s ( t l ) + X i ( t m ) X

^{X E}s ⁽ t m ) ^- s J x i ⁽ t ) • ^Es - 1 ⁽ t ) ^dt ^

t 1

Рассмотрим на интервале [ t ₁ , t_m ] конечный набор фиксированных моментов времени { t_k }, ( k = 1, m ) и правую часть (3) в соответствии с теорией кубатурных формул (ТКФ) [3] заменим на сумму вида

IL 1L^aj ^^^(tt k ) ■ E s ⁽ t k ) ⁺

( y l

\

2.. m

= ( D l   D 2 )L ¹

I Y 2.. m

+ F ^ u , (5)

где ^ =

...

yn

- и -мерный вектор начального состояния

( У п + 1 )

системы; Y 2. _m =

...

- ( mn - n ) -мерный вектор неиз-

^ ymn j вестных значений координат системы-

Матрицы в уравнении (5) запишем выражениями

lm

+ LL b j ■ C k ■ U j (t k ) ■ E s ( t k ) , j = 1 k = 1

где c_k - коэффициенты кубатурной формулы; E s ( t k ) -значение базисных функции в точке t k ; x j ( t k ) , u j ( t k ) -дискретные значения координат состояния и управления-

Коэффициенты c k должны удовлетворять системе соотношений вида

	(- E 1 ( t l )	0...	...0...	...0...	...0
Z 1 =	0 ...	- E 1 ( t l ) ...	0... ...	...0... ...	...0 ...
	0... V	...0...	...0	- E s ( t l )	...0

;

\

t m                 m

J E i ( t ) dt = L C k ■ E ( t k ), i = 1, 2, 3, ...

.

	( 0...	E 1 ( t m )	...0...	...0...	...0 '
Z 2 =	0... ...	...0 ...	E 1 ( t m ) ...	...0... ...	...0 ...
	0... V	...0...	...0...	...0	E s ( t m ) j

;

c l ■ [ a ll ■ ^E 1 ⁽ t l ) ⁺ E 0 ⁽ t l )]

c l ■ a l n ■ ^E 1 ⁽ t 1 )

.

. I

■ .

.

. I

■ .

.

t l

k = 1

В соответствии с этими преобразованиями запишем систему уравнений (2) в виде:

^- x j ⁽ t l ) ■ ^Es ⁽ t l ) ⁺ x j ⁽ t m ) ■ ^Es ⁽ t m ) =

= У j m L ^aj-^ck- x , -⁽ t k ) ■ ^Es ⁽ t k ) ⁺

D i =

D 2 =

...

^c 1 ■ a n 1 ■ E s ⁽ t l )

c 2 ■ [ a n ■ E l ⁽ t 2 ) ⁺ E o ⁽ t 2 ^)]

. I

■ . I

■ .

.

.

. I

■ .

...

^c r ^{[ a}nn'^E„ ⁽ t l ) ^{+ mE}m - 1 ⁽ t 1 ^)]

c m ■ a l n ■ ^E l ⁽ t m )

;

⁺1L^ck ■ j t k ) ■ sE s - 1 ⁽ t k ) ⁺ k = 1

+ L L b , A ■ U j ( t . ) E ( t k ) - j = 1 k = 1

Введем следующие обозначения:

У 1 = Х 1 ( t l ), y 2 = x 2 ( t l ), y 3 = ^x 1 ⁽ t 2 ),..., y mn = x n ⁽ t m ) u l = u l ⁽ t l ), u 2 = u 2 ⁽ t l ), ..., u ml = u l ⁽ t m )

...

^c 2 ^ n 1 ■ E s ⁽ t 2 )

. I

■ . I

. I

■ .

.

■ .

■ . I

.

...

c \a ■ E (I ) + sE ,U )1 m nn s m s - 1 m

,

где Z _l , Z ₂ , D ₁ , D ₂ - подматрицы, размерность которых определяется размерностью векторов Y и Y_{2 m} ; Z ₁ и D ₁ имеют размерность [ n X m ( n - 1)] ; Z ₂ и D ₂ имеют размерность [ m ( n - 1) X m ( n - 1)] •

Произведем в (5) перегруппировку и получим

( Z 2 - D 2 ) ■ Y 2.. m

^^^^^^s

F ■ u = ( D₁ - Z ₁ ) ■ Y l •

.

В этих переменных система уравнений (2) в матричной форме будет выглядеть следующим образом:

-E l ( t l )       0...

0       - E ₁ ( t ₁ )....

E l ( t m )...0 ) (

0... E l ( t m )...

■

....

....

....

( C l ■ [ a _n ■ E l ( 1 1 ) + E o ( t l )] ...

...

....

y l )

...

^ y mn ^

cm ^ a l n ^ ^E l ⁽ tm )

...

X

с, - а , -Е ил .... с -[а -Е (t )+пЕ .(t )1

1 n 1 n 1 /                      m nn n m          n - 1 m

( yl )

X

...

+

mn

Решая уравнение (5) относительно Y 2 m , можно получить дискретные значения координат траектории движения системы (1) при заданном управляющем воздействии u ( t ) :

Y 2.. m = ( Z 2 - D 2 ) ^{- 1} ■ [( D l - Z 1 ) ^ 1 ! + F ^ u ] , и, в частности, свободное движение, равное

Y 2 = ( Z 2 - D 2 ) ^{- 1} ■ ( D l - Z 1 ) ■ 1 1 •

Эти уравнения можно рассматривать как дискретный аналог непрерывного решения уравнения (1):

x ( t ) = G ( t - 1 ₁ ) ^ x ( t ₁ ) +

+_[G(t -т)^ Вш (t)dт , tl где G(t -т) -матрицант системы (1)-

Аналогично, как было сделано выше, соответствующей перегруппировкой в (4) получим матричное урав-

нение, обусловливающее подобную связь только с конечными координатами Y_m системы:

и окончательно имеем

^^^^^^е

U = [ ( ( S x 1 ) ^{- 1} - ( S xm ) ^{- 1} ) • F ' х

( У 1

^ГД^е Y 1..( m - 1) =

...

стных; У = m

- F • u = ( D 2 - Z 2 ) • Y m ^,

y y n (m-1)+1

...

- ( mn - n ) -мерный вектор неизве-

- и -мерный вектор координат ко

^ y mn , нечного состояния системы.

Произведем группировку подматриц в (6) и (7), выделив в них элементы, соответствующие координатам векторов Y 1 и Y m , для этого представим матрицы ( Z 2 - D 2 ) из (6) и ( Z 1 - D 1 ) из (7) в виде блочных матриц, получаемых следующим образом:

(Z, - D j Y = (S   S )х

2      2    2.. m xm m

2..( m - 1)

m

= X У X У • xm 2..( m - 1) ⁺ mm ^;

( Z 1 - D 1 ) Y ..( m - 1) = ( S 1    s x 1 ) х

х

к

2..( m - 1)

= S 1 Y + Sx ^Лm - 1) ,

где матрицы S x _m и S x 1 имеют размерность [ n ( m - 1) х n ( m - 2)] ; матрицы S_m и S 1 - размерность [ n ( m - 1) х n ] . Преобразуем систему

х .у

^S xm Y 2..( m - 1)

^Sx 1 Y 2..( m - 1)

- F • u = ( D 1 - Z 1 ) • 1 1 - S m • Y m ;

-

F • u = ( D 2 - Z 2 ) • Y m - S • 1 1 ,

\

гд^{е Y} 2..( m - 1) =

- неизвестные значения координат

...

' У. + 1

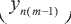
системы.

Умножим слева оба уравнения системы (8) на ( S x _m ) ^{- 1} и ( S x 1 ) ^{- 1} , соответственно, где взятие обратной матрицы понимается в соответствии с [4]:

Y^ m - 1) - ( S xm ) ^{- 1} • F • U = ( S xm ) " X X ( D 1 - Z 1 ) • 1 1 - ( S xm ) ^{- 1} • S m • Y m ;

Y ,.( m - 1) - ( S x 1 ) ^{- 1} • F • U = ( S x 1 ) ^{- 1} х

X ( D 2 - Z 2 ) • Y m - ( S x 1 ) ^{- 1} • S • 1 1

Матрицы в уравнениях системы (9) одинаковой размерности, поэтому можно просуммировать левые и правые части, в результате получим

( ( S x 1 ) ^{- 1} - ( S xm ) ^{- 1} ) • F • U =

= ( ( S xm ) ^{- 1} • ( D 1 - Z 1 ) + ( S x 1 ) ^{- 1} • S 1 ) • 1 1 -

- ( ( S xm ) ^{- 1} • S m + ( S x 1 ) ^{- 1} • ( D 2 - Z 2 ) ) • Y m , ,

_х ( ( S xm ) ^{- 1} • ( D 1 - Z 1 ) + ( S x 1Г¹ • S 1 ) • 1 1 -          _(1O)

"( ( S xm ) ^{- 1} • S m + ( S x 1 ) ^{- 1} • ( D 2 - Z 2 ) ) • 1 _ '

Таким образом, коэффициенты матрицы

[ ( ( S x 1 ) ^{- 1} - ( S xm ) ^{- 1} ) • F J х ( ( S ) ^{- 1} • ( D 1 - Z 1 ) + ( S x 1 ) ^{- 1} • ^S 1 )

представляют ничто иное, как параметры регулятора, где в качестве входного сигнала для регулятора выступает вектор Y = { x ( t 1 )} .

В частном случае, когда речь идет о системе автоматического регулирования и координата x(t) играет роль координаты ошибки, конечное состояние системы соответствует началу координат фазового пространства, тогда вектор управления принимает более простой вид

U =[ ( ( S x 1 ) ^{- 1} - ( S xm ) ^{- 1} ) • F ' х

х[ ( ( S xm ) ^{- 1} • ( D 1 - Z 1 ) + ( S x 1 ) ^{- 1} • S 1 ) • 1 1 ] .

Если число решений в (10) бесконечно, то для выделения единственного решения, естественно, необходимо добавить ограничения на параметры возможной траектории движения, например, зафиксировать ряд промежуточных значений x ( t r ) , где число r можно выбрать таким образом, что матрицы в (10) будут квадратными. Также можно ввести ограничения и на управляющее воздействие. Что касается условия возможности существования единственности решения уравнения (10), то оно является обычным следствием теории линейных алгебраических систем [4].

Используя соотношение (10), можно достаточно просто получить решение и других задач анализа, например, критерий управляемости или наблюдаемости системы (1).

Рассмотренный метод может быть использован для линейных непрерывных систем - как стационарных, так и нестационарных, и позволяет получить закон управления рассматриваемой системы в виде конечного аналитического выражения относительно параметров системы.