Использование вейвлетов для улучшения параметров нейронных сетей в задачах распознавания речи

Проблема интеллектуальности распознающих систем заключается в том, что хотя они уже превзошли человека в точности распознавания, но не могут использовать информацию контекста для более правильной оценки результата, в отличие от человека, для которого задача распознавания речи лишь небольшая часть процесса ее понимания.

Природа речевого сигнала такова, что задачу распознавания речи следует поставить особняком среди других задач распознавания. Прежде всего, следует отметить временную природу сигнала, что отражено в работах [1 -4]. Исследователям приходится учитывать, что речевой сигнал псевдопериодичен,неста-ционарен и имеет части,зависящие от взаимо-положения. Высокая временная вариативность или нестационарность речевого сигнала получила в английских источниках название «Time warping», или искажение времени [1; 4].

Для увеличения интеллектуальности систем автоматического распознавания многим исследователям видится перспективным использовать нейронные сети. Но сложность состоит в том, что классические ИНС плохо приспособлены к работе с сигналами временной природы и локальными искажениями масштаба. Специализированные же ИНС решают эту задачу, но временная вариативность, с которой они могут справиться,низка и ограничена масштабом отдельных звуков и слов.

Одним из способов увеличить эту вариативность является создание гибридных методов. Авторам работы представляется,что наиболее перспективно сочетание ИНС с вейвлет-ана-лизом.

Астапов К.А.

Математическая постановка задачи и модель предлагаемой вычислительной системы

Математическая постановка задачи такова.

Дан ряд x = { x₁ , x₂ , …, x_n }, представляющий отсчеты некоторого сигнала (например, речевого), взятые в соответствии с теоремой Котельникова. Этому ряду сопоставлен ряд p = { p₁ , p₂ , … , p_n }, представляющий собой отсчеты целевой функции, где x ( t ) и p ( t ) – функции от переменной времени t . Требуется построить вычислительную систему, осуществляющую отображение x → p .

В силу изложенных выше соображений, эту вычислительную систему авторам представляется целесообразным строить на основе нейронных сетей и вейвлетов.

Введем условные обозначения, как это показано на рис. 1. Обозначим x_i входные данные, p_i – желаемый результат, y_i – выход нейронной сети, q_i – выход системы (то есть результат обратного вейвлет-преобразования, произведенный над y_i ), E ( w ) – целевая (энергетическая) функция всей системы.

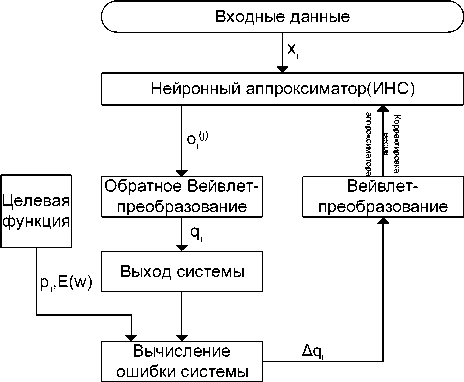
Рис. 1. Условные обозначения

В то же время обратное вейвлет-преобразование можно представить с коннекционистких позиций, как слой нейронной сети. В самом деле, одноуровневая обратная вейвлет-декомпозиция может быть представлена как

N yi')=s (hiV(+1)+gi-2,di+1)), (1)

i - i                                   ¹

где a⁽ l ^{+ 1)} - «грубая» версия сигнала, d i ⁽ l ^{+ 1)} - детализирующие коэффициенты, а ^h i-2i 1 ^{1 и g} i-2i 1 – коэффициенты, характеризующие обратное вейвлет-преобразование.

При этом исходный сигнал может быть представлен последовательным применением формулы (1). Легко увидеть, что если заменить обозначения, введя единую нумерацию для a^{( l + 1)} и d ^{( l + 1)} , обозначив эти значения как x i , i ¹                i i                                                                   ( l + 1)

и так же ввести единые обозначения для ai и d(l+1), обозначив их w, мы получим формулу i1                 (i) 22N i формального yi- = ^ w/x,, что формально соот-i=0

ветствует формуле искусственного нейрона с линейной функцией активации [5].

Таким образом, модуль обратной вейвлет-де-композиции можно представить в виде нейронной сети с числом слоев, равных уровню разложения.

На рис. 2 представлено одноуровневое обратное преобразование Хаара [7] как слой нейронной сети. Здесь круги со знаком «+» означают функцию суммирования, со знаком «–» вычитания.

Детализирующие

Грубая версия

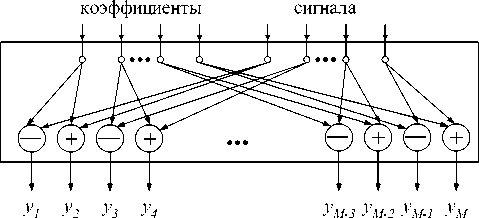
Рис. 2. Модуль одноуровневого обратного вейвлет-преобразования как слой нейронной сети

Таким образом, ИНС с модулем обратной вей-влет-декомпозиции может быть представлена как сложная нейронная сеть, в которой первые слои представляют собой некоторую стандартную нейронную сеть (например, многослойный перцептрон) и несколько слоев с линейными функциями активации, производящими обратное вейвлет-преобразование.

Пример такой нейронной сети, представляющей собой двухслойный перцептрон с модулем обратного преобразования Хаара, можно видеть на рис. 3.

Многослойный перцептрон

Модуль обратной вейвлет-декомпозиции

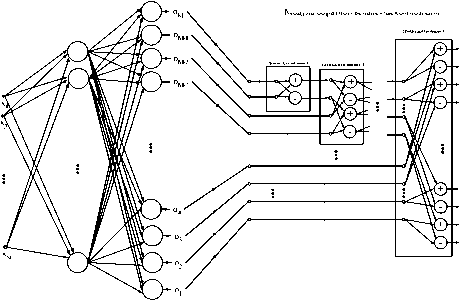
Рис. 3. ИНС из двухслойного перцептрона с модулем обратной вейвлет-декомпозиции Хаара

Использование для задач распознавания речи

Основная идея использования нейронных сетей с модулем обратной вейвлет-декомпозиции для задач распознавания речи заключается в сокращении области значений нейронной сети. В предыдущем разделе мы ввели целевую функцию как вероятность принадлежности данного участка распознаваемому звуку. Можно с уверенностью утверждать, что эта функция имеет большую степень гладкости, то есть что разность соседних отсчетов будет много меньше максимального значения, принимаемого активационной функцией выходного слоя:

|| p_2i - p_2i-1 ||<< M ,                    (2)

где M – амплитуда значений выходной активационной функции, а i = 1,2,3,… .

Практические эксперименты показывают, что || p_2i - p_2i-1 || гарантированно меньше M в 3-5 раз. Это позволяет найти такой коэффициент k , что k || p_2i - p_2i-1 || ≤ M . Применяя одноуровневое преобразование Хаара, мы получаем

^/■-^o^lK' + ^z-ill;

Таким образом, зная, что ~p2i -1 принимает ограниченные значения, мы можем без всякого риска умножить его на k. В виду ограниченности активационной функции эта операция сократит область поиска в k раз. Так, если мы используем биполярную активационную функцию с облас- тью значений (-1,1), а значения ~2i.—i е ^- 5;5j , то умножение на 5 позволит избежать поис-

ка нейронной сетью решений на отрезках

K ( j) =-------------7Г nH nH    nH (r = j-1

ZZ... Z   Пhir^2i i1 =1i2 =1 ij-2 =1 V r =1

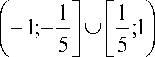
и сократить область значений

для j = N l ;

в 5 раз. В практических экспериментах был ис-

пользован размер выходного вектора равный 16. Возможность отмасштабировать каждый второй компонент вектора хотя бы в три раза уменьшает область значений (улучшает локализацию решения) в 6561 раз, в пять – в 390.625 раз! Таким об-

K i j ) =

ⁿ G n H     n H (        r = l -1

ZZ... Z  gii-2i-nhr^2i i1=1i2 =1  ij-2 =1 V          r=2

разом, мы получаем возможность учитывать априорную информацию о целевом векторе за счет линейного преобразования выходов, увеличивая стабильность и скорость работы нейронной сети за счет уменьшения зоны поиска и потери универсальности. При таком подходе нейронная сеть может аппроксимировать лишь узкий класс векторов, но, как показывают описанные ниже эксперименты, качество работы и скорость сходимости улучшается на порядки.

для j e [ 1; N l ) ; (8) q _j – выходное значение системы; w _i ^t _j – j -ый вес i - t ; x _i ^t – i -ое входное значение слоя t ; y _i ^t – i -ое выходное значение слоя t ; α – коэффициент скорости обучения.

Из этих формул мы видим, что в результате применения разложения целевой функции по временному базису происходит ранжирова-

Обучение нейронной сети с модулем обратной вейвлет-декомпозиции

Пусть модуль обратной вейвлет-декомпозиции осуществляет преобразование, обратное вейвлет-преобразованию, заданному двумя зеркальноквадратурными fIr фильтрами G и H, определяемыми коффициентами h_i и g_i .

Тогда для ИНС с модулем обратной декомпозиции имеют место формулы обучения, сходные с формулами метода обратного распространения ошибки:

ние выходов нейронной сети по значимости и каждый вход обучается со своей собственной скоростью, соответствующей его значимости в вычислении конечного результата, что способствует повышению устойчивости и скорости про-

цесса в целом.

^{( j)}

5INi , , ) = ( q i — P*^   , ------_? (4)

d i wNM xI к k=0           J

^δ i^t

n _t

t

= Z 51 ^

⎠

dy _i ^t

⎛ ⁿ t

,

^d ⎜^⎜ ∑ ^w k^ti ^x k^tj ⎟^⎟

V k = 0        7

J w t = -a • 3 j • x j .            (6)

Здесь o⁽ j ) - выходные значения ИНС (вейв-лет-коэффициенты), индекс j означает уровень

вейвлет-разложения, i уровне; формальная функция I(i, j) сопоставляет двумерному индексу (i,j) одномерный; коэффи-

Sq j циент к(j) = —J— do- j)

Результаты экспериментов

Тестирование и экспериментальная проверка нейронной сети с модулем обратной вейвлет-декомпозиции проводилась на задаче распознавания изолированного звука.

Для экспериментов был выбран речевой корпус из 37 слов. Проверка нейронной сети с модулем обратного вейвлет-разложения проводилась на задаче распознавания изолированного звука «а». Задача усложнялась тем, что длина звука в базе варьировалась в пределах четырехкратной от минимальной.

Целью эксперимента являлось сравнение двух абсолютно одинаковых нейронных сетей, с идентичной архитектурой, обучаемых одним и тем же алгоритмом, одна из которых обучалась с модулем вейвлет-разложения цели, а другая без него.

Оценка нейронных сетей проводилась следующим образом. Было проведено несколько запусков системы (здесь приводятся результаты для 20 запусков). В каждом запуске был выбран контрольный пример с худшим результатом и вычислено математическое ожидание ошибки по всем примерам контрольной выборки. По результатам двадцати запусков был выбран лучший результат по обоим критериям.

В ходе описанных экспериментов были получены следующие результаты (см. таблицу 1).

Таблица 1. Результаты экспериментов

Метод	Критерий №1,%	Критерий №2,%	Число эпох	Дисперсия
Перцептрон	11,57	17,83	3873	0,03028
Перцептрон с вейвлет-модулем	0,00330	0,00744	385	0,00016

Здесь «критерий №1» – это лучшее математическое ожидание ошибки на контрольной выборке по результатам обучения 20 нейронных сетей. Соответственно «критерий №2» – это лучшее математическое ожидание супремума ошибки на контрольной выборке по результатам обучения 20 нейронных сетей.

По результатам экспериментов можно говорить о примечательных результатах – которые, как это видно по дисперсии, весьма устойчивы. Можно также отметить резкое ускорение сходимости и качественное возрастание обобщающих способностей.

В таблице 2 приводятся дисперсия и математическое ожидание ошибки для эксперимента.

Таблица 2. Статистические характеристики

Метод	Математическое ожидание	Дисперсия
Перцептрон	15,50	0,03028
Перцептрон с вейвлет-модулем	0,014	0,00016

Из таблицы мы видим, что модуль вейв-лет-разложения позволяет получить результат с небольшим математическим ожиданием и смещением ошибки, что говорит о хорошем качестве решения и адаптивности метода [5].

Выводы