Использование вероятностно-статистических методов для анализа формирования генерационного потенциала глубокопогруженных отложений Верхнепечорской впадины

Верхнепечорская впадина в северной части Предуральского краевого прогиба приурочена к юго-восточной части Тимано-Печорской нефтегазоносной провинции. Месторождения углеводородов (УВ) в её пределах разрабатываются с 60-х гг. XX в., поэтому строение верхних горизонтов осадочного чехла изучено достаточно полно. При этом отложения, залегающие на глубине более 4 км и имеющие, как правило, возраст древнее поздневизейского, остаются неравно- мерно и слабо исследованными (Кузнецова, Галкин, 2023).

Структура характеризуется резко асимметричным строением, типичным для краевых прогибов. Наиболее прогнутая зона расположена у крутого восточного борта, где глубина залегания фундамента достигает 10 км и более. Западный борт впадины на всем протяжении отличается спокойным моноклинальным погружением слоев, изредка осложненным флексурами, террасами и структурными уступами, имеет строение близкое к платформенному типу.

В настоящее время в пределах Верхнепечорской впадины пробурено 46 глубоких скважин. Стоит отметить, что большинство из них приурочено к Вуктыльской тектонической пластине на востоке территории. Именно восточные районы характеризуются развитием глубокопогруженных отложений, изучение которых связано с рядом трудностей. Поэтому представляет интерес моделирование нефтегазоносности больших глубин с помощью различных методов (Кузнецова, Галкин, 2023).

В работе изучено формирование нефтегазогенерационного потенциала глубоких недр, а также факторы, влияющие на него. Общий генерационный потенциал – это количество УВ, которое порода может образовать в течение всего литогенеза или его конкретной стадии. Параметр определяется по результатам пиролитических исследований как сумма значений S 1 +S 2 (далее – S 1+2 ). Он зависит, прежде всего, от типа органического вещества (ОВ), его содержания – концентрации органического углерода ( Сорг ), а точнее, её исходных значений ( Сорг^и ).

Характеристика S 1+2 используется для расчета количества генерированных УВ, а с учетом миграционных потерь – для оценки прогнозных ресурсов. Сопоставление этих данных с геологическими запасами позволяет выявить скрытые резервы нефтегазоносного бассейна, в том числе в глубокопогру-женных отложениях старых районов добычи УВ, таких как юго-восточные районы Тима-но-Печорской нефтегазоносной провинции, где выделяется Верхнепечорская впадина.

Материалы и методы

Поскольку результаты пиролитических исследований часто отсутствуют или недоступны, должно быть полезно изучение связи S 1+2 с исходными значениями Сорг и тектоническими факторами.

Тектонические характеристики, такие как скорости погружения и седиментации, влияют на процессы нефте- и газообразования и, вероятно, на величину S 1+2 . Длительное и интенсивное погружение значительной территории это не только необходимое условие формирования осадочного бассейна, но и важный критерий зон максимальной концентрации УВ (Дьяконов и др., 2008; Кузнецова,

2019; Кузнецова, Галкин, 2023). Кроме того, влияние на формирование S 1+2 могут оказывать глубины залегания толщ и, конечно, мощности.

Скорости погружения глубокопогружен-ных толщ разреза Верхнепечорской впадины получены в результате 1D бассейнового моделирования с помощью программных комплексов Petromod и Genex скважин глубиной более 4 км. Методика бассейнового моделирования рассматривается во множестве работ (Галкин, Козлова, 2000; Галушкин, 2007; Allen, Allen, 2013; Al-Hajeri et al., 2009; Hantschel, Kauerauf, 2009; Schneider, 2003 и др.). Полученные значения учитывают уплотнение пород в течение геологического времени, использована процедура «разуплотнения».

Для определения перспектив использования значений концентраций Сорг и тектонических факторов для оценки генерационного потенциала отложений, в том числе глубо-копогруженных, выполнен вероятностностатистический анализ.

Для решения поставленной задачи использовались вероятностно-статистические методы, возможность использования которых при построении одномерных и многомерных линейных статистических моделей решалась путем использования элементов математической статистики и теории вероятностей. Использованные методы подробно рассмотрены в многочисленных отечественных и зарубежных трудах (Девис, 1990; Дрейпер, Смит, 2007; Кривощеков и др., 2010; Михалевич, 2006; Поротов, 2006; Путилов, 2014; Friedman, 1989; Montgomery, Peck, 1982; Yarus, 1983 и др.).

Результаты исследования

Для определения связи с S 1+2 важны исходные концентрации Сорг – Сорг^и . Эти значения, необходимые для дальнейшего анализа, получены по формулам, предложенным К.Е. Питерсом, С.С. Уолтерсом и Дж.М. Молдованом (Peters et al., 2007).

На первом этапе произведен расчет исходного водородного индекса по формуле:

Н1И=НИ-Ш^^3^, где HIи – исходный водородный индекс (до начала процесса генерации УВ), мг УВ/г Сорг; HI – водородный индекс (по данным пиролиза), мг УВ/г Сорг; Tmax – температура максимального выхода УВ при крекинге керогена, °С.

Затем рассчитана степень реализации нефтегазоматеринской породой исходного генерационного потенциала – коэффициент трансформации:

Ши-Н1 1200

HIH 1200HI

X1OO%.

где TR (transformation ratio) – коэффициент трансформации, %; HI^и – исходный водородный индекс (до начала генерации УВ), мг УВ/г Сорг; HI – водородный индекс (по данным пиролиза), мг УВ/г Сорг; 1200 – коэффициент, учитывающий количество УВ, образующихся на единицу массы органического углерода, мг УВ/г Сорг.

Наконец, на основе полученных HI^и и TR определено исходное содержание органического углерода Сорг^и :

Сорги= СсрхН1ихСорг

H Iй x (1 -TR) x (Ccp -Copr)+ (HIxCopr)J где Сорги – исходное содержание органического углерода (до начала генерации УВ), %; Сорг – содержание органического углерода

(по данным пиролиза), %; HI^и – исходный водородный индекс (до начала генерации УВ), мг УВ/г Сорг; HI – водородный индекс (по данным пиролиза), мг УВ/г Сорг; TR – коэффициент трансформации, доли единицы; С ср – среднее содержание углерода в сгенерированных УВ – 83,33 %.

В случае отсутствия результатов пиролиза или части из них (например, T max ), необходимых для определения Сорг^и , в расчетах использовались современные значения Сорг .

Для сравнения средних значений генерационного потенциала S 1+2 (мг УВ/г Сорг), Сорг^и (%), скоростей погружения Vп (м/млн. л), глубины отбора проб Нп (м) и мощностей слоев h (м) ОВ глубокопогру-женных отложений Верхнепечорской впадины было разделено на две группы, отвечающие тектоническому районированию территории: ОВ западной зоны (внешний борт) и ОВ восточной зоны (внутренний борт). А затем на три подгруппы: сапропелевое, смешанное и гумусовое ОВ. Для анализа, прежде всего, были использованы описательная статистика и t -тест.

Средние значения перечисленных показателей по тектоническим зонами и типам ОВ приведены в табл. 1 и 2.

Таблица 1. Сравнение средних значений показателей по западной зоне

Показатели, ед. изм.	C Средние значения \min-max/			Критерии t p
	Тип ОВ, количество наблюдений
	Сапропелевое, 21	Смешанное, 16	Гумусовое, 31
1	2	3	4	5
S 1+2 , мг УВ/г Сорг	0,344±0,283 0,047–1,235	0,977±1,18 0,046–4,89		-2,38171 0,022802
	0,344±0,283 0,047–1,235		0,362±0,458 0,042–1,982	-0,15967 0,873786
		0,977±1,18 0,046–4,89	0,362±0,458 0,042–1,982	2,572576 0,013464
Сорги, %	0,299±0,322 0,01–1,23	0,611±0,677 0,05–2,29		-1,85825 0,071561
	0,299±0,322 0,01–1,23		0,771±1,71 0,007–6,45	-1,2472 0,218134
		0,611±0,677 0,05–2,29	0,771±1,71 0,007–6,45	-0,35933 0,721026

Окончание табл. 1

1	2	3	4	5
Vп, м/млн. л	51,24±21,02 12,0–72,0	61,81±49,91 15,0–170,0		-0,87709 0,386417
	51,24±21,02 12,0–72,0		74,87±65,24 15,0–175,0	-1,60026 0,115842
		61,81±49,91 15,0–170,0	74,87±65,24 15,0–175,0	-0,70045 0,487249
Нп, м	4803,52±393,14 4385,5–5564,5	3783,81±719,04 3047,0–5213,0		5,519982 0,000003
	4803,52±393,14 4385,5–5564,5		3960,55±702,29 2946,5–5258,5	4,986702 0,000008
		3783,81±719,04 3047,0–5213,0	3960,55±702,29 2946,5–5258,5	-0,811025 0,421620
h, м	324,33±163,15 81,0–576,0	408,46±326,06 90,0–946,0		-1,02634 0,311775
	324,33±163,15 81,0–576,0		317,81±258,31 90,0–946,0	0,102582 0,918705
		408,46±326,06 90,0–946,0	317,81±258,31 90,0–946,0	1,042213 0,30288

Таблица 2. Сравнение средних значений показателей по восточной зоне

Показатели, ед. изм.	Средние значения \ min—max/			Критерии t p
	Тип ОВ, количество наблюдений
	Сапропелевое, 6	Смешанное, 24	Гумусовое, 62
1	2	3	4	5
S 1+2 , мг УВ/г Сорг	0,498±0,615 0,16–1,74	0,332±0,267 0,06–1,23		1,024369 0,31443
	0,498±0,615 0,16–1,74		0,284±0,195 0,013–1,171	1,989328 0,050812
		0,332±0,267 0,06–1,23	0,284±0,195 0,013–1,171	0,932422 0,353791
Сорги, %	0,088±0,094 0,011–0,266	0,407±0,434 0,031–1,755		-1,76570 0,08835
	0,088±0,094 0,011–0,266		1,332±1,37 0–6,47	-2,208667 0,030675
		0,407±0,434 0,031–1,755	1,332±1,37 0–6,47	-3,23695 0,00173
Vп, м/млн. л	60,00±5,48 55,–65,0	43,67±31,99 19,0–161,0		1,230159 0,228873
	60,00±5,48 55,–65,0		55,50±21,81 32,0–161,0	0,500705 0,618245

Окончание табл. 2

1	2	3	4	5
		43,67±31,99 19,0–161,0	55,50±21,81 32,0–161,0	-1,96782 0,052389
Нп, м	6409,58±364,50 6071,5–6987,5	5397,40±356,83 4726,5–6040,0		6,190670 0,000001
	6409,58±364,50 6071,5–6987,5		4958,27±326,77 4487,0–5800,0	10,293289 0,000000
		5397,40±356,83 4726,5–6040,0	4958,27±326,77 4487,0–5800,0	5,448164 0,0000005
h, м	474,5±178,0 312,0–637,0	255,79±135,62 124,0–693,0		3,325087 0,002476
	474,5±178,0 312,0–637,0		470,08±148,85 178,0–693,0	0,037411 0,97027
		255,79±135,62 124,0–693,0	470,08±148,85 178,0–693,0	-6,189759 0,000000

Анализ данных позволил определить, что:

• -    статистические различия в средних значениях по S 1+2 наблюдаются в западной тектонической зоне как между смешанным и гумусовым, так и между смешанным и сапропелевым ОВ;

• -    по показателю Cорг^и статистические различия в средних значениях обнаружены в восточной зоне между сапропелевым и смешанным, равно как и между смешанным и гумусовым ОВ;

• -    по показателю Vп средние значения статистически не различаются;

• -    по Нп статистическое различие в средних значениях получено в обеих зонах, на западе – между сапропелевым и смешанным, а также сапропелевым и гумусовым ОВ, на востоке – между всем типами ОВ;

• -    по h статистические различия в средних значениях выявлены в восточной зоне между сапропелевым и смешанным, смешанным и гумусовым ОВ.

Для понимания процесса формирования значений S 1+2 в зависимости от Сорг , Нп , Vп и h были построены поля корреляции между изучаемыми показателями в пределах западной и восточной зон Верхнепечорской впадины. Анализ этих полей корреляции выявил, что соотношения и сила корреляционных связей в пределах рассматриваемых типов ОВ и тектонических зон значительно отличаются.

Для количественной оценки корреляционных связей вычислены значения коэффи- циентов корреляции – r, не только между S1+2 и выбранными показателями, но и между значениями самих показателей. Это позволило на количественном уровне оценить влияние каждого из них на величину S1+2 и определить, как статистически связаны между собой показатели, которые формируют значения S1+2. Значения коэффициентов r приведены в табл. 3.

Анализ значений коэффициентов корреляции показал, что между S 1+2 и выделенными показателями, а также между последними наблюдаются как положительные, так и отрицательные связи с различной степенью тесноты.

Для сапропелевого ОВ в пределах западной тектонической зоны на S 1+2 максимальное влияние оказывает Сорг^и , в меньшей степени – h (слабая обратная связь). На востоке наблюдается максимальное влияние Нп (сильная положительная связь) и слабое – h (также положительная связь), Vп и Сорг^и (отрицательная связь). В целом в пределах Верхнепечорской впадины наблюдаются статистически значимые связи с Сорг^и и Нп .

На S 1+2 смешанного ОВ западной зоны влияют значения Сорг^и (сильная прямая связь) и Vп (слабая обратная зависимость). Восточнее наблюдается прямая зависимость, умеренная – от Сорг^и , слабая – от Vп и h .

Таблица 3. Корреляционная матрица

	Западная зона					Восточная зона
	S 1+2	Сорги	Нп 1	Vп 1	h	S 1+2	Сорги	Нп 1	Vп 1	h
Сапропелевое ОВ
S 1+2	1					1
Сорги	0,38 *	1				-0,16	1
Нп	-0,02	-0,40	1			0,73	-0,36	1
Vп	-0,01	0,48	-0,94	1		-0,38	0,49	0,86	1
h	-0,21	0,21	-0,25	0,37	1	0,38	-0,49	0,86	-1,00	1
Смешанное ОВ
S 1+2	1					1
Сорги	0,76	1				0,59	1
Нп	-0,07	-0,38	1			-0,04	-0,02	1
Vп	-0,13	-0,30	0,63	1		0,20	0,06	-0,39	1
h	-0,09	-0,20	0,29	0,91	1	0,25	0,11	-0,24	0,90	1
Гумусовое ОВ
S 1+2	1					1
Сорги	0,73	1				0,11	1
Нп	-0,44	-0,43	1			-0,21	-0,21	1
Vп	-0,35	-0,33	0,76	1		-0,02	-0,04	0,07	1
h	-0,17	-0,24	0,73	0,51	1	0,16	0,08	-0,03	0,53	1

* Подчеркнуты статистически значимые корреляционные связи

В пределах рассматриваемой территории в целом наблюдается заметная прямая зависимость от Сорг и слабая обратная – от Нп .

На западе территории на S 1+2 гумусового ОВ сильно и прямо влияет Сорг^и , умеренная обратная зависимость наблюдается от Нп и Vп , слабая – от h . На востоке на данный параметр оказывает влияние Нп (отрицательная связь), в меньшей степени – Сорг^и и h (положительная связь). В целом наблюдается заметная прямая зависимость от Сорг^и и слабая обратная от Нп и Vп , h находится на рубеже статистической значимости.

Значения коэффициентов r отличаются в зависимости от типа ОВ и тектонического строения, но и взаимоотношения изучаемых показателей также значительно разнятся.

Детальный анализ построенных корреляционных полей показал, что для всех типов ОВ в пределах полей наблюдаются подполя. Поэтому для комплексной оценки различий в средних значениях изучаемых показателей и соотношений между ними использован линейный дискриминантный анализ.

Прежде всего, рассмотрены три группы ОВ без разделения на тектонические зоны. В результате реализации указанного метода построены следующие линейные дискрими- нантные функции:

Z 1 = 1, 423S 1+2 – 0,62 Сорг + 0,0007 Нп – 0,0036 Vп – 0,002 h – 2,407, при R = 0,504, χ ² = 51,444, р = 0,0000001;

Z 2 = -1,094 S 1+2 – 0,042 Сорг + 0,0008 Нп – 0,0039 Vп + 0,001h – 3,692, при R = 0,195, χ ² = 5,994, р = 0,1996.

Линейная дискриминантная функция Z 1 является статистически значимой, Z 2 – нет.

По данным функциям были вычислены значения Z 1 и Z 2 , их соотношение в зависимости от типов ОВ приведено на рис. 1, из которого видно, что по значениям Z 1 и Z 2 изучаемая выборка в определенной мере (64,4 %) делится на типы ОВ.

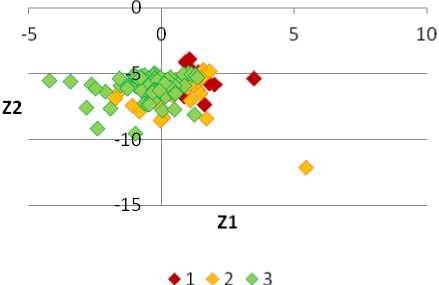
Рис. 1. Соотношение между Z 1 и Z 2 для выделенных классов ОВ. Условные обозначения: 1 – са-прпелевое ОВ; 2 – смешанное ОВ; 3 – гумусовое ОВ

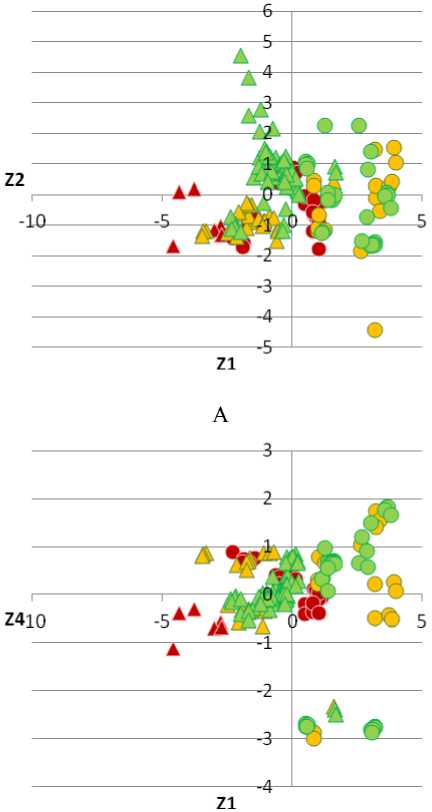
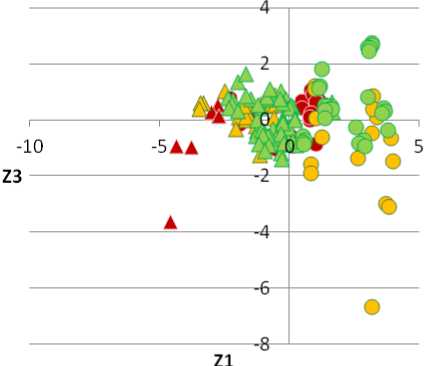
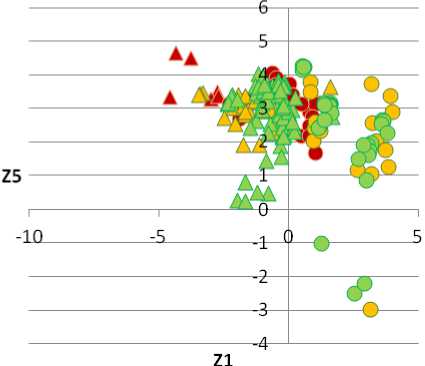
Аналогично выполнен линейный дискриминантный анализ для выделенных типов ОВ с разделением на тектонические зоны, т.е. для 6 групп. В результате построено 5 линейных дискриминантных функций, обобщенных в табл. 4 .

Линейные дискриминантные функции Z 1 , Z 2 , Z 3 являются статистически значимыми, Z 4 и Z 5 – нет. По данным функциям были вычислены значения Z 1 , Z 2 , Z 3 , Z 4 и Z 5 .

Таблица 4. Параметры линейных дискриминантных функций

	Свободный член	Коэффициенты при:					R	χ 2	p
		S 1+2	Cорги	Нп	Vп	h
Z 1	10,115	0,314	-0,229	-0,0023	0,0149	-0,0003	0,84	282,29	0,0000
Z 2	0,557	-1,084	0,601	-0,0004	-0,0076	0,004	0,53	86,79	0,0000
Z 3	1,311	-1,708	0,301	-0,00003	0,0129	-0,0038	0,42	35,55	0,0000
Z 4	3,333	-0,389	-0,089	-0,00038	-0,0259	0,0005	0,16	5,82	0,2133
Z 5	1,517	-0,883	-0,601	-0,00029	-0,0064	0,0028	0,10	1,67	0,1968

В

Б

Г

Рис. 2. Соотношение между значениями Z для выделенных типов ОВ и зон их распространения: А – Z 1 и Z 2 ; Б – Z 1 и Z 3 ; В – Z 1 и Z 4 ; Г – Z 1 и Z 5 . Условные обозначения: 1 – сапропелевое ОВ западной зоны; 2 – сапропелевое ОВ восточной зоны; 3 – смешанное ОВ западной зоны; 4 – смешанное ОВ восточной зоны; 5 – гумусовое ОВ западной зоны; 6 – гумусовое ОВ восточной зоны

Наличие сложных по виду корреляционных полей влияния значений характеристик Сорг^и, Нп, Vп и h на S 1+ 2 для изучаемых типов ОВ указывает на то, что необходимо более детально изучить эти соотношения с помощью пошагового регрессионного анализа. Для учета многообразия различных, в ряде случаев разнонаправленных, влияний выделенных показателей на величину S 1+2 для сапропелевого ОВ построены 18 многомерных моделей для западного борта впадины и 3 – для восточного. Кроме того, рассчитаны уравнения для смешанного ОВ (12 – для западной зоны и 18 – для восточной), а также гумусового типа (21 и 58 уравнений, соответственно).

На основе моделей формирования значений S1+2 от Сорги, Нп, Vп и h для разных типов ОВ, полученных по результатам пошаго- вого регрессионного анализа, построены графики, приведенные на рис. 3–7.

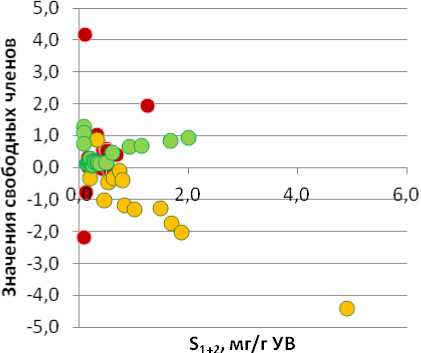
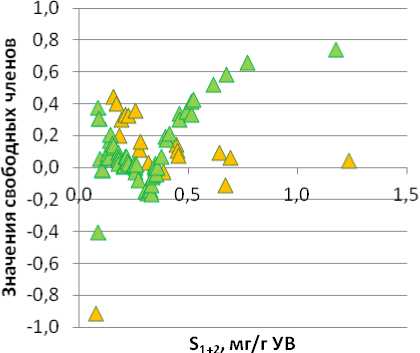
Из графика изменения свободных членов уравнений регрессии, построенных для западной тектонической зоны (рис. 3А), видно, что они значительно отличаются для выделенных типов ОВ. Анализ поведения данных зависимостей продемонстрировал, что для сапропелевого и гумусового ОВ значения свободных членов уравнений регрессии выполняют корректировку величин Сорг^и со знаком «плюс», тогда как смешанного ОВ со знаком «минус». График, построенный для восточной зоны (рис. 3Б), подтверждает сделанные ранее выводы. Но стоит отметить, что для данной территории характерны меньшие значения свободных членов уравнений.

А

Б

Рис. 3. Изменение свободных членов уравнений регрессии в зависимости от S 1+2 для разных типов

ОВ: А – западная зона; Б – восточная зона. Усл. обозн. см. на рис. 2

А

Б

Рис. 4. Изменение коэффициентов при Сорг^и в зависимости от S 1+2 для разных типов ОВ: А – западная зона; Б – восточная зона. Усл. обозн. см. на рис. 2

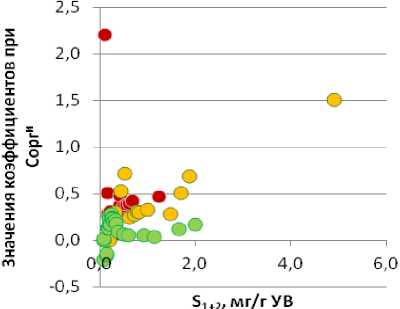
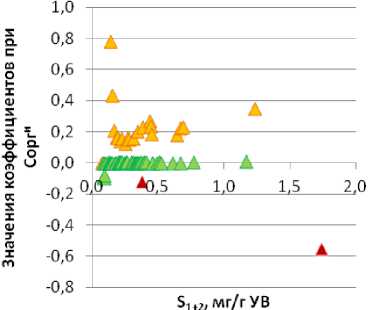
Из графика изменения коэффициентов при Сорг^и (рис. 4А) в уравнениях регрессии, построенных для западной зоны, видно, что они значительно отличаются для сапропелевого и гумусового ОВ. Для смешанного ОВ величины коэффициентов располагаются между ними, примыкая к значениям, рассчитанным для сапропелевого ОВ. Анализ поведения данных зависимостей показал, что для всех типов ОВ значения коэффициентов при Сорг^и уравнений регрессии в разной степени выполняют корректировку значений S 1+2 со знаком «плюс». График изменения коэффициентов при Сорг^и (рис. 4Б) в уравнениях регрессии восточных районов выявил, что для них характерны меньшие значения данного параметра. Анализ поведения рассматриваемых зависимостей показал, что для сапропелевого ОВ значения коэффициентов при Сорг уравнений регрессии выполняют корректировку значений S 1+2 со знаком «минус», для смешанного ОВ – со знаком «плюс», а для гумусового ОВ их величины весьма невысоки и близки к 0.

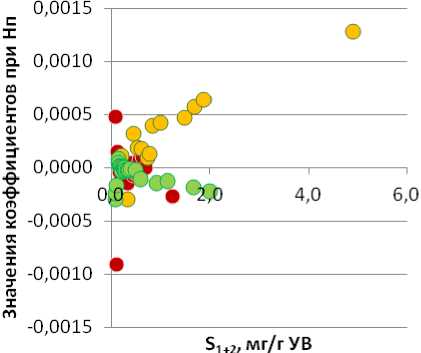
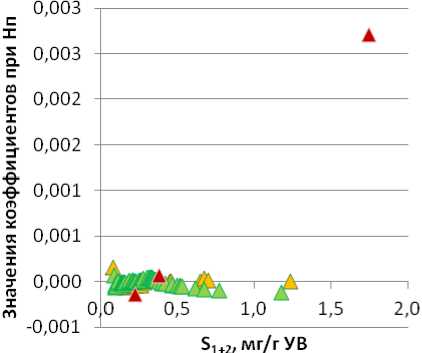
График изменения коэффициентов при Нп (рис. 5А) в уравнениях регрессии, рассчитанных для западной тектонической зоны, отличается от описанных ранее тем, что прямая связь рассматриваемых значений

S 1+2 обнаружена для смешанного ОВ, а для сапропелевого и гумусового ОВ – обратная. При этом последние значения достаточно близки. Для сапропелевого и гумусового ОВ значения коэффициентов при Нп уравнений регрессии выполняют корректировку значений S 1+2 со знаком «минус», тогда как смешанного ОВ – со знаком «плюс». Аналогичный график (рис. 5Б), построенный для восточных районов, продемонстрировал, что величины коэффициентов при Нп уравнений регрессии значительно отличаются для сапропелевого и гумусового ОВ. Для смешанного ОВ значения коэффициентов располагаются между ними, примыкая к величинам, рассчитанным для гумусового ОВ, при этом последние значения достаточно близки и невелики. Анализ поведения данных зависимостей позволил определить, что для сапропелевого ОВ значения коэффициентов при Нп уравнений регрессии выполняют корректировку значений S 1+2 со знаком «плюс», тогда как смешанного и гумусового ОВ – со знаком «минус».

Все это в очередной раз подтверждает, что формирование модельных значений происходит в принципиально различных условиях в зависимости от типа ОВ и тектонического районирования.

А                                Б

Рис. 5. Изменение коэффициентов при Hп в зависимости от S 1+2 для разных типов ОВ: А – западная зона; Б – восточная зона. Усл. обозн. см. на рис. 2

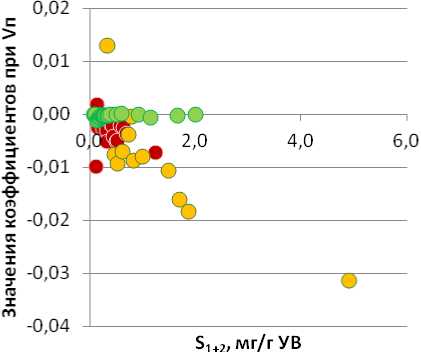
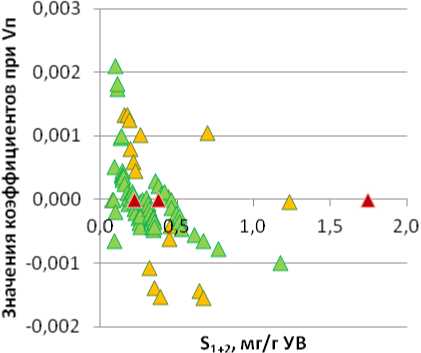
При этом последние близки к 0. Для сапропелевого и смешанного ОВ величины рассматриваемого коэффициента уравнений регрессии выполняют корректировку значений S 1+2 со знаком «минус», тогда как для гумусового ОВ – со знаком «плюс», но весьма незначительно.

Рассчитанный для восточной тектонической зоны график изменения коэффициентов при Vп (рис. 6Б) в уравнениях регрессии показал, что эта характеристика значительно отличается для сапропелевого и гумусового ОВ. Для смешанного ОВ величины коэффициентов при Vп близки к значениям, рассчитанным для гумусового ОВ. Для сапропелевого ОВ значения рассматриваемых коэффициентов уравнений регрессии выполняют корректировку значений S 1+2 со знаком «плюс», но влияние весьма невелико, значения близки к 0, тогда как для смешанного и гумусового ОВ – со знаком «минус».

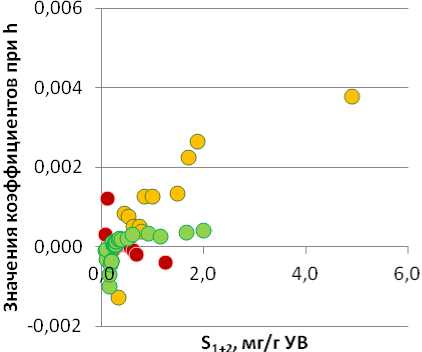
График изменения коэффициентов при h (рис. 7А) в уравнениях регрессии, рассчитанных для западной зоны, показал, что они значительно отличаются для сапропелевого и гумусового ОВ. Для смешанного ОВ величины коэффициентов близки к значениям, рассчитанным для гумусового ОВ. Для сапропелевого ОВ значения коэффициентов при h в уравнении регрессии выполняют корректировку значений S 1+2 со знаком «минус», значения близки к 0, тогда как для смешанного и гумусового ОВ – со знаком «плюс».

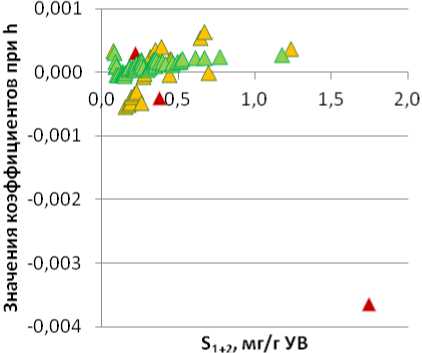
График изменения коэффициентов при h (рис. 7Б) в уравнениях регрессии, рассчитанных для восточной зоны, имеет схожую организацию, но отличается меньшим диапазоном значений и близостью величин параметров уравнений регрессии, рассчитанных для смешанного и гумусового ОВ.

Изменение значений коэффициентов множественной корреляции уравнений регрессии, рассчитанных для западной тектонической зоны, позволило определить, что при увеличении значений S 1+2 диапазон изменения R для сапропелевого ОВ незначителен, а для смешанного и гумусового ОВ – весьма существенен. В пределах восточной зоны определена та же закономерность.

Из графика изменения коэффициентов R и значений уровней достигаемой статистической значимости р для разных типов ОВ видно, что значения достаточно хаотичны, но для гумусового ОВ западной тектонической зоны наблюдается определенный тренд изменения.

Проведенный пошаговый регрессионный анализ позволил выявить различное изменение ряда параметров уравнений регрессии для различных типов ОВ в пределах западной и восточной зон, позволил определить, что формирование модельных значений S 1+2 ^М происходит в принципиально различных условиях в зависимости от типа ОВ и тектонического положения.

А

Б

Рис. 6. Изменение коэффициентов при Vп в зависимости от S 1+2 для разных типов ОВ: А – западная зона; Б – восточная зона. Усл. обозн. см. на рис. 2

А                              Б

Рис. 7. Изменение коэффициентов при h в зависимости от S 1+2 для разных типов ОВ: А – западная зона; Б – восточная зона. Усл. обозн. см. на рис. 2

Обсуждение и заключение

Выполненный вероятностно-статистический анализ формирования нефтегазогенерационного потенциала для различных типов ОВ показал, что он в первую очередь определяется исходными концентрациями Сорг , а также тектоническими условиями – скоростью погружения, глубиной залегания (отбора проб) и мощностью отложений. Ранее (Кузнецова, Галкин, 2023) было доказано влияние первых двух факторов на формирование значений Сорг для выделенных типов ОВ. При этом стоит отметить, что характер изменения рассматриваемых свойств для S 1+2 и Сорг различается.

Кроме того, дискриминантный анализ продемонстрировал, что рассматриваемая выборка более чем на 60 % разделяется как на три группы по типам ОВ, так и на 6 групп с учетом состава ОВ и тектонического районирования.

Также с помощью пошагового регрессионного анализа доказано, что формирование модельных значений S 1+2 происходит в принципиально различных условиях в зависимости от типа ОВ и тектонического положения.

Проведенные исследования показали, что не только Сорг, но и тектонические характеристики могут использоваться при картировании и оценке свойств нефтегазоматеринских пород изучаемых глубокозалегающих отложений территории Верхнепечорской впадины, а также определении объемов генерированных УВ.