Использование волноводного резонанса для создания нанооптических спектральных пропускающих фильтров

Совершенствование технологий изготовления наноструктур открывает новые возможности при создании современных оптических устройств. Наноимпринтинг (nanoimprinting lithography или hot embossing lithography) является перспективным методом недорогого массового производства наноструктур [1]. Этот метод позволяет изготавливать одномерные и двумерные многослойные структуры.

Спектральные фильтры как отражающие, так и пропускающие, применяются во многих оптических устройствах. Традиционным способом изготовления таких фильтров является нанесение десятков, а иногда и сотен тонкопленочных слоев различных материалов. Путем интерференционного сложения и вычитания интенсивности света при переотражении на границах слоев достигаются требуемы е характеристики спектрального фильтра. Использование волноводного резонанса позволяет на порядки уменьшить количество наносимых слоев и таким образом удешевить процесс изготовления фильтра и уменьшить его толщину.

След ует отметить несколько опубликованных работ, посвященных расчету спектральных фильтров. Например, в работе [2] получен пропускающий спектральный фильтр с эффективностью 40%. Статья [3] описывает расчет отражающего спектрального фильтра. В работе [4] описаны пропускающие спектральные фильтры с эффективностью 60-80%. В статье [5] для создания пропускающего фильтра использована металлическая дифракционная решетка. Однако полученные в вышеперечисленных работах наноструктуры не предназначены для их последующего изготовления методом наноимпринтинга. Кроме того, в указанных работах нет описания метода, который использовался для оптимизации структуры спектрального фильтра.

Далее будут рассмотрены структуры, обеспечивающие возникновение волноводного резонанса, используемые методы расчета электромагнитного поля в таких структурах, а также параллельные асинхронные стохастические методы оптимизаци и подобных структур на вычислительном кластере.

Постановка задачи

В данной работе рассмотрена оптимизация нано-фотонных структур на примере многослойного пропускающего спектрального фильтра. Принцип работы этого оптического устройства базируется на волноводном резонансе (guided-mode resonance – GMR) [6]. В отличие от плазмонного резонанса для возбуждения GMR не требуется использование металла.

На рис. 1 а представлен пример простой структуры, в которой возможно возникновение волноводного резонанса. Пусть диэлектрическая проницаемость волновода описывается след ующей ф унк цией

е( x ) = E g

, f 2nx ) + Де cos --- ,

l Л J

где Л - период модуляции диэлектрической проницаемости волновода.

Согласно теории связанных волн, распространение света в таком однослойном волноводе описывается след ующим уравнением

d ² E i ( z )

dz ²

к 2 E g

- k ²1 .JE sin 0-

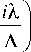
x E i ( z ) + 2 k ^{2 д}е [ E i - i ( z ) + E i + i ( z ) ] = 0

X

,        (2)

где % - длина волны падающего света, E i - амплитуда плоской волны, соответствующей i -му порядку, z – координата, перпендикулярная направлению волновода, к - волновое число, 0 - угол падения света. В случае отсутствия модуляции диэлектрической проницаемости волновода ( Де =0 ) приведенное уравнение переходит в волновое уравнение для диэлектрического волновода.

На рис. 1 а схематически показаны также пути нулевых прошедшего и отраженного дифракционных порядков.

На рис. 1 б показана еще одна простая схема однослойного волноводного резонатора, в котором дифракционная решетка служит одновременно и волноводом, и средством ввода падающего света в этот волновод. В общем случае две эти функ ции могут

выполняться двумя различными слоями структуры. Рассмотрим случай нормального падения света на структуру, при котором для отражения и пропускания используются только нулевые дифракционные порядки. Тогда для возникновения волноводного резонанса должно выполняться следующее условие:

% f

<л<% ,

где е f - усредненная диэлектрическая проницаемость, рассчитанная в соответствии с теорией эффективной среды. Выражение (3) позволяет приблизительно оценить значение периода дифрационной решетки.

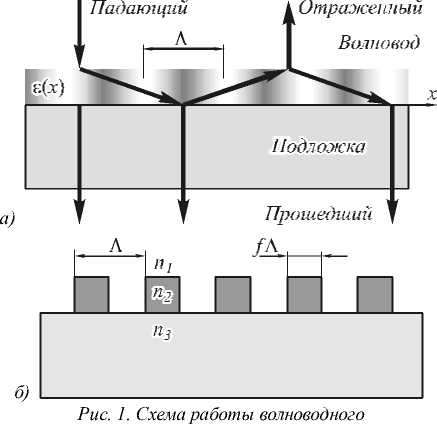
спектрального фильтра

Согласно теории эффективной среды можно аппроксимировать усредненную диэлектрическую проницаемость волновода на рис. 1 б следующими функциями:

е f = ( 1 - f ) n + fn 2 (4)

для TE- поляризации , и

TM е f

( n 1 n 2 ) 2

( 1 ^- f ) n 22 ^{+ f}n 1²

для TM-поляризации. Здесь f – коэффициент заполненности периода решетки.

Для точного анализа наноструктур, которые обеспечивают возникновение волноводного резонанса, т реб ует ся использовать векторные методы расчета дифракции электромагнитного поля. Для этого в данной работе использован RCWA (Rigorous Сoupled-Wave Analysis) алгоритм [7-11], основанный на методе Фурье-мод.

Оптимизация структуры спектрального фильтра

Геометрические параметры волновода и решетки, а также свойства материалов используются для оптимизации рассчитываемого спектрального фильтра. Создаваемый спектральный фильтр может быть отражающим или пропускающим, а также одно- или многополосным. Рассмотрим процесс проектирования однополосного пропускающего спектрального фильтра. За основу оптимизируемого фильтра взята структура, изображенная на рис. 2. Несколько параметров этой структуры зафиксированы. Прежде всего, это характеристики матери алов. Чтобы расширить список пригодных для использования материалов, величина n2 выбрана относительно малой (n2 =2). Оставшиеся материалы – это воздух (n1 = 1) и стандартный пластик (n3 = 1,5). Коэффициент заполненности периода решетки f полагается равным 1/2.

Толщина 1-го и 3-го слоев считается одинаковой ( d ), т.к. полагается, что для изготовления будет использован метод наноимпринтинга. Таким образом, оптимизируются пять оставшихся параметров: Л , d, t, w, v .

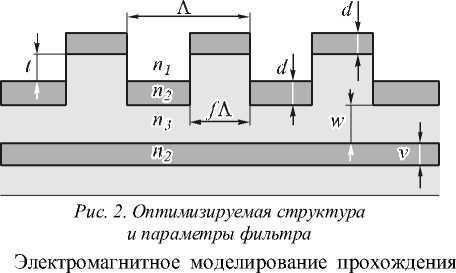
света через многослойную структуру, включающую элементы рельефа с размером порядка длины волны падающего света, является ресурсоемкой задачей [12]. Тем более ресурсоемкой является оптимизация подобных наноструктур. Учитывая, что методом оптимизации, как правило, является стохастический метод поиска глобального экстремума, решение данной задачи с помощью высокопроизводительных вычислительных средств – суперкомпьютера или кластера – становится оправданным [13, 14].

В качестве метода оптимизации выбрана асинхронная параллельная реализация метода PSO (Particle Swarm Optimization) [15, 16]. На рис. 3 показан псевдокод асинхронного последовательного алгоритма PSO. Семантика данного алгоритма базируется на аналогии с пчелиным роем, который занят поисками наиболее медоносной области.

• •    Инициализация начальных данных

• ■    Задать входные параметры

• ■    Случайным образом инициализировать точки решений и их скорости

• Оптимизация

• •    Цикл по количеству итераций, индекс к

• ♦    Цикл по количеству точек решений, индекс i

• ♦    Рассчитать функцию критерия Кх) )

• •    Проверить условие схождения алгоритма

• •    Обновить значения точек решений и их скоростей

• •    Вывод результатов

Рис. 3. Псевдокод асинхронного последовательного алгоритма PSO

В качестве функц ии критерия выбрано отклонение рассчитанного значения прошедшего 0-го дифракционного порядка от заданного для требуемого спектрального диапазона f ПТ? T^esiedd W" T   W] I ,       (6)

к M x                    у где М – количество отсчетов спектрального диапазона, по которым выполняется оптимизация.

Рис. 4 демонстрирует отличие асинхронного параллельного метода PSO от его синхронного аналога. Асинхронность алгоритма важна для эффективного использования ресурсов кластера или суперкомпьютера, в частности, в гетерогенной среде.

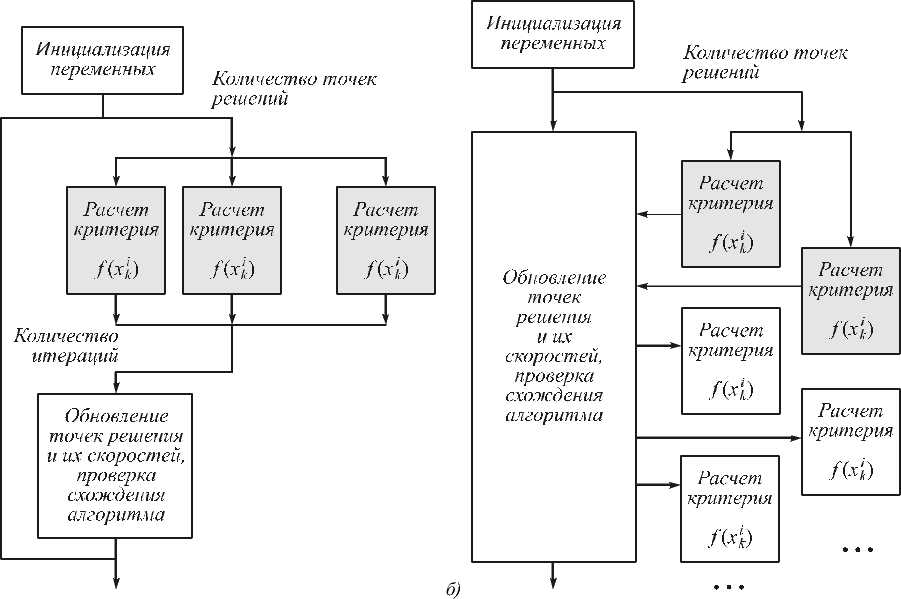
Рис. 4. Блок-схемы параллельного синхронного алгоритма PSO (а) и параллельного асинхронного алгоритма PSO (б)

Качество рассчитанного спектрального фильтра будем оценивать по след ующим параметрам: эффективность и контраст. Эффективностью фильтра E будем считать количество энергии, пропущенное фильтром в 0-м порядке на центральной длине волны расчетного спектрального диапазона. Контраст фильтра б удем рассчитывать по формуле

K =

E max

^^^^^^e

E .

min

E + E .

max min

где E max – значение максимума спектрального фильтра, а E min – максимальное значение по другую сторону от E max по отношению к одному из двух локальных минимумов (рис. 5).

Спектральный фильтр в данной работе рассчитывался для ТЕ-поляризованного падающего света. Количество точек решений при оптимизации данной структуры выбрано равным 20. Функция критерия строилась по 9 отсчетам в спектральном диапазоне от 540 нм до 560 нм с шагом 2,5 нм. В результате оптимизации получены следующие значения параметров (нм): Л =431,92, d = 356, t = 340,56, w =436,48, v =313,8. Для получения решения выполнено ~200 тыс. расчетов функции крит ерия.

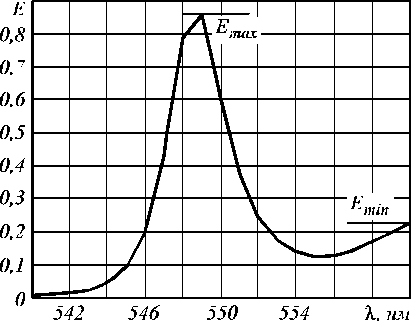
Рис. 5. Расчет контраста фильтра

Расчет допусков погрешностей изготовления и использования спектрального фильтра

Экспериментальный образец, или оттиск, для наноимпринтинга создается напылением материала с высоким индексом рефракции на дифракционную решетку, изготовленную из материала с низким индексом рефракции. Первоначальная дифракционная решетка может быть изготовлена, например, с по-

мощью относительно недорогого метода интерферометрической литографии (interferometric lithography) [17].

При изготовлении наноструктуры, рассчитанной в предыдущем пункте, мог ут возникнуть по-грешно сти, характерны е для метода наноимпринтинга. Например, глубина оттиска может отличаться от расчетной. В этом случ ае толщина слоя t (рис. 2) нано структуры находится в некото ром диапазоне [ t_min, t_max ].

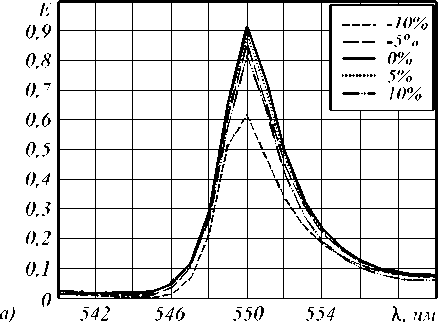
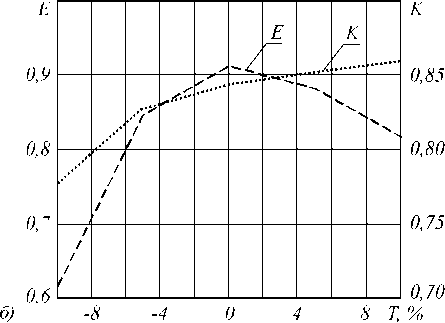
Рис. 6. Спектральные кривые (а) и контраст (б) для погрешности глубины оттиска при наноимпринтинге

На рис. 6 а показано , что при отклонении в ели-чины t от расчетной в диапазоне от -10% до +10% (т.е. погрешность T лежит в этом диапазоне) форма спектральной кривой фильтра меняется слабо. Эф-фектив ность фильтра меня ется менее, чем на 10%, если t лежит в диапазоне от -5% до +10%. Контраст фильтра (рис. 6 б ) также остается достаточно стабильным.

В качестве еще одного примера погрешности изготовления рассмотрим отклонение коэффициента заполненности периода решетки от требуемого значения 1/2. Несколько спектральных кривых, соответствующих такой погрешности, приведены на рис. 7а. Допуски в диапазоне от -10% до +10% для эффективности и контраста фильтра показаны на рис. 7б. Для данного типа погрешности пик спектральной кривой существенно смещается от заданного значе- ния. При этом эффективность и контраст фильтра уменьшаются слабо.

В завершение оценим требования к точности юстировки при использовании рассчитанного фильтра. Спектральные кривые для случая, когда угол падения света на фильтр отличается от нормального, приведены на рис. 8 а . Очевидно, что данный фильтр чувствителен к погрешности угла падения света. Для отклонения угла падения более чем на ±2 градуса эффективность фильтра существенно снижается. Контраст фильтра также значительно падает (рис. 8 б ).

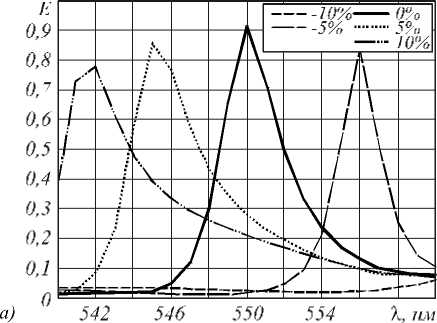
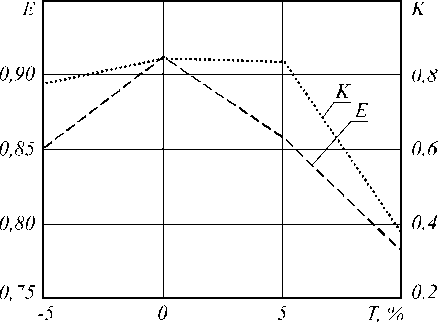
Рис. 7. Спектральные кривые (а) и контраст (б) для погрешности коэффициента заполненности дифракционной решетки при наноимпринтинге

Отметим, что информация о требуемых допусках изготовления наноструктуры может быть включена в критерий качества оптимизационного алгоритма. В этом случае возможен более гибкий дизайн фильтра с учетом, например, особенностей технологической уст ановки для изготовления фильтра или условий использования фильтра.

Заключение

Описанные в настоящ ей ст атье структуры и полученные результаты позволяют сд елать след ую -щие выводы. Во-первых, фильтры с волноводным резонансом используют на порядки меньш ее количество тонкопленочных слоев , чем традиционные фильтры. Во-вторых, показана возмо жность создания высокоэффективных (более 90%) пропускаю- щих спектральных фильтров, при изготовлении которых используются материалы с достаточно низким коэффициентом рефракции. Это расширяет список материалов для производств а подобных фильтров. В-треть их, продемонстрирована возможность про ектирования таких фильтров для изготовления методом наноимпринтинга. Применение в д анной работе параллельных стохастических методов оптимизаци и с асинхронным б алансом загрузки суперкомпьютера позволяет повысить качество нанооптических устройств при неизменном времени, затрачиваемом на расчет подобных устройств . Таким образом, можно говорить об относительно недорогом массовом производстве нанооп-тических пропускающих спектральных фильтров , использующих волноводный резонанс.

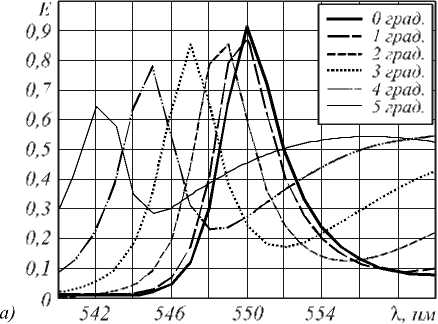
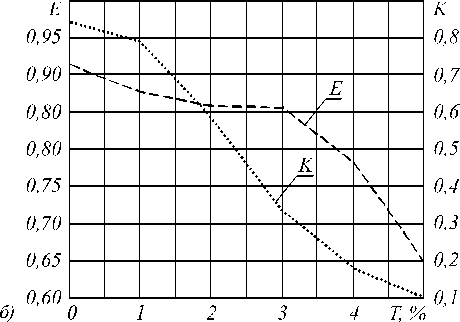
Рис. 8. Спектральные кривые (а) и контраст (б) для отклонения угла падения от нормального при использовании изготовленного фильтра

Работа выполнена при поддержке гранта Президента РФ для ведущих научных школ № НШ-7414.2010.9 и грантов Российского фонда фундаментальных исследований №№ 09-07-12147-офи_м, 09-07-92421-КЭ_а, 10-07-00553-а.