Использование волнового уравнения при исследовании физических процессов

Волновое уравнение - линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.

d²f d²? d²5  1 d²?

dx2 dy2 dz2   u2 dt2

Удовлетворяющее однородным граничным условиям

^(0, t) = ^( l, t) = о, и начальным условиям

^ ( x ,0) = ^ ( x ),

§'t( x,0) = V( x )•

r

A 0 - произвольная комплексная константа интегрирования.

Монохроматическая волна — это волна, в каждой пространственной точке которой колебания происходят только на одной частоте ω.

Рассмотрим, как выглядит частное решение для различных величин:

r(t, r ) = AoCOs((k, r ) - ®t) _      уравнение      плоской      волны, распространяющейся вдоль оси Х. Здесь ξ(x,t) – смещение точек среды с координатой x в момент времени t; A – амплитуда волны; ω –циклическая частота; k - волновой вектор.

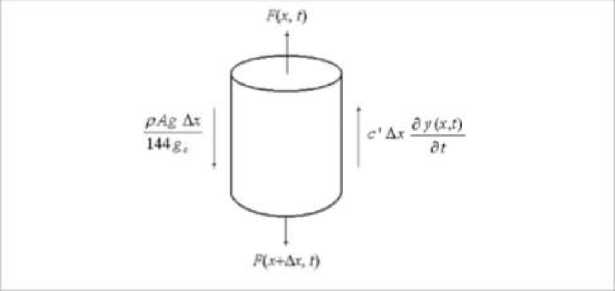
Задача: «Шар радиуса R= 50 см находится в немагнитной и непроводящей среде. В среде распространяется плоская электромагнитная волна, длина которой λ<

Для начала запишем волновое уравнение для нашей струны.

15Тхх д t1      дx x

Решение будет иметь структуру:

§ = X (x) • T (t)

Взяв частные производные от выражения выше, мы получим систему:

' T "tt

--------=

T

X xx

—

I X

-to2

-to2

где ω – циклическая частота.

Решая её, мы получим:

T(t) = A cos tot + B sin tot,

^X(x) = С^cos ^ ^{x +}D^sin ^ ^x, где k = — - волновой вектор.

Преобразуя по формуле Эйлера:

T(t) = M • e-^{ito t} , здесь знак условен (в другом разделе физики ставят знак «+»), X(x) = L • eikx⁽, где M и L - произвольные постоянные.

Так как ^(x, t) = X(x) • T(t) , то ^(x, t) = M • L • e ltot+ikx. Так как M и L - произвольные постоянные, то их можно заменить одной постоянной.

^(x, t) = Ae"i(kx-to) = A (cos(kx - tot) +1 • sin(kx - tot))

Но физический смысл имеет только действительная часть, поэтому будем учитывать только первое слагаемое:

5(x, t) = A cos(kx - tot).

Для нашей задачи:

—►

E = E_ocos(rot — kx)

Из курса распространения электромагнитных волн вектор Пойтинга определяется как

S = [E x H ],

E - напряжённость электрического поля, a H

- напряжённость магнитного поля, которая меняется по закону:

H = H0 cos(rot — kx), а [e x H ]= Е • Н • sin(E H).

Мы знаем, что в электромагнитном поле вектора

—           —

^k,

——

——

правую тройку, следовательно, угол между E и H равен угла равен 1.

E и H образуют 90, а значит синус

Далее нам известно свойство электромагниной волны

V^E=4°^H •

Отсюда

H =

V eoeE 00

По условию о=1 и e =1. Затем мы умножим числитель и знаменатель на Йе

H = ^ео E

V °0^е0

С =

, где              - скорость света в вакууме.

N °0е0

h = Ee c.

Подставим предыдущее выражение в формулу для вектора пойтинга: S = E2еc = (E_o cos(rot — kx))2 е₀c.

Но нам требуется найти среднее значение по времени, поэтому

^\

= E² cos²(ωt -kx) ε c = E²ε c = 0                0       00

S = (E cos(ωt - kx))²ε c = E²

= ¹⋅(200)²3⋅10⁸⋅8,85⋅10^-12=53,1Вт/м².

В оптике из волнового уравнения выводятся различные физические величины, которые характеризуют оптическую среду. Например, зная плотность потока энергии, то есть вектор Пойтинга, можно определить интенсивность падающего света. Далее можно определить показатель преломления среды с помощь формулы, выразив из неё n:

I=

cn_{⋅ E0}2 8πµ

, где μ – магнитная проницаемость среды, а n – показатель

преломления.

В рефрактометрии используется метод исследования веществ, основанный на определении показателя (коэффициента) преломления (рефракции) и некоторых его функций.

Например, эксперементально измеряя интенсивность излучения гелионеонового лазера, луч которого проходит через стекло до попадания на датчик, можно определить показатель преломения вещетсва, пропуская через него волны определённой длины.

I, Вт/м2 142 160 0,26 77 0,1 E, В/м 47,67 25,29 1,019 17,55 0,632 N 1,52 1,09 2,096 2,091 2,096 nср=1,776, nстекла=1,5.

Неожиданным применением волнового уравнения стало его использование в нефтяной промышленности, описание которого было рассмотрено Сэмом

Гэвином Гиббсом2. Здесь им воспользовались для вычисления устойчивости упругого весомого стержня переменной изгибной жесткости. Это известное уравнение возникает из ньютоновской динамики и закона упругости Гука. Поскольку трение в скважине в системе накачки штока не может быть проигнорировано, решение будет включать это трение.

На рисунке показаны силы, действующие на элемент стержня длиной Δх с изменением глубины х.

Запишем волновое уравнение в общем виде с учётом силы трения:

d²y ( x, t) d t¹

= и и

d²y ( x, t) dx x

dy (x, t) ∂t

^{+ g} (*),

Где c- коэффициент сопротивления движению жидкости.

Силы F (x, t) и F (x + x, t) являются осевыми силами вдоль стержня. Закон Ньютона утверждает, что нескомпенсированные силы, действующие на элемент стрежня, вызывают его ускорение. Использование этого закона требует, чтобы скорости и ускорения относились к фиксированной системе координат, скажем, относительно обсадной колонны скважины.

pA Ax d²y (x, t)                            dy (x, t)  pAg Ax

= F(x + Ax,t)-F(x,t)-c^Ax        +       .

144gc   dt²                                   St     144 gc

Используя определение частной производной и переходя к пределу при x → 0, получим pA  д2 y (x, t) = dF (x, t) _ , dy (x, t)   pAg

144g_c   дt²        дx          dt     144g_c'

Используя закон Гука, дy (x, t )

F⁽x, t) = EA ———, где e - модуль Юнга,

Мы получим уравнение (*), в котором

144 c'g_c ρA

144 Egc υ=       ^c и

ρ

Две основные проблемы при использовании стрежня: диагностирование проблем в действующей установке и проектирование новых установок. Обе эти задачи могут быть выполнены путем решения волновых уравнений. Решения волнового уравнения, которые удовлетворяют измеренным временным характеристикам стержневой нагрузки F (0, t) и положения u (0, t) на поверхности, позволяют определить для временных диаграмм нагрузки на скважинный насос F (L, t) и положения y (L, t).

2 20000

К

Из этих решений могут быть выведены условия работы скважинного насоса, а также можно исправить проблемы с эксплуатацией и выполнить любые другие действия по оптимизации.

С его помощью можно узнать, как распространяется возмущение от верхнего конца к нижнему и соответствует ли это эталонному распространению. Если при сопоставлении графиков волновых процессов наблюдаются значительные отклонения, можно предсказать, какие происходят деформации. Также с высокой долей вероятности можно предсказать дальнейшее поведение стрежня (например, его поломку).

Таким образом, волновое уравнение можно использовать для описания различных физических процессов, предсказывать, к чему они могут привести. Важно, что при построении модели и сопоставлении с реальной системой, можно заметить отклонения или искажения, которые в дальнейшем повлекут за собой серьёзные последствия.