Использование возможностей динамической среды GeoGebra в условиях дистанционного обучения математике

Одним из приоритетных направлений развития образования в России является внедрение моделей непрерывного образования, способных обеспечить реализацию индивидуального маршрута обучения. Рассматривая образовательный процесс с такой позиции, его неотъемлемой частью становится дистанционное обучение.

Проблемой дистанционного обучения занимались многие исследователи, например, Л.П. Давыдов, О.Б. Журавлева, Э.Г. Скибицкий, рассматривали его как новую ступень заочного образования [10]. Согласно определению Е.С. Полат дистанционное обучение представляет собой форму организации образовательного процесса, в основе которой лежит осуществление обучения на расстоянии с применением интерактивных технологий и сохранением компонентов, присущих учебному процессу [6]. Такая форма организации образовательного процесса способствует активизации познавательной деятельности обучающихся, направлена на развитие их творческих способностей и позволяет обеспечить разнообразие образовательных услуг и гибкость организационной структуры для каждого независимо от многих составляющих, таких как географическое положение, состояние здоровья и др.

При организации дистанционного обучения содержание образования остается прежним, однако меняются подходы к его структурированию, поэтому используемые средства обучения должны быть интегрированы в информационно-образовательную среду. Для эффективности дистанционного обучения математике необходимо разработать в достаточном объеме методические материалы, способствующие прочному закреплению знаний и демонстрации положительных сторон рассматриваемой технологии обучения.

Перечисленные требования выражаются в обеспечении дидактического принципа наглядности в обучении и воспитания у школьников навыков самостоятельной работы, поэтому к основным задачам учителя можно отнести следующие: проектирование индивидуального образовательного маршрута обучающегося, управление его самостоятельной работой по освоению содержания учебного ма- териала, выбор оптимальных платформ для представления теоретического и задачного материала, а также оценивания качества знаний, внедрение в образовательный процесс цифровых образовательных технологий и интерактивных методов [9, 11]. Комплексное сочетание нескольких программных компонентов, таких как Moodle, GeoGebra, Wingeom, MathCad, MicrosoftTeams и др. создает возможность разработки обучающих сред, способных удовлетворить возрастающие потребности общества, связанные с содержанием обучения математике [6].

В процессе исследования был проведен опрос [5] среди обучающихся, их родителей и педагогов по математике – представителей разных образовательных учреждений г. Оренбурга, затрагивающий проблему дистанционного обучения математике. Респондентам были заданы следующие вопросы:

• 1.    Имело ли место в Вашем обучении / в обучении Вашего ребенка / в Вашей профессиональной деятельности дистанционное обучение математике с применением ЦОР?

• 2.    Как Вы относитесь к дистанционному обучению математике?

• 3.    Какая форма изучения математики, по Вашему мнению, является наиболее удобной?

• 4.    С какими цифровыми образовательными ресурсами в обучении математике Вы знакомы?

Результаты опроса приведены в табл. Показатели вычислялись отдельно для каждой категории – обучающийся, родитель, педагог по математике.

Таблица

Результаты опроса

Форма обучения	Обучающиеся, %	Родители обучающихся, %	Педагоги-математики, %
Традиционная	51	71	43
Дистанционная (с применением ЦОР)	49	29	57

По мнению опрошенных обучающихся и их родителей основная проблема заключается в сложности самостоятельной организации своей деятельности и труднодоступности материала. Кроме того, результаты опроса показали, что большинство родителей обучающихся не знакомы с цифровыми образовательными технологиями в обучении математике. Это, во многом, могло повлиять на негативное отношение к технологии дистанционного обучения с их стороны. В то же время было установлено, что 49% обучающихся положительно относятся к дистанционному формату обучения с применением ЦОР. Такой показатель связан с доступностью дистанционного формата обучения и возможностью обучения по индивидуальному маршруту. Такого же мнения придерживаются 57% учителей математики.

Результаты опроса подтверждают гипотезу о необходимости конструирования как можно большего числа методических разработок, применимых для осуществления дистанционного обучения математике. Остановимся подробно на модели математического занятия по теме «Квадратичная функция». Предложенные материалы могут быть рекомендованы учителям математики с целью внедрения интерактивных технологий в образовательный процесс при изучении математики. Структура занятия является универсальной и может быть использована как при дистанционном формате обучения, так и притрадиционном. Перечисленные положения характеризуют практическую значимость результатов исследования.

Тема «Квадратичная функция» является фундаментом школьного математического образования, при ее изучении закладываются основы аналитического мышления, формируется соответствующая интуиция, развивается логическое мышление и математическая культура обучающихся [1, 7]. Занятие имеет исследовательский характер и проводится в форме лабораторной работы по математике в среде GeoGebra.

GeoGebra – это динамическая математическая программа, которая включает в себя геометрию, алгебру, таблицы, графы, статистику и арифметику [14]. При разработке дистанционных учебных курсов основной упор делается на индивидуальную работу обучающихся. Предложенную лабораторную работу, напротив, можно сделать парной или групповой. Данная среда является свободно распространяемой и доступна для использования, как учителем, так и обучающимися при различных формах проведения занятий и при различной компьютерной оснащенности учебного класса.

Использование интерактивной динамической среды, а именно ресурса GeoGebra, на данном уроке оказывает эффективное влияние на развитие познавательного интереса обучающихся за счет интерактивности средств, лёгкости построения чертежей, высокой степени наглядности и доступности; оптимизацию образовательного процесса за счёт рационального использования времени на различных этапах урока; снижение эмоционального напряжения на уроке [3, 4]. Особое внимание следует уделить важности доказательств основных положений, когда первые интуитивные представления обучающегося бывают неверны или справедливы только для частных случаев. Такие условия следует выяснить аналитически, проиллюстрировав их затем с помощью динамической среды GeoGebra.

В основе лабораторной работы лежит исследование свойств функции y = ax² + bx + cy = ax² + bx + c , зависимости ее поведения от коэффициентов a, b, c и преобразования графика квадратичной функции. Такой подход позволяет не только демонстрировать обучающимся графики квадратичной функции, но и рассматривать преобразования, не затрачивая при этом лишнее время на построения.

Лабораторная работа включает в себя 4 задания разной степени сложности [8, 13]. Для выполнения заданий обучающимся предложены интерактивные чертежи, позволяющий менять значение коэффициента a, b, c (рис. 1) и выполнять преобразования графика квадратичной функции (см. рис. 2 на с. 39).

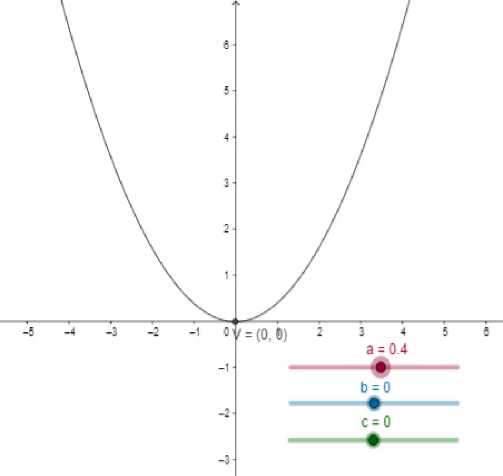
Рис. 1. Модель заданий № 1–3

Задание № 1. Уравнение квадратичной функции y = ax² + bx + cy = ax² + bx + c представляет собой параболу ( a≠0)a≠0 ) . Апплет содержит 3 ползунка: ползунок «а», ползунок «b», ползунок «c». Меняя положение ползунков ответьте на вопросы:

• 1.    Какое влияние оказывает параметр а на график функции?

• 2.    Какое влияние оказывает параметр b на график функции?

• 3.    Какое влияние оказывает параметр c на график функции?

Задание № 2. При а= 0 а= 0 парабола вырождается в прямую. Объясните, почему произошло такое преобразование графика функции.

Задание № 3. Меняя положение ползунков, проанализируйте, какие изменения происходят в уравнении функции и ее графика (функциональная зависимость меняется при изменении положения любого ползунка).

Ответьте на вопросы:

• 1.    Как параметр b виден в уравнении параболы?

• 2.    Как параметр c виден в уравнении параболы?

• 3.    Являются ли координаты (x, y) вершины параболы очевидными в ее уравнении? Если да, то как?

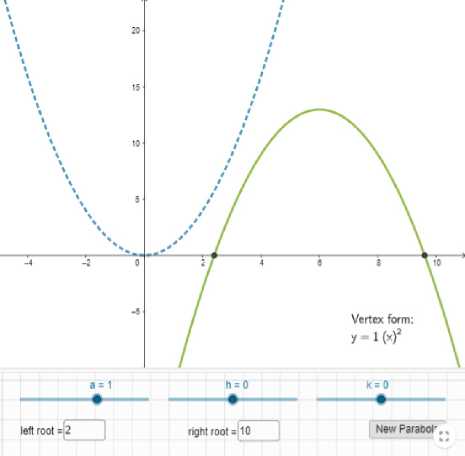
Рис. 2. Модель задания № 4

Задание № 4. Используйте ползунки, чтобы преобразовать синий график в зеленый. Если парабола пересекает ось x, найдите корни (с точностью до 2 знаков после запятой).

Для оценивания качества знаний обучающихся контроль предложен в форме тестирования с помощью сервиса Google Формы. Критерии перевода баллов в отметки предложены в описании к тестированию. Тестирование включает в себя 9 заданий, характер заданий может быть различным. Например, установление соответствия между графиком квадратичной функции и формулой, которая его задает, графическое решение систем уравнений, определение наибольшего и наименьшего значения функции и др. Подробно рассмотрим пример одного из заданий (см. рис. 3 на с. 40). Другие задания тестирования доступны по ссылке [12].

Задание № 5. Используя график функции (см. риc. 3 на с. 40), заполните пропуски в формуле y = (x+к )² + hy = (x+к)² + h, которая его задает. В ответе укажите соответствующие коэффициенты k и h в указанном порядке без пробелов.

Сервис Google Формы является мобильным и доступным, позволяет собирать данные и автоматически обрабатывать результат. Кроме того, предоставлена возможность формирования отчета по выполнению заданий в виде таблицы и составления рейтинга в группе обучающихся, выполнивших задание. Тестирование представляет включает в себя как задания закрытого типа, так и открытого, и может быть рекомендовано обучающимся, успешно справившимся с заданиями лабораторной работы. Задание № 5 требует краткого ответа и оценивается в 2 балла.

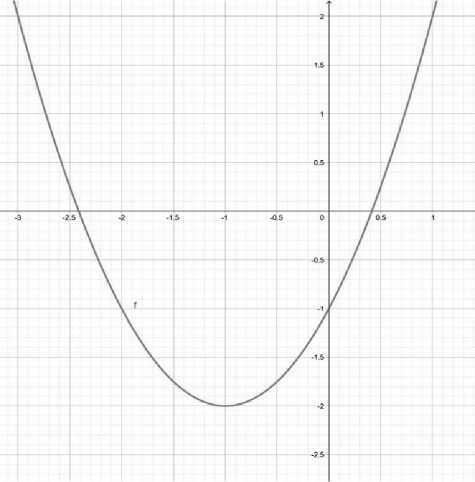
Рис. 3. Модель задания № 5

Дистанционное обучение математике, как востребованная образовательная технология, позволяет сделать обучение качественным и доступным. Прослеживая развитие и совершенствование системы дистанционного обучения, как одного из приоритетных направлений развития открытого образовательного пространства, можно отметить его распространение за последние несколько лет. Информационно-образовательная среда во многом определяет специфику взаимодействия между всеми субъектами обучения.

Ориентация системы дистанционного обучения на индивидуальность каждого его участника повышает значимость диагностической функции на всех этапах обучения по сравнению с традиционной формой обучения. Использование возможностей инновационных средств обучения в образовательном процессе, в частности динамической среды GeoGebra, активизирует познавательную деятельность обучающихся, оптимизирует образовательный процесс и позволяет осуществлять дифференцированный подход в обучении, тем самым повышая качество математической подготовки обучающихся.