Использование закона распределения хи-квадрат для аналитического описания статистик биометрических параметров

В статье рассматривается проблема аппроксимации распределений параметров реальных биометрических образов из тестовых баз. Показано, что минимальную ошибку дает нормированное хи-квадрат распределение, которое может использоваться при сертификации систем аутентификации по тайным рукописным паролям.

Механизмы дистанционной высоконадежной биометрической аутентификации пользователей могут использоваться для защиты различных систем от несанкционированного доступа, либо проверки авторства при электронном документообороте. Созданные макеты (биометрико-нейросетевые контейнеры) по заверениям производителей обладают стойкостью к атакам подбора равной 10-12. Данные характеристики должны быть подтверждены статистическим тестированием на реальных данных. Очевидно, что сбор баз реальных биометрических примеров, необходимых для тестирования высоконадёжных систем, потребует огромного времени и затрат [1]. Высокая надежность – это высокий размер тестовых баз. Таким образом, появляется потребность в механизмах, позволяющих оценивать стойкость высоконадежных биометрико-нейросетевых систем на сокращенных выборках. Так, зная закон распределения значений биометрических данных, можно существенно сократить число тестовых примеров для получения «качественной» оценки. Для этого надо осуществить классификацию параметров и добиться нужной представительности тестовой выборки в каждом из подклассов.

При формировании больших баз тестовых образов можно классифицировать вводимые образы по группам стабильности, уникальности и качества их параметров [2]. Таким образом, для каждого образа из базы тестовых образов должны быть указаны средняя стабильность, средняя уникальность и среднее качество всех биометрических параметров данного образа. Далее встаёт проблема выбора закона, позволяющего описывать распределение параметров стабильности, уникальности и качества с максимальной достоверностью.

Описание преобразователей биометрии пользователя в код доступа строится с использованием классических законов распределения значений. Например, для оценки стойкости средства аутентификации к атакам подбора используется биномиальный закон, а для проверки гипотезы закона совместного распределения биометрических параметров – хи-квадрат распределение. Классические варианты этих законов построены на предположении независимости входных параметров [3]. Получаемые с их помощью оценки оказываются завышенными для случая реальных (зависимых между собой) биометрических данных. Для получения более достоверных статистических оценок необходимо при описании распределений биометрических параметров использовать классические законы распределений, имеющие аналитическое описание.

При аппроксимации симметричных эмпирических распределений выборок хорошо под- ходит нормальный закон распределения для подавляющего большинства биометрических приложений. Однако в биометрических приложениях с асимметричными распределениями использовать нормальный закон нельзя из-за появления значительных погрешностей. Вместо нормального закона распределения в статье предлагается использовать нормированное хи-квадрат распределение. Зная математическое ожидание распределения экспериментально полученных данных и число степеней свободы, построение численного или аналитического хи-квадрат распределения не вызывает особых затруднений.

Возможность использования нормированного распределения хи-квадрат для описания распределения функционалов биометрических образов проиллюстрируем для тестовых баз рукописных образов. Для этого возьмем обучающие выборки 100 пользователей «Свой», в каждой выборке содержится 20 примеров рукописного слова длиной 5 букв, и 2000 образов «Чужой» по одному примеру рукописного слова длиной 5 букв. Вычислим положение и степень разбросанности биометрических параметров всех используемых распределений. Полученные значения математических ожиданий и дисперсии используем для расчёта стабильности, уникальности и качества параметров тестовых образов.

При вычислении показателя стабильности i -го контролируемого биометрического параметра необходимо воспользоваться формулой:

^ Чужой ⁽ v i ) _х ^, (1)

^ Свой ( v , )

где <7 Чужой ( v i ) - стандартное отклонение i -го биометрического параметра множества образов «Чужой»; <7 Свой ( v i ) - стандартное отклонение i -го биометрического параметра множества образов «Свой».

Чтобы распределить биометрические образы по классам средней стабильности воспроизведения их параметров, необходимо учитывать показатель средней стабильности всех параметров классифицируемого биометрического образа. Средняя стабильность E ( c ( v )) рассчитывается как среднее арифметическое всех контролируемых параметров c ( v ) биометрического образа. Гистограмма плотности распределения средней стабильности биометрических параметров тестовых образов и найденная плотность нормированного хи-квадрат распределения представлены на рис. 1.

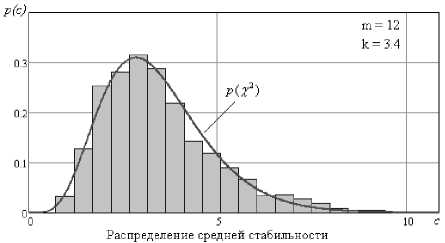
Рис. 1. Распределение средней стабильности биометрических параметров тестовых образов

Визуально видно, что полученное распределение имеет положительную асимметрию, что подтверждает невозможность использования нормального закона распределения значений для описания данного распределения. Распределения средней стабильности имеет следующие характеристики: математическое ожидание – 3,452; стандартное отклонение – 1,517; коэффициент асимметрии – 1,045.

Данные характеристики использовали при нахождении параметров нормированного хи-квадрат распределения. Для нахождения оптимальной функции аппроксимации использовался метод наименьших квадратов. Подбиралось количество степеней свободы и корректирующий коэффициент (смещение математического ожидания) таким образом, чтобы основные статистические моменты двух распределений стали максимально близки, то есть ошибка расхождения двух плотностей распределения стала минимальной.

В итоге оптимальной найденной функцией является нормированное распределений хи-квадрат с числом степеней свободы равным 12 и корректирующим коэффициентом равным 3,4: математическое ожидание – 3,401; стандартное отклонение – 1,389; коэффициент асимметрии – 0,82; ошибка расхождения – 0,091.

Следующим этапом стало нахождение закона, описывающего распределение средней уникальности параметров тестовых образов. Показатель уникальности i -го биометрического параметра, отражающий отличие контролируемого параметра от среднестатистического значения этого параметра, характерного для всех пользователей, вычисляется по формуле:

u ( v i ) =

\E„ . (v ) — E, . (v.

Чужой i Свой i

^ Чужой ⁽ v i )

где E    ( v, ) - математическое ожидание i -го

Чужой i биометрического параметра множества биомет- рических образов «Чужой»; ЕСвой (vi) — математическое ожидание i-го биометрического параметра множества биометрических образов «Свой».

Показатель средней уникальности всех параметров биометрического образа, вычисляется по формуле:

E (u(^v i )) = -^ u ⁽ v_i ).           (3)

ⁿ i =1

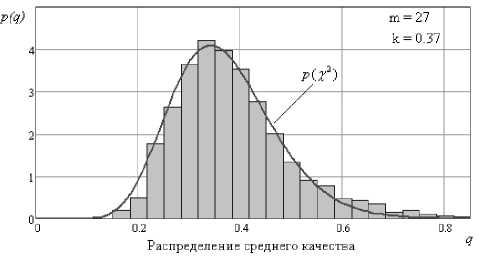
Рис. 3. Распределение среднего качества параметров биометрических образов

Полученная гистограмма плотности распределения средней уникальности и найденная плотность нормированного хи-квадрат распределения представлены на рис. 2.

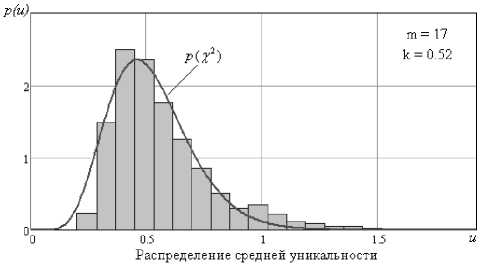
Рис. 2. Распределение средней уникальности параметров биометрических образов

Основные моменты экспериментально полученного распределения следующие: математическое ожидание – 0,568; стандартное отклонение – 0,223; коэффициент асимметрии – 1,551.

Оптимальной функцией, описывающей распределение средней уникальности функционалов тестовых образов, является нормированное хи-квадрат распределение с 17 степенями свободы и корректирующим коэффициентом равным 0,52: математическое ожидание – 0,52; стандартное отклонение – 0,179; коэффициент асимметрии – 0,69; ошибка расхождения – 0,157. Зная основные статистические моменты распределения параметров множеств «Свой» и «Чужой» можно вычислить среднее качество. Показатель качества i-го биометрического параметра, вычисляется как q (vi) =

\е„ .(v)-E_r - (v )| Чужой i Свой i •

CFrr (V.) + CT/-, ^(v )

Чужой i Свой i

На рис. 3 представлены гистограмма плотности распределения среднего качества и описывающая данное распределение плотность нормированного распределения хи-квадрат.

Для распределения среднего качества функционалов тестовых образов получили следую-щиемоменты:математическоеожидание–0,385; стандартное отклонение – 0,11 1; коэффициент асимметрии – 0,95.

Минимальное расхождение плотностей распределения получается при аппроксимации функцией нормированного хи-квадрат с 27 степенями свободы и корректирующим коэффициентом равным 0,37: математическое ожидание – 0,37; стандартное отклонение – 0,101; коэффициент асимметрии – 0,544; ошибка расхождения – 0,096.

Приведенные исследования параметров реальных тестовых образов, показали, что нормированное распределение хи-квадрат достаточно качественно описывает распределения средней стабильности, уникальности и качества параметров биометрических образов. Площади плотностей распределения для средней стабильности расходятся на 9,1%, для средней уникальности – на 15,7% и для среднего качества – на 9,6%.

Снизить ошибку расхождения можно только перейдя от целого значения количества степеней свободы к дробному (фрактальному). На рис. 4 представлен график зависимости ошибки расхождения (площадь расхождения исходного распределения и распределения описывающей функции) от числа степеней свободы. Точки А (11,75; 0,089), В (17,2; 0,156) и С (26,9; 0,096) на рис. 4 показывают оптимальное количество степеней свободы, при котором ошибка минимальна. В нашем примере минимальную ошибку при описании распределения средней стабильности дает нормированное хи-квадрат распределение с 11,75 степенями свободы. Для описания распределения средней уникальности необходимо использовать хи-квадрат с 17,2 степенями, а качества – 26,9.

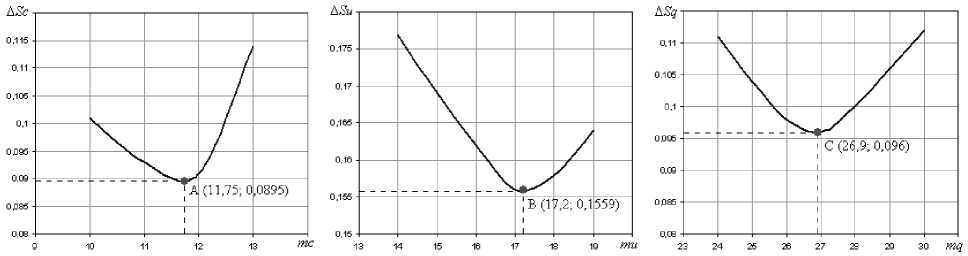
Рис. 4. Графики зависимости ошибки расхождения распределения от числа степеней свободы

Необходимо отметить, что фракталы (дробные показатели степени) принципиальны для низких степеней свободы, так как эти распределения отличаются значительно. При высоких степенях свободы можно брать целые значения степени (см. рис. 5).

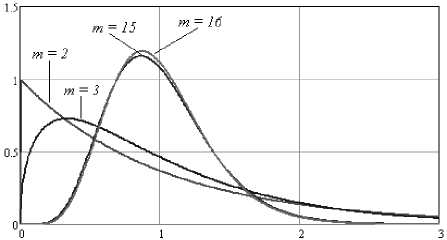
Рис. 5. Плотности распределения для m = 2; 3; 15 и 16

На рис. 5 представлены плотности нормированного хи-квадрат распределения для различного числа степеней свободы. Так плотность распределения для двух степеней свободы и плотность распределения для трех степеней расходятся более чем на 21%. В то же время расхождение плотностей распределения для 15 и 16 степеней свободы расходятся всего на 3%. Таким образом, видно, что переход к фракталам для относительно большого числа степеней свободы нецелесообразен.

Проведенные эксперименты для набора тестовых биометрических образов показали, что при описании распределений биометрических параметров можно использовать нормированное хи-квадрат распределение с целым либо дробным числом степеней свобода. Знание закона распределения позволяет правильно «размножать» обучающие либо тестовые образы при тестировании высоконадёжных средств биометрической аутентификации. Отвечает на вопросы как и сколько размножать. То есть. технология увеличения размеров тестовых баз и сколько нужно примеров, чтобы равномерно заполнить пространство всех биометрических параметров.

Можно выделить следующие направления, в которых предлагается использовать полученные знания о законе распределения биометрических параметров.

• 1.    Использование для классификации пользователей по группам стойкости, уникальности и качества. Это можно проводить при формировании тестовых баз биометрических образов.

• 2.    Использование для получения промежуточных данных. Например, получив всего несколько значений (по одному для каждой группы) и зная вид закона распределения этих значений можно получить точный график распределения. Таким образом, можно снизить количество опытов по получению промежуточных точек.

• 3.    Использование при синтезе искусственных биометрических параметров. Знание закона позволяет создавать равномерно заполненные и сбалансированные базы тестовых образов.

Биометрические системы защиты информации с каждым годом становятся более популярными. Популярность биометрических систем объясняется удобством использования, то есть пользователь освобождается от необходимости запоминать длинные пароли или хранить ключи доступа в специальных сейфах. Ключом является сам человек: в любой момент, предъявив свою биометрию (палец, голос или подпись), пользователь может получить доступ к необходимой информации.

В настоящее время активно развиваются и рекламируются средства аутентификации, использующие статическую биометрию. К статическим биометрическим образам относят неизменяемые образы личности, данные ей от рождения и хорошо наблюдаемые окружающими (отпечаток пальца, форма ладони, рисунок вен, радужная оболочка глаза, форма лица и проч.). Основной недостаток использования статической биометрии состоит в том, что образы личности доступ- ны для наблюдения неограниченному кругу лиц и не могут быть изменены владельцем при необходимости (например при компрометации). Все это делает возможным изготовление хороших муляжей легальных пользователей и осуществление несанкционированного доступа путем предъявления системе муляжа. Именно поэтому для построения высоконадежных систем аутентификации рекомендуется использовать динамические образы человека: такие как особенности поведения, походки, рукописный или клавиатурный почерк, голос [4]. Динамическая биометрия сильнее статической из-за возможности сохранения в тайне ее образов и быстрой их смене при необходимости.

Несмотря на все преимущества динамической биометрии системы аутентификации на основе анализа подобных образов пока не получили широкого распространения. Это связано со сложностью создания подобных систем и отсутствием сертификатов для уже созданных. Сложность сертификации заключается с высокой стойкостью подобных систем к атакам подбора, например, заявляемая производителями стойкость программ аутентификации пользователей по тайным рукописным парольным фразам выше 1012, то есть злоумышленник должен предъявить 1012 рукописных образов для преодоления защиты. Следовательно, в дальнейшем при сертификации высоконадежной биометрии знания о законе распределения параметров помогут сократить объемы тестовых баз и повысить качество выдаваемых прогнозов. Выше было показано, что при описании распределений биометрических параметров можно исполь- зовать слегка измененные классические законы распределения. Так для описания распределения стабильности, уникальности и качества можно воспользоваться нормированным хи-квадрат распределением. Используя данное распределение при сертификации систем аутентификации по рукописным тайным паролям, следует учитывать, что для сильных систем (больших размерностей) можно пренебрегать дробной частью. Во время сертификации слабой биометрии необходимо использовать описание на основе теории фракталов.