Используемая система геодезических координат, проблемы и пути их решения

Точная пространственная информация необходима для решения различных задач в области экономики, обороны, транспорта, включая управления технологическими процессами, а также науку о Земле.

В настоящее время пользователи картографо-геодезическими данными и ГИС системами сталкиваются с рядом проблем, по крайней мере с тремя различными отсчетными системами. Топографические карты и координаты исходных пунктов государственной геодезической сети Республики Казахстан используют систему координат 1942 года (СК-42), и с другой стороны, при создании платформ геоин-формационных систем, а так же при решении различных практических задач по позиционированию, связанных с глобальной системой позиционирования (GPS и ГЛОНАСС), отдельные структуры (Организаций) предпочитают использовать геодезическую систему 1984 года (WGS 84). Кроме того, при решении задач глобального масштаба часто используют международную наземную систему отсчета (ITRS).

Хотя эти три системы отсчёта лишь незначительно отличаются друг от друга, но при решении точных и высокоточных задач на земной поверхности они существенно отличаются по конечными показателям, так как они были реализованы разными путями.

Использования различных систем отсчёта обусловлены тем, что поверхность Земли не представляют гладкую однородную среду. Океаны можно рассматривать как достаточно однородные, но поверхность или топография массивов суши демонстрируют большие неравномерности. Эти неравномерности делают невозможным приблизительное описание формы Земли, даже с помощью какой-либо достаточно простой математической модели. Исходя из этого, были установлены две основные опорные поверхности с возможностью приблизить форму Земли. Одна опорная поверхность называется геоидом, другая опорная поверхность-эллипсоидом. Они проиллюстрированы на рисунке 1 ниже.

Рис. 1. Поверхность Земли и две опорные поверхности, используемые для её аппроксимации: геоид и опорный эллипсоид. Отклонение между геоидом и эталонным эллипсоидом называется разделением геоида (Аномалия высот N)

Это обусловлено тем, что поверхность Земли совсем неоднородна. Можно было бы рассматривать поверхность морей и океанов как однородную поверхность, продолжая их под материками строить на основе этого подходящую модель, но по- верхность суши представляет собой достаточно сложную неравномерную среду. За счёт неравномерного распределения массы в теле, фигура Земли представляет очень сложную в геометрическом отношении фигуру (рисунок 2)

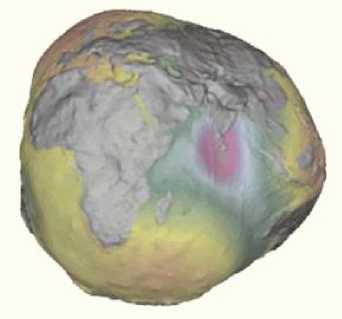
Рис. 2. Преувеличенный вид Земли, чтобы проиллюстрировать сложность его поверхности

Для того, чтобы решать различные математические задачи на поверхности Земли и в её теле, желательно иметь фигуру, у которой параметры её близки к характеристикам Земли, при этом это позволяло бы решать однозначные задачи на её поверхности. Такую поверхность можно было бы рассматривать так называемым геоидом. Даём определения к геоиду:

Геоид – это фигура, ограниченная невозмущенной поверхностью морей и океанов и продолженная под материками так, чтобы отвесные линии во всех её точках были перпендикулярны к ней [1].

Если это так, тогда поверхность геоида однозначна и теоретически можно её использовать для решения различных математических задач, так же рассматривать как поверхность для проектирования результатов картографо-геодезических работ. Но из-за неравномерного распределения масс в теле Земли и под влиянием различных физических явлений, поверхность геоида представляется неидеальной.

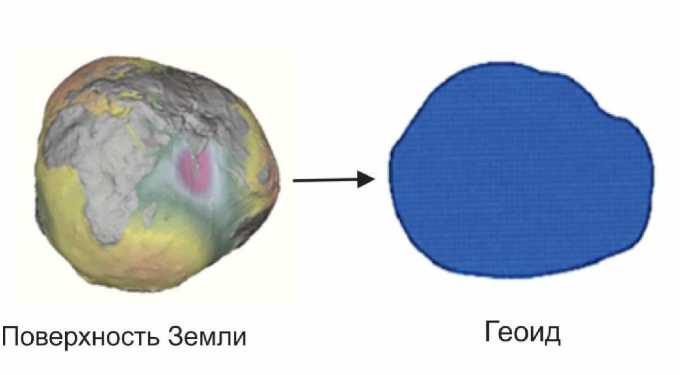
Рис. 3. Поверхность геоида

Используя различные измерения, в том числе методы спутниковой гравиметрии, а также, в зависимости от различных данных, таких, как время, густота гравиметрических измерений, способы математической обработки можно получить множество моделей геоида, каждая из них которая называется квазигеоидом или псевдогеоидом. В нашей стране, Республике Казахстан, для решения отдельных геодезических задач используется квазигеоид Молденского М.С. Полученная фигура квазигеоида по своей форме очень близка к Эллипсоиду, но по своей сути не может полностью обеспечить однозначного ре- шения задач. По этой причине использования фигуру эллипсоида как опорный поверхность является подходящим.

Эллипсоид

Для проектирования картографогеодезических данных наиболее подходящей поверхностью является сплюснутый эллипсоид (рисунок 4) . Это обеспечивает относительно простую фигуру, которая соответствует геоиду, в приближении первого порядка Эллипсоид образуется, когда эллипс поворачивается вокруг своей малой оси. Этот эллипс называется меридианным эллипсом.

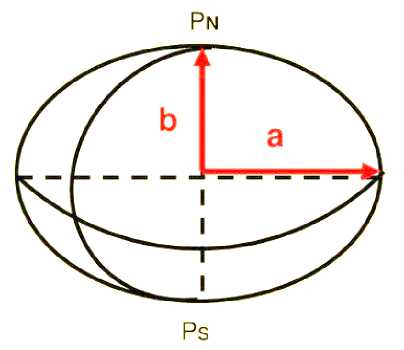
Рис. 4. Эллипсоид. Сплюснутый эллипс, используемый для представления поверхности Земли, определяемый его большой полуосью a и малой полуосью b

Эллипсоид - это фигура с известными геометрическими свойствами, основными параметрами которой являются:

a - большая полуось b - малая полуось а = (a-b)/a - полярное сжатие

Фигура эллипсоида дает возможность решать различные геодезические задачи и позволяет определять положение пунктов глобальной геодезической сети, расположенной по всей поверхности Земли. Эллипсоид, определенными параметрами позволяющий решать глобальные геодезические задачи, называют общеземным эллипсоидом. Положение общеземного эллипсоида подобрано таким образом, что его центр совпадает с центром масс Земли. Малая ось общеземного эллипсоида совмещается с положением оси суточного вращения Земли, условно принятым за исходную фундаментальную эпоху.[1] На основе общеземного эллипсоида строятся пространственные прямоугольные и эллипсоидальные геодезические системы координат.

В настоящее время в Республике Казахстан часто сталкиваются с двумя пространственными прямоугольными системами координат:

• 1.    WGS 84: a=6378137.0 метров, сжатия: α = 1/298,257223563. Общеземной эллипсоид разработанной Министерством обороны США.

• 2.    ПЗ 90: а = 6378136,5 метров, сжатия: α= 1/298,257839303. Общеземной эллипсоид разработанный в СССР и модернизированный Российской Федерацией.

Геоцентрические системы координат, построенные на базе указанных эллипсоидов, используются для решения задач навигаций и обеспечения работы спутниковых систем навигации (Позиционирования) GPS и ГЛОНАСС.

При создании топографических планов и карт, а также в ходе выполнения различных геодезических работ, практически невозможно на прямую использовать СК-84 и ПЗ-90, по этой причине каждое государство или группа государств создавали свою систему координат и референц-эллипсоид.

Форму, размеры и ориентировку референц-эллипсоида подбирали таким образом, что размеры большой и малой полуоси отличались от параметров общего земного эллипсоида, ось вращения и плоскости экватора референц –эллипсоида размещали параллельно к оси вращения и плоскости экватора Земли, в пределах территории страны или группы стран, отклонений поверхности референц-эллипсоида от геоида (квазигеоида) составляло наименьшими.

В нашей стране используется референц-эллипсоид     Красовского,     который характеризуется величинами [1]:

а = 6 378 245 м, a = 1: 298,3.

Положение (ориентировка) эллипсоида Красовского в теле Земли определено геодезическими координатами центра круглого зала Пулковской обсерватории:

широта В = 59° 46’ 18’’, 55, долгота L = 30° 19’ 42’’, 09, азимут направления на пункт Бугры А = 121° 10’ 38’’, 79.

Высота геоида над референц-эллипсоидом в Пулково принята равной нулю [1].

Принимая за основу данный референц-эллипсоид, для выполнения картографогеодезических работ, а также для решения различных инженерных задач использует зональную плоскостную систему координат 1942 года. Плоскостная съемка традиционно опиралась на воображаемую плоскую опорную поверхность, или систему отсчета (datum), с декартовыми осями. Эта прямоугольная система используется для описания измеренных данных в виде координат y и x. Несмотря на то, что поверхность земли имеет часть дуги эллипсоида, оно обеспечивало и продолжает обеспечивать адекватное расположение топографических объектов на воображаемую поверхность, для небольших территорий. Привязка высот к таким горизонтальным координатам в некоторой степени выражает топографическую неравномерность земли, но по мере увеличения площади система теряет точность.

Пункты государственной геодезической сети закреплены по всей стране в системе координат 1942 года и используется как основная, но в данное время не обеспечивает необходимую точность к геодезическим данным. Это связано с несколькими причинами:

• 1.    С момента принятия и до настоящего времени не уточнены её параметры;

• 2.    Координаты пунктов государственной геодезической сети были определены с использованием традиционной технологии (по точности и по достоверности зна-

• чительно отстает от современной технологии);

• 3.    При использования современных спутниковых и геоинформационных систем появляется необходимость постоянного пересчета и перевычисления;

• 4.    Имеется проблема несовместимости цифровых геопорталов, созданных на основе государственной системы координат Республики Казахстан с цифровыми порталами, созданными в мире.

Все выше перечисленные недостатки показывают, что дальнейшее использование СК-42 не может обеспечить потребности к точности геодезических данных на современном этапе, в будущем отрицательно будет сказываться на результаты картографо-геодезических работ. В связи с этим возникла необходимость модернизации или использования созданных, или создаваемых в мире систем координат как государственных.

С учетом растущей глобализации в мире, появилась острая необходимость на услуги более точного глобального позиционирования в мировом масштабе. Это подталкивает на то, что все геодезические и картографические работы, проводимые с целью создания пространственных данных, должны базироваться на глобальной геодезической системе отсчета, на основе общеземного эллипсоида. По этой причине Генеральная Ассамблея Организации Объединенных Наций приняла резолюцию о Глобальной геодезической системе отсчёта для устойчивого развития (A/RES/69/266) 26 февраля 2015 г. Целью настоящего документа является создание условий для государств при переходе в глобальную геодезическую систему отсчёта (GGRF). [2]

Исходя из вышеизложенного, для нашего государства открыто стоит вопрос о необходимости модернизации системы координат на базе референц-эллипсоида Красовского или перехода в другую систему отчётности и координат по следующим причинам:

• 1.    В случае использования в качестве государственной системы координат в какой-либо существующей в мире системе, появляются неудобства о невозможности

• 2.    При условии модернизации или обновления существующей государственной системы координат, появляется возможность дальнейшего использования имеющихся картографо-геодезических данных, что удобно для нынешнего времени, но в дальнейшей перспективе появляется проблема с несовместимостью с другими картографо-геодезическими данными и цифровыми порталами, созданными в мире [3].

полноценного использования имеющихся ранее созданных картографогеодезических данных;

Все это указывает на то, что несмотря на появляющиеся проблемы, которые будут выражаться виде перерасчётов и перепроектирования, необходимо использовать как государственную GGRF-Глобальную геодезическую систему отсчёта.

Атрибуты: ITRF-2008. Единица-метр. ITRF2008- Datum. Международная наземная система отсчета-2008 г. Эллипсоид-GRS 1980. Нулевой меридиан-Гринвич. Источник информации-Международная служба вращения Земли (IERS).

В качестве основы необходимо принять базовую поверхность WGS 84, параметры которой представляют собой эллипсоид с экваториальным радиусом a=6 378 137 м на экваторе и сжатием f = 1/298,257 223 563.

Особенностью ITRF2008 является то, что по сравнению с референцными СК-42 является геоцентрической:

– Начало системы координат совпадает с центром масс Земли

• –    ось Z направлена к условному земному полюсу;

• –    ось X направлена в точку пересечения начального (Гринвичского) меридиана и плоскости экватора;

• –    ось Y дополняет систему до правой [4].

Прогнозируется, что вследствие перехода появится масштабное изменение площадей, сдвиг координат точек на территории Республики в последствии переориентирован на пространственных данных.

Плоскостную зональную систему координат создать на поверхности эллипсоида GRS 1980. При этом сохранить деления поверхности эллипсоида на 6 градусных зон, начало отсчёта оставить от Гринвичского меридиана, в таком случае криволинейные координаты (долгота и широта) углов рамок трапеции государственных топографических карт остаются без изменений, только появляется сдвиг плоских координат х и у.

В результате решения данного вопроса появится возможность исключения несовместимости геопорталов, использования напрямую данных полученных со спутниковых, навигационных и других систем. В конечном счёте положительно будут сказываться на развитие экономики, науки Республики Казахстан.

Откладывание данного вопроса на перспективу несомненно приведёт к несовместимости цифровых данных, созданных за рубежом и к трудностям использования спутниковых и других высокоточных систем.