Исправление аномалий в графах реконструкции деревьев процессов Linux

Реконструкция дерева, процессов является ключевой подзадачей в системах сохранения-восстановления состояний Unix-подобных операционных систем с поддержкой многопро-цессности и разделения ресурсов [1]. Одним из универсальных способов реконструкции дерева, является построение частично упорядоченного множества, состояний, через которые должны пройти процессы, чтобы сформировать итоговое дерево в заданной конфигурации. По отношениям на. данном множестве формируются цепочки действий, восстанавливающих состояния процессов - цепочки системных вызовов. Целью работы является,

«Московский физико-технический иистритут (национальный исследовательский университет)», 2019

во-первых, демонстрация примера дерева процессов, на котором разработанные на данный момент алгоритмы [1-3], работающие в жадном предположении о подходящих состояниях для передачи атрибутов, строят некорректные промежуточные представления для реконструкции, обоснование причин такой аномалии с точки зрения вида частичной упорядоченности по зависимостям и внесение предложений по исправлению аномальных графов реконструкции [2,3]. Во-вторых, следует произвести оценку размера множества проходимых процессами состояний по отношению к множеству из входного дерева, что позволит как ответить на вопрос, насколько эффективно работает реконструкция, если дублировать состояния-носители с нужными для реконструкции атрибутами, так и привести практически более полезную оценку вычислительной сложности по размеру входного дерева.

2.    Предыдущие работы и основания исследования

В работах [2,3] были предложены алгоритмы, строящие графы реконструкции некоторых классов деревьев процессов за полиномиальное время. Алгоритмы представляют собой двухфазные анализаторы деревьев процессов, первой фазой которых служит LR-разбор входного представления как контекстно-свободного, с дальнейшим контекстным анализом на второй фазе: либо переписыванием результата разбора в специальной стеково-кадровой структуре данных [2], либо общими методами атрибутного анализа - переписыванием абстрактного семантического дерева, управляемым атрибутной грамматикой [3]. Результат такого разбора - промежуточное представление, включающее состояния процессов, которые следует воспроизвести для восстановления дерева, и отношения между состояниями. Семантика таких отношений - системные вызовы, переводящие процессы из состояния в состояние. Полученная конструкция может быть топологически отсортирована, и выполнение системных вызовов в порядке сортировки восстановит исходное дерево процессов из начального состояния - корневого init-процесса [2-4]. Далее будет показано, что существуют отдельные случаи, когда алгоритм [3] возвращает конструкцию, по которой невозможно восстановить дерево процессов.

С другой стороны, исследования корректности процедур восстановления деревьев, а также множеств состояний Linux-процессов как частично-упорядоченных относительно атрибутных зависимостей, заключают полурешёточную упорядоченность вершин орграфа реконструкции [5]. В разделе 3 данной работы демонстрируется связь аномалии алгоритма [3] с нарушением полурешёточной упорядоченности, а также обусловленность такого нарушения отступлением от общего случая построения полурешётки множества состояний. В разделе 4 предлагаются способы ликвидации такой аномалии добавлением необходимых состояний и доупорядочиванием.

3.    Анализ аномалий в графах реконструкции3.1.    Определения

Будем пользоваться определениями, введёнными в работах [4,5]. Рассматривается дерево процессов [2-5] - ориентированное дерево:

Т = (V,E),                                      (1)

а также орграф реконструкции дерева процессов [3-5] - промежуточное представление, по которому восстанавливается исходное дерево из некоторого начального состояния:

G(T ) = (V + ,E +),                                   (2)

где V + = V U V ^,н! - финальные вершины V, дополненные промежуточными V ^mt, соответствующие состояниям процессов в ходе выполнения системных вызовов, описываемых E + как переходами между состояниями и иерархическими зависимостями [3, 5]. В вершинах хранятся словари атрибутов состояний процессов:

Vv Е V + B v. attr : v.key = val(v .attr [key]) |' None', V key Е К, К список атрибутов процесса - идентификаторов, файловых дескрипторов, других описателей системных ресурсов, и val(v.attr[key]) : К ^ typed _val (key) - отображение таких имён на типизированные значения атрибутов. Вспомогательно вводится понятие множества вершин с равным значением атрибута u.attr₁:D(attr₁ ,u.attr 1 ) = {v Е V + |v.attr₁ = u.attr₁ }.

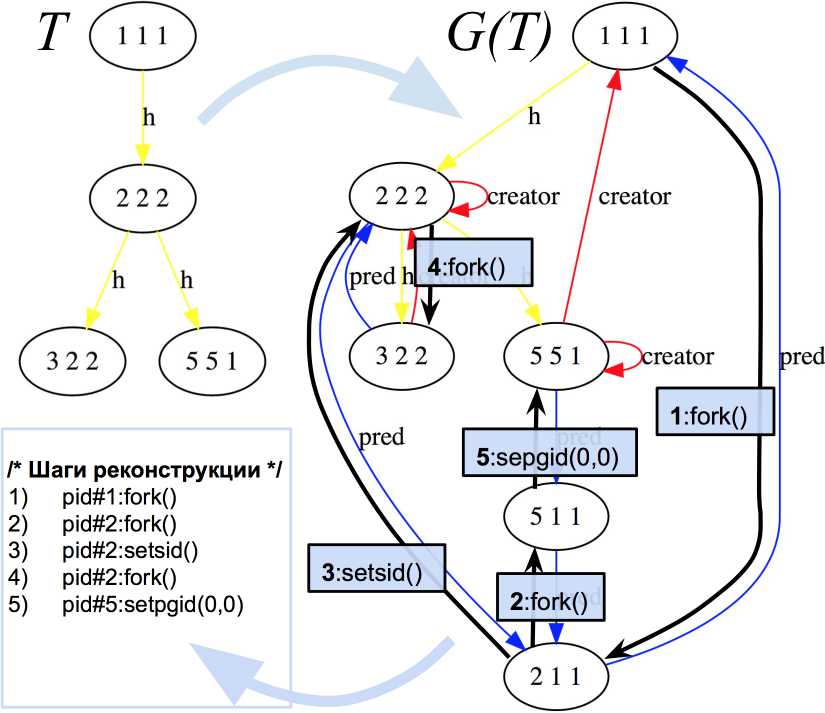
Рис. 1. Промежуточное представление - орграф реконструкции для атрибутов процесса, сессий и групп процессов G ( T ) некоторого дерева процессов Т, дополненный зависимостями между состояниями процессов. Исходные ребра иерархичности из Т выделены меткой «Һ»

Следует отметить свойства атрибутов образовывать иерархии.

Определение 1. Будем говорить, что attr₂ доминирует над attr1, attr₁, attr₂ Е К, если V u Е V + : V v Е D(attr₁ ,u.attr₁ ) ^ val(u.attr₂ ) = const.

Определение 2. Доминирующий над attr₁ атрибут attr₂ называется минимально доминирующим, если и только если V u Е V +B{v} Е V + : v.attr₂ = u.attr₂, VV' = {v} U v ', и V v ' Е V + \ {v} ^ v ' .attr₂ = const.

Пользуясь определением 2, можно описать множество минимальной мощности, включающее и множество состояний с различными значениями атрибута attn, но с идентичными attr2 и его замыкание.

Зависимость между состояниями u,v Е V + вводится в [5] как отношение (u, v) с семантикой «для реализации u требуется сначала реализовать v». Таким образом, если в некоторый момент в системе существует процесс в состоянии v, то выполнено необходимое (но не достаточное!) условие для реализации состояния u некоторого процесса, а зависимость называется разрешённой. Будем говорить, что зависимость происходит по атрибуту attr, если v либо создаёт атрибут attr, либо в его контексте происходит системный вызов, выставляющий данный атрибут в u. Зависимости определяют частичный порядок на V +, причём такой порядок - полная верхняя полурешётка [5].

Используя данное определение, рассморим ещё одно промежуточное представление.

Определение 3. Графом реконструкции, дополненным зависимостями, назовём ориентированный мультиграф G^dep:

G^dep(T ) = (V + ,Е ^dep U E ⁺),

где Е ^dep - множество зависимостей между состояниями процессов как вершинами.

При формальном анализе зависимостей в [5] вводится экстенсивный и монотонный оператор CL, смысл которого - определение множества состояний, на котором замкнуты действия с некоторым атрибутом.

Определение 4. Пусть CL(v.attr i ) : V ⁺ ^ V ⁺ - oneратор, Vv G V ⁺ определяющий f G V⁺ с минимальным доминирующим атрибутом для некоторого attr^. такой, что v U CL(v) = CL(v) = f. Если единственная неподвижная точка CL - состояние, в котором создан минимально доминирующий атрибут для attr, то CL - оператор замыкания. В противном случае назовём такой оператор оператором предзамыкания PCL.

Оператор PCL рассматривается для получения промежуточных носителей атрибутов, создателей атрибутов и определения состояний-предшественников. Ключевые свойства CL л PCL обсуждены в [5].

3.2.    Алгоритм атрибутной реконструкции [3]

Напомним основную процедуру алгоритма [3]:

function AGTTM (IR,Т,схр 1'):

Output: D for any Node in dfs(T.root) do cond = f (expr(Node.^ttr)-) // проверка текущей вершины и предка if cond not in IR then

// проверка жестко наследуемых атрибутов - сессий, пространств имён cond = upbranch(...) if not cond in IR then

// проверка выставляемых в поддереве атрибутов - групп процессов и др. cond = dfs(expr(Node, Current)) end

end

D = TR(D, Ex, IR, k(cond))- end return D.

Algorithm 4: Восстановление дерева процессов Linux трансформациями, управляемыми атрибутной грамматикой.

Алгоритм производит проход по всем вершинам входного дерева. Для каждой вершины и некоторых других вершин алгоритм сопоставляет атрибуты с шаблонами, называемыми «правилами вывода» (Inference Rules, IR"), запоминает вершины с атрибутами, подходящими под шаблон:

• 1)    если проверка родителя даёт наследование всех атрибутов, кроме идентификатора процесса, то произошёл вызов ’fork’;

• 2)    иначе, если атрибут жестко наследованный, как сессия, и не совпал с родительским, добавляются носители атрибута в цепочке от возможно добавленного создателя в процедуре ’upbranch’, выполняемой, в худшем случае, за O(|V ^intermediate l ) 6 O(|V ⁺|), V intermediate _ _теКущ_Ие состояния: входные и уже воссозданные в ходе работы;

• 3)    иначе, производится внутренний обход за O(|V^intermediate|) 6 O(|V ⁺|), в котором сопоставляются правила для атрибутов, выставляемых не только наследованием, как группа процессов.

Шаблонам проверки атрибутов соответствует системный вызов и трансформация дерева в результате его применения. Правила трансформации достаточно просты и не требуют применения методов проверки графовых изоморфизмов - на каждом шаге достаточно [3]:

• 1)    добавить отдельную промежуточную вершину - создатель или носитель атрибута, а в случае с жестким наследованием - цепь из таких вершин;

• 2)    добавить ребро - системный вызов, а в случае с жестким наследованием приписать соответствующий вызов каждому ребру цепи;

• 3)    возможно, добавить промежуточную вершину, перебросить иерархическое ребро и добавить ребро от вновь созданной вершины к текущей - добавить процесс-родитель взамен init-процесса - «обратный reparent» [2,3].

3.3.    Анализ особого случая дерева процессов

Корректность сопоставления шаблонов только по атрибутам следует из того, что алгоритм работает с корректными, то есть полученными из реальных снапшотов, деревьями: так, например, если найден создатель атрибута, состояние-носитель атрибута не может быть реализовано до него: это гарантируется невозможностью создать такое дерево процессов в ОС. Алгоритм корректно обрабатывает большое количество различных конфигураций деревьев процессов на практике [3], однако, как будет показано далее, существуют деревья, для которых жадный подход может приводить к некорректным графам реконструкции.

Рассмотрим следующее дерево процессов (рис. 2а): init-процесс, потомок которого имеет pid 2, pgid 3, и потомка, имеющего pid 3 и pgid 2. Все процессы лежат в едином пространстве имён процессов и единой сессии, созданной init-процессом.

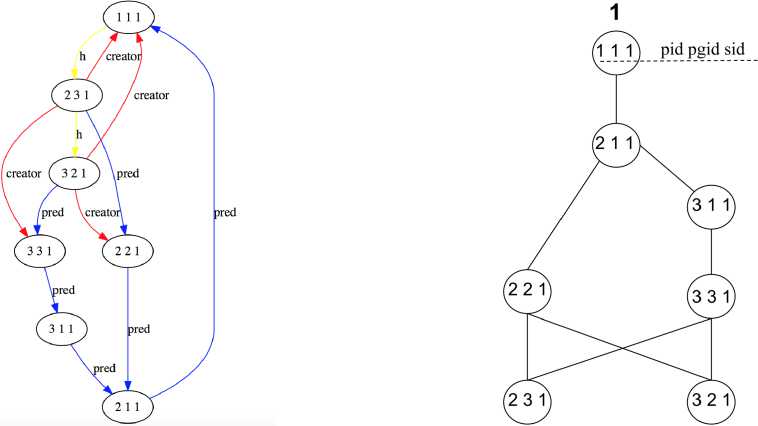
а)                                                       б)

Рис. 2. Граф реконструкции с зависимостями G^dep == (V+, Е + U Е^dep ) рассматриваемого дерева (а) и соответствующая диаграмма Хассе множества состояний процессов по зависимостям V +(б)

Запустим процедуру построения графа реконструкции по алгоритму [3]. Для каждой из вершин, встреченных во внешнем цикле, алгоритм будет совершать вложенный проход и искать подходящие по атрибутам вершины, определять места вставки промежуточных состояний и рёбер с системными вызовами между ними. Также будем сохранять восстановленные зависимости, которыми алгоритм неявно оперирует в сверке условий, налагаемых на атрибуты во вложенном обходе. В результате получим граф реконструкции с зависимостями G^dep, изображённый на рис. 2а.

Зависимости, разрешаемые в ходе построения G ^P разделяются на 4 типа и определяются соответствующими операторами предзамыкания и замыкания [5]:

• 1)    Зависимость от вершины-предшественника PCL(u,attr) _pTec i.

• 2)    Зависимость от вершины-создателя attr, PCL(u, attr) _crea t _or.

• 3)    Зависимость от вершины-исполнителя системного вызова, добавившего состояние с данным атрибутом PCL(u,attr) _sysca ii _er.

• 4)    Зависимость от минимально доминирующего атрибута для attr, C L(u,attr); в замыкании, задаваемом данным атрибутом, и происходят действия над attr следовательно, все образы, определяемые PCL, лежат в замыкании, определяемом CL. Рассматривается технически, и в дальнейших рассуждениях не участвует.

PCL(u,attr) _sysca ii _er задают отношения, соответствующие рёбрам, антинаправленным рёбрам системных вызовов в G, кроме того, можно считать, что PCL(u, attr) _sysca ii _er совпадают с PCL(u, attr) _pre a так как в случае с вызовами fork, setsid и setpgid процесс-предшественник, лежащий в замыкании по минимально доминирующему атрибуту - сессии в случае группы процессов, пространству имён процессов в случае сессии и номера процесса, имеет возможность самостоятельно выполнить действие по созданию потомка или выставлению собственного атрибута [7]. Таким образом, для анализа представленного примера достаточно рассмотреть разрешение зависимостей типа PCL(u, attr)_crea^_or и PCL(u, attr) _pre d.

Рассмотрим зависимости, разрешаемые при последовательной реконструкции вершин (231) и (321). Пусть сначала производится реконструкция (231), для которой требуется, чтобы в системе существовала группа процессов 3, что достигается наличием (331): PCL((231), attr)_crea^_or = (331), и найден предшественник PCL((231), attr)_pre^ = (221). При реконструкции (321) требуется, чтобы в системе существовала группа процессов 2, что достигается наличием (221): PCL((321), attr)_crea^_or = (221), и предшественник: PCL((321), attr) pr _e d = (331). Но в момент реконструкции (321) состоянием процесса 2 является состояние (231), и группы 2 уже не существует. Случай с реконструкцией (231) после (321) симметричен и также приводит к конфликту по зависимостям.

Построим диаграмму Хассе множества вершин V + как частично упорядоченного по зависимостям множества. Диаграмма, представленная транзитивным сокращением G^dep, изображена на рис. 26.

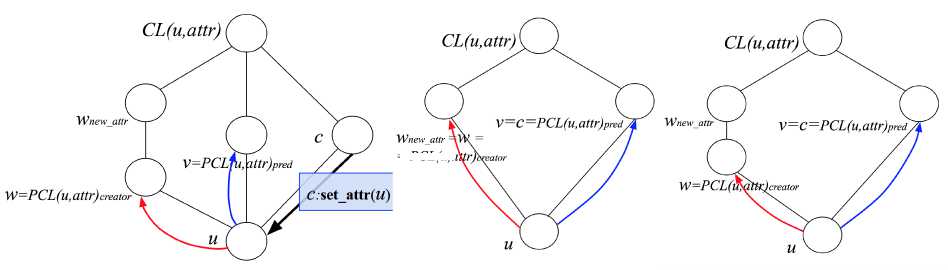
= PCL(u,a

а)                                           б)                             в)

Рис. 3. Общая схема реконструкции состояния u с атрибутом attr [5] (а), фактическая схема из алгоритма [3] (б) и вариант исправления (в)

Заметим, что диаграмма не является диаграммой полурешётки [6]: полурешёточ-ная упорядоченность нарушается на вершинах с атрибутами (221), (231), (331), (321). Действительно, (231) U (321) не определяется однозначно. При этом исключение любого из отношений между вышеуказанными состояниями, очевидно, приведёт к неразрешённости соответствующей зависимости, следовательно, к некорректности полученной конструкции.

Нарушение полурешёточной упорядоченности в данном примере связано с отступлением алгоритма [3] от общей схемы реконструкции [5] (рис. 3), когда для каждого атрибута, вообще говоря, должен существовать отдельный носитель - состояние создателя или отдельный процесс, которому предшествует создатель атрибута (рис. За, в), в то время как жадный алгоритм использует любую подходящую вершину, предшествующую целевой (рис. 36). Предложим два способа исправления данной неточности в разделе 4. Оба способа восходят к созданиям копий состояний с нужными атрибутами.

4. Поправки в процесс реконструкции Предложим вариатны исправления исходного G^ непосредственно на этапе построения. X р1[1]=2                 х р2[1]=3 (2 2 1) 91[1]=2            А о Л д2[1]=з Vy si[i]=i          у ° у s2[i]=i 6 зщ р1и]          6 2щ р2и] V У 91[2]=д2[1]        V 7 д2[2]=д1[1] s1[1]                              s2[1] а) Д р1[1]=2                х р2[1]=3 (2 2 1) ді[і]=2            Д о У д2[1]=з s1[1]=1                         s2[1]=1 .'4 2 1;     (23^) РШ1 x <    V У ді[2]=д2[і] S1[1] p4[1]=4 д4[1]=д1[1] s4[1]=s1[1] (Л 2 T) Р2И] Г 7 g2[2]=g4[1] s2[1] в) Д-Д p1[1]=2                  p2[1]=3 22 1 W2      УоДд2[і]=з S1[1]=1            У °ІД2[1]=1 i'4 2 1;                P1M1 /         (5 3 1 x <    V У g1[2i=92[1i       x s1[1] \ p4[1]=4                             \ д4[1]=д1[1] s4[1]=s1[1] (3 2 Ц p2[U V 7 g2[2]=g4[1] s2[1]

как на этапе пост-обработки, так и Д-Д р1[1]=2                  р2[1]=3 (2 2 1) д1[1]=2 X          А о У д2[1]=з s1[1]=1 \                     s2l1l=1 \     р4[1]=4\    / . ,д4[1]=д1[1] / /    \(s 4[1]=s1j1]y V у д1[2]=д2[1]         V 7 д2[2]=д4[1] s1[1]                              s2[1] б) Д-Д р1[1]=2                  р2[1]=3 (2 2 1) 91[1]=2            А о Л д2[1]=з хЛу S1[1]=1            к ° У s2[1]=1 У \ р4[1]=4 у '< р5[1]=5 i4 2 1 )g4[1]=g1[1]i5 3 1 , д5[1]=д2[1] x-.__Xs4[1]=s1[1]         s5[1]=s2[1] 3 Й РЯ1]                 2 Г) Р2П] V 7 д1[2]=д5[1]         V 7 д2[2]=д4[1] s1[1]                             s2[1] г) . р5[1]=5 / д5[Ц=д2[1] s5[1]=s2[1]

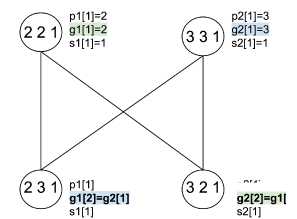
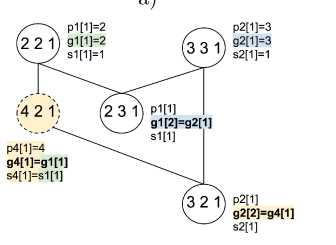
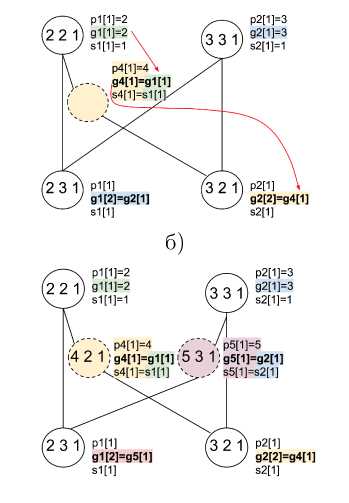
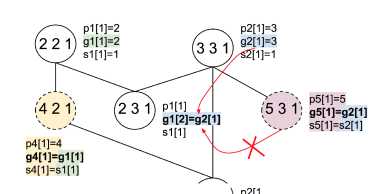
Рис. 4. Изменение конфликтного подмножества из примера раздела 3 анализом SSA-представления (а) - добавление носителя (б) и диаграмма Хассе полученного исправленного подмножества (в). Подмножество с избыточно созданными носителями (г) можно переупорядочить (д) и вложить в полурешётку, не нарушая её свойств

4.1. Анализ графа реконструкции, переведённого в SSA-форму

Из естественного требования, что в любой момент времени в системе может быть не более одного процесса с некоторым pid из одного пространства имён, следует, что множество состояний процесса - либо цепь в G ^dep, либо пустое множество. Следовательно, можно рассмотреть версионирование состояний для каждого из процессов: для каждого атрибута в цепи состояний, если его значение отлично от предшественника, нужно присвоить номер из некоторой возрастающей последовательности, а также отметить первое и последнее состояния. В результате получим представление (рис. 4а), называемое SSA (Single-Statement

Assignment [8]), в котором каждое новое значение присваивается уникальной переменной и лишь единожды. При этом переменным соответствуют атрибуты, а разбиение на уникальные переменные будет производиться по состояниям каждого из процессов на этапе пост-обработки G(T) ^dep, Сформулируем процедуру правки исходного графа: каждый раз, когда в некотором состоянии встречается атрибут с новым номером, для неё проверяется зависимость по данному атрибуту: если происходит присваивание значения из создателя, следует встроить промежуточную вершину-носитель, к переменной которой присваивается исходное значение, а затем из данной переменной присваивается в целевую вершину.

function Gdep2SSA (G^dep,K );

Input : G^dep. K

if isCreator(PC L(proc, attr) _creator, attr) then

// в модифицированном графе значение может передаваться через носитель, creator - наследованное название addNode(Gdep,from=PCL(proc, attr )creator, to=proc)

end end end end end return Gdep:

Algorithm 5: Gdep2SSA - алгоритм правки графа реконструкции с зависимостями переводом в SSA-представление.

Процедуры, создающие новую переменную, добавляющие вершину между создателем и целевым состоянием и проверяющим создателя - addNewVar, addNode, isCreator, а также вычисление нужных PCL, обладают сложностью 0(1) как по времени, так и по памяти, ввиду того, что вся необходимая информация уже хранится либо в G^dep, либо в счётчиках i, epoch и извлекается также за 0(1). Кроме того, состояния по-прежнему хранят только текущее значение атрибута, и для каждого атрибута исправление добавляет не более одной вершины в граф, следовательно, сложность по памяти остаётся О(|V ⁺|), если атрибутов много меньше числа вершин. Извлечение цепей состояний getChains с одинаковым pid может производиться обходом в глубину от init-процесса антинаправленно рёбрам предшествования [9], а храниться - как 2 указателя для каждой цепи - на начало и конец. Следовательно, сложность по памяти с учётом исправлений составляет О(|V ⁺|), как и у исходного алгоритма [3]. Сложность по времени возрастает на О(|V ⁺|), так как добавленные вершины не требуют исправления, то есть итоговая сложность составляет О(|V ⁺|²), как у исходного алгоритма.

На практике процедуру добавления не требуется выполнять для каждого состояния. Так, конструкция на рис. 46, в уже корректно исправлена добавлением вершины 4. Конструкция с исправлениями для всех атрибутов группы избыточна (рис. 4г), однако её, очевидно, можно переупорядочить и вписать в исходную полурешётку (рис. 4д): зависимости уже «избыточно» удовлетворены, и некоторые из них могут быть исключены без нарушения разрешимости, то есть формально полурешёточная упорядоченность V+ соблюдается.

Возможны две основные стратегии внесения поправок:

• 1)    перевод в SSA всего графа реконструкции. Может давать избыточные носители;

• 2)    перевод в SSA подграфов, изоморфных характерным нарушениям полурешётки, как в примере раздела 3. Более математически изящный способ внесения поправок: гарантирует отсутствие избыточных носителей в подграфах, неизоморфных аномальным подграфам, но потребует проверку орграфов на изоморфизм, что может составлять квадратичную сложность по памяти и, по меньшей мере, квадратичную, а в некоторых случаях и экспоненциальную сложность по времени.

4.2. Принудительная передача атрибута через носитель 5.    Оценки роста числа состояний

Альтернативой переходу в SSA-представление и усложнения пост-обработки графа реконструкции является возможность требовать для каждого найденного атрибута отдельного носителя, причём идентификаторы процесса носителя и создателя должны быть различны. Все носители должны быть завершены по окончании выполнения восстановления дерева, как промежуточные процессы. Такая, на первый взгляд, неоптимальная реконструкция гарантирует правильную упорядоченность цепи wnew, w, и (рис. За, в). В разделе 5 будет доказано, что принудительное создание отдельных промежуточных носителей увеличивает количество вершин, обрабатываемых при восстановлении не более чем в константу раз относительно мощности V.

Алгоритм [3] строит граф реконструкции за O(|V + |2) по времени для групп процессов, сессий и любых других атрибутов, требующих малое число вложенных проходов по сравнению с числом вершин. Исправление переводом в SSA приводит к такой же сложности. Однако представляют интерес временные оценки от |V| как количества вершин во входном дереве процессов, по которым и можно априорно оценивать время работы алгоритма. Покажем, что |V +| для любых корректных входных деревьев с группами процессов и сессиями - той же степени, что и |V|, то есть по размеру входного множества оценка также квадратична.

Теорема 1. Если VG(T ) = (V + ,Е+) :Т = (V, Е ) - корректное дерево процессов с атрибутами {pid,sid,pgid}. пго |"jyq| 6 0(1).

Доказательство. Пусть |V| = N. Для каждого процесса рассмотрим атрибут группы процессов, выставляемый в поддереве, и жестко наследуемый атрибут сессии. Нужно добавить к V носители и создатели различных атрибутов C _s и C g, которые будут использоваться в V _s ii V g. которых, в худшем случае, не более N [4]:

|V ⁺| =N + |C_S| + |Cg | + |V_S| + \ Vg | 6 3N + |C_S| + |Cg |.

Для реконструкции группы процессов нужен создатель, лежащий в одной с целевым состоянием сессии, и, возможно, отдельный носитель. Создатель и носитель группы «1» уже создан - это корневой процесс. Таким образом, |Cg| 6 2(N — 1). Рассмотрим передачу атрибута сессии процессу. Пусть Зг, и Е V ⁺ : v.sid == u.pid. Любой атрибут сессии, отличный от собственного, нужно наследовать, то есть для любого процесса ж в цепочке между и и г существует такое состояние, что x.sid = u.pid. Пусть 1(г,и) - длина цепи от и к г, a d(T ) -высота дерева Т. Очевидно, 1(г,и) 6 l(r,root) <  d(r), то есть требуется дополнительно не более (d(r) — 1) промежуточных состояний для наследования сессии. Тогда

|(А| 6 £ l(r,root) 6 |V_S|(d(T) — 1).

^ E V s

Сессия, отличная от наследованной, выставляется лишь единожды, поэтому можно исключить такие процессы из требующих дополнительных - они сначала переносят чужую, а затем создают свою сессию, откуда следует более точная оценка |I4| = (N — d(T ) — 1):

|C_S| 6 (N — d(T) — 1)(d(T) — 1) = Nd(T ) — d²(T) + 1.

Заметим, что d(T ) 6 (N — 1). слелователыю.

|C_S| 6 (N(N — 1) — (N — 1)² + 1) = N² — N — N ² + 2N — 1 + 1 = N,

|V +|   3N + 2(N — 1) + N    O(N )

ТЩ ⁶------ N ------~ O(N) ~ ^O(1).

6.    Заключение

Рассмотренные в работе способы внесения исправлений позволяют ликвидировать аномалии, связанные с нарушением полурешёточной упорядоченности, вносимые в процесс реконструкции деревьев процессов жадными методами поиска промежуточных состояний. При этом число промежуточных состояний для основных типов атрибутов увеличивается не критично, что практически важно. В дальнейшем следует привести строгое обобщение теоремы 1 на случай других атрибутов: дескрипторов межпроцессного взаимодействия, сигналов, пространств имён, отличных от пространства процессов. Представляет интерес также проведение экспериментов на различных наборах нагрузок: то, что аномалии в деревьях - статистически редкое событие, было проверено на синтетических тестах [2, 3] и требует дополнительных экспериментов на различных профилях нагрузки в реальных системах.

Работа выполнена при поддержке Егора Горбунова (Acronis), впервые обнаружившего и предоставившего рассмотренный тестовый пример.