Исследование алгоритма декорреляции сетевого трафика на основе вейвлет преобразования

За 2022 год более 82 процентов Интернет-тра-фика составила передача видео [1], что существенно превысило показатели предыдущих годов, даже с учетом взрывного роста видео-трафика в период пандемии. Исследования видео-трафика в сетях передачи данных начались еще в 80-х годах прошлого века. Еще в [2] были обнаружены ярко выраженные корреляционные свойства трафика, порождаемого видео с отсутствием резкой смены кадров и динамичных сцен (запись интервью, диктор телепрограммы). В [3] было показано, что экспоненциальная автокорреляционная функция, как и коэффициент вариации и вид распределения интервалов времени, характеризующих видео-трафик, является одним из важнейших параметров для описания трафика VBR-видео (Variable bitrate).

Существует несколько основных видов моделей, описывающих видео-трафик, среди которых можно выделить [4–7]:

• 1.    Авторегрессионные модели (AR).

• 2.    Модели на основе марковских процессов.

• 3.    Самоподобные или FARIMA (Fractal Auto-Regressive Integrated Moving Average).

• 4.    Вейвлет-модели.

• 5.    Остальные подходы, которые базируются на вероятностных распределениях, системе массового обслуживания M/G/∞, процессах преобразования и расширения выборки TES (Transform-Expand-Sample) и т.д.

Исследованию вероятностно-временных характеристик видео-трафика на основе указанных моделей посвящено достаточно большое количество работ, например [8–10], анализ корреляции можно найти в [11–13]. В большинстве из указанных публикаций автокорреляция интервалов времени связана со снижением качества обслуживания и уровня пользовательского восприятия. В связи с этим задача снижения уровня автокорреляции в видео-трафике представляется достаточно актуальной. Данная статья посвящена одному из методов снижения автокорреляции, который может быть применим не только для видео-трафика.

Исследование уровня автокорреляции при передаче видео в локальной сети

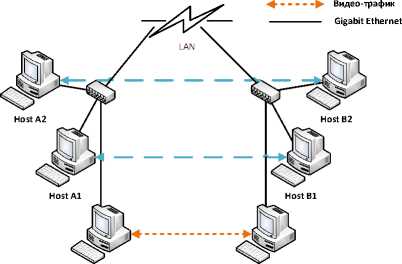
Было поставлено два эксперимента. В первом эксперименте видео передавалось между сервером и клиентом VLC (VLC ver. 3.0.21), при этом входящего и исходящего трафика хостов A1, A2, B1, B2, находящихся в подсетях сервера и клиента, не было. Во втором эксперименте при передаче того же видео на хостах в подсетях сервера и клиента были включены генераторы трафика HTTP Packet Sender, имитирующие работу взаимодействующих web-серверов. Трафик на сервере и клиенте фиксировался при помощи WireShark 4.2.7. Схема сети представлена на рисунке 1.

В первом эксперименте средняя задержка при передаче видео составила 0,217 c, уровень потерь пакетов составил менее 0,001% пакетов, коэффи- циент автокорреляции интервалов времени между пакетами на выходе видеосервера составил P1 = 0,0094, что позволяет утверждать, что автокорреляция интервалов времени между пакетами практически отсутствует.

Трафик между Web-серверами

VLC Video Server

VLC Video Client

Рисунок 1. Схема сети

Во втором эксперименте средняя задержка возросла до 0,381 с, уровень потерь возрос до 0,09% пакетов, а автокорреляционная функция интервалов времени между пакетами на выходе видеосервера представлена на рисунке 2.

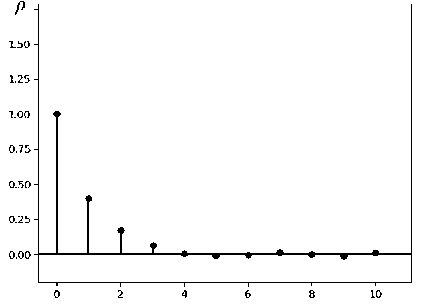
Рисунок 2. Автокорреляция интервалов времени на выходе видеосервера

На рисунке 3 изображена гистограмма интервалов времени между пакетами на выходе видеосервера для второго эксперимента.

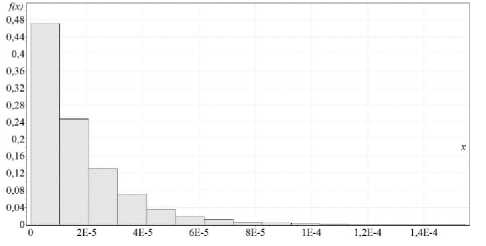
Рисунок 3. Гистограмма экспериментальной последовательности

На основе вышеизложенного можно утверждать, что увеличение задержки и повышение уровня потерь пакетов тесно связано с увеличением значения коэффициентов автокорреляции интервалов времени.

Моделирование последовательности с заданным коэффициентом корреляции

Для исследования метода снижения автокорреляции в последовательности интервалов времени, характеризующих реальный трафик, сгенерируем такую последовательность, имеющую показательное распределение с заданным коэффициентом корреляции, что позволит нам проанализировать различные случаи, в том числе, когда коэффициенты корреляции значительно выше значений, полученных в результате эксперимента. Моделирование такой последовательности т ( n ) осуществляется следующим образом:

^{т ( n} ) = £^{( n} ) + ^ 2^{( n} ) =

= ^c 0 ²

(41 - r² x ( n ) + r ^ 1 ( n - 1)) 2 + + (/1 - r² x 2 ( n ) + r ^ 2 ( n - 1))²

где x ₁ ( n ) и x ₂ ( n ) – последовательности независимых нормальных случайных чисел с нулевым средним и единичной дисперсией:

• ^ 1 ² ( n ) = c 0 (^1 - r² x ( n ) + r £ ( n - 1))² ,

^ ^{( n} ) = ^c 0 ('I^{1 -} r^{2 x} 2 ^{( n} ) ⁺ ^2 ^{( n - 1)) 2} , r ² = P 1 . [14].

Гистограмма смоделированной последовательности представлена на рисунке 4.

Автокорреляционная функция смоделированной последовательности при ρ ₁ = 0,95, что значительно превосходит ρ ₁ = 0,62, полученные при проведении эксперимента, представлена на рисунке 5. Последовательные значения коэффициентов автокорреляции при этом равны

ρ ₁ = 0,9534, ρ ₂ = 0,9102, ρ ₃ = 0,8693, ρ ₄ = 0,8288, ρ ₁ = 0,7535 и т.д. Представляется более актуальным исследовать именно эту последовательность, обладающую более значимыми коэффициентами автокорреляции.

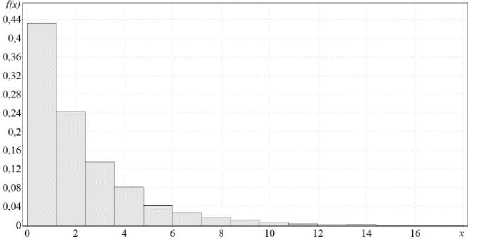
Рисунок 4. Гистограмма смоделированной последовательности

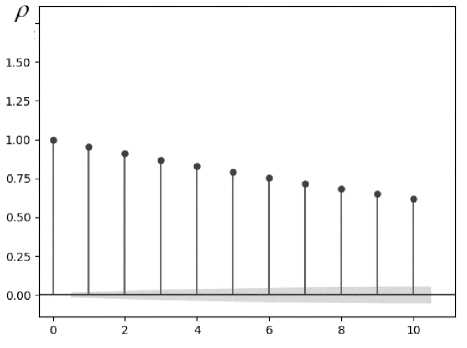
Рисунок 5. Автокорреляционная функция смоделированного распределения

Декорреляция интервалов времени

Воспользуемся способом, предложенным в [15]. Разобьем рассматриваемую последовательность отсчетов трафика на подгруппы, содержащие в каждой по 2 ^k элементов. Каждая такая группа будет являться кусочно-постоянной функцией, заданной на разбиении отрезка [0,1] на 2 ^k отрезков длины 2^{- k} . Таким образом, получим функцию f = { f s } , 0 <  s <  2 k - 1 . Представим ее как:

k -1 2 i -1

f=d+EE j л(x), i=0 j=0

где W j i ( x ) - вейвлет Хаара, который определяется как:

W оо⁽ x ) = W ⁽ x ) =

1, x e [0,12) -1, x e [1/2,1) ’ при i = 0, а для других значений i, j Wj i (x) по— лучаются путем сдвига и сжатия:

i

W _Jt( x ) = 2 2 w (2 i x - j ), j = 0,2 i - 1 .

Таким образом, для декорреляции исходной временной последовательности f = { f s } ,0 - ^s - 2 k — 1 необходимо найти значения коэффициентов d и c j , 0 - j — 2 ¹ - 1, i = 0,..., k - 1:

1                        1 2 ^k -1

d=J f(x) dx = г E fs,(1)

• ¹                                1 2 ^k -1

cj =f f(x > ji(x)dx = Г E f^ ji(x).(2)

В результате значения новых интервалов времени, определяемые коэффициентами cij, 0 ≤ j ≤ 2i-1, i = 0, ..., k-1, будут соответствовать де- коррелированной последовательности интервалов времени. Причем в данном случае вместо коэффициента d , вычисляемого по соотношению (1), можно для ускорения вычислений выбрать значение d в виде числа, соответствующего услоВию d > |cj.min .

Определение коэффициентов

Рассмотрим определение значений коэффициентов при k = 3. Выражение (2) при данном k примет вид:

(0.25,2) (0.375,2)

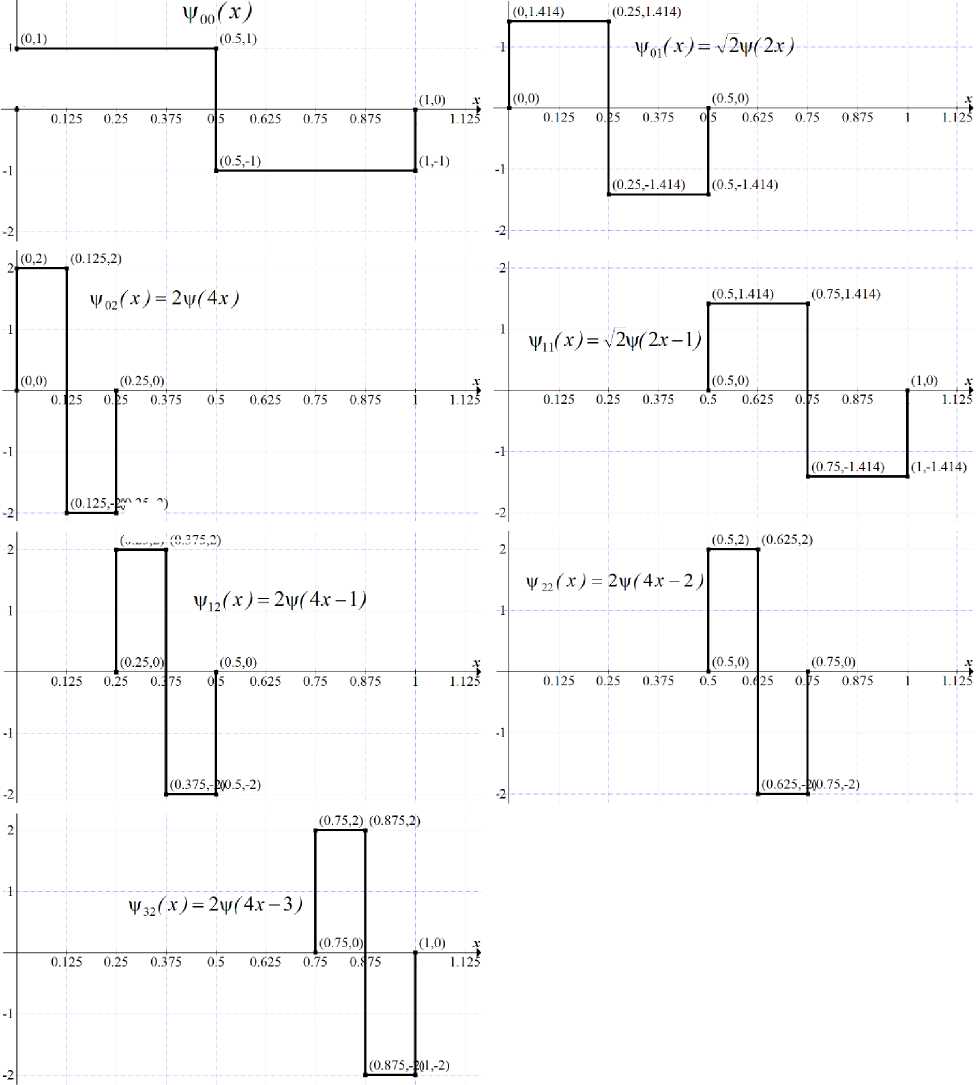
Риcунок 6. Вейвлеты Хаара

(0,0)

№>.25,-2)

C j = 7 f(0) ^ j (0) + f O M -O + - + f (W?) 8 [                        8                  8

где j = O, . ,2 ' - 1, i = 0,..., k - 1.

На рисунке 6 изображены вейвлеты, полученные для k = 3. Всего при k = 3 существует 7 функций на интервале [0,1] . Выпишем далее каждую из них:

W oo =[1, 1, 1, 1 - 1 - 1 - 1 - 1], m01 = [V2, V2, - V2, -V2, o, o, o, o],

Mo2 =[2, - 2, O, O, O, O, O, O],

M 11 = [ o, O, O, O, V2, V2, - V2, - V2 ] ,

M12 =[o, O, 2, - 2, O, O, O, O],

M22 =[O, O, O, O, 2, - 2, O, O],

M32 =[O, O, O, O, O, O, 2, - 2].

Поскольку в данном случае при k = 3 существует всего 7 вейвлет-функций Mji (x), коэффициентов nj будет тоже 7. Если рассмотреть значения п : j c1o = Е fM o1( n) = Т7т( fo + f - f2 - f3),

8 n=o c2O = Е fMO2( П ) = ( f) - f. ) ,

• 8 n=O

• C11 = Е f>n( n) = tx( f4+ f5- f6- f7), 8 n=o

то можно прийти к выводу, что любое из них может оказаться отрицательным. Поэтому использование константы d, удовлетворяющей условию d > |c . |, необходимо во избежание получения отрицательных значений декоррелированной по- следовательности.

Поступая аналогичным образом, можно определить коэффициенты для любого значения k > 3.

На рисунке 7 представлен результат декорреляции смоделированной последовательности интервалов времени ( ρ 1 = 0,95) при k = 3. Последовательные значения полученных коэффициентов автокорреляции при этом будут равны ρ 1 = 0,0622, ρ 2 = 0,0615, ρ 3 = 0,0489, ρ 4 = 0,0419, ρ 5 = 0,0488 и т.д.

Результат декорреляции той же последовательности при k = 4 представлен на рисунке 8. Последовательные значения полученных коэффициентов автокорреляции при этом будут равны ρ ₁ = -0,0067, ρ ₂ = -0,00765718, ρ ₃ = -0,0117, ρ ₄ = -0,012, ρ ₅ = -0,0127 и т.д. и т.д.

Таким образом, предлагаемый алгоритм декорреляции существенно снижает автокорреля- цию временных интервалов до значений меньше 0,02, что может говорить о полном ее отсутствии.

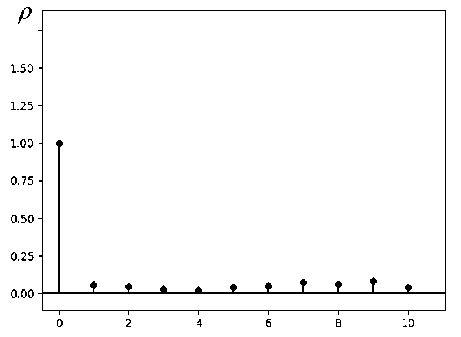
Рисунок 7. Автокорреляционная функция полученных интервалов времени при k=3

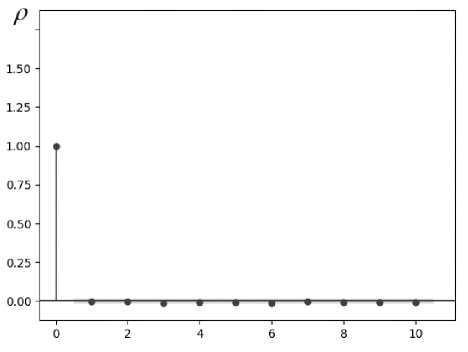
Рисунок 8. Автокорреляционная функция полученных интервалов времени при k=4

Заключение

Исследование показало, что интервалы времени между пакетами в сетевом трафике при передаче видео могут обладать автокорреляционными свойствами. Причем присутствие такой автокорреляции тесно связано с увеличением задержки пакетов и уровнем их потерь. Предлагаемый авторами алгоритм декорреляции может существенно снижать значения коэффициентов автокорреляции интервалов времени между пакетами в сетевом трафике. Дальнейшая работа по тематике статьи связана с программной реализацией предлагаемого способа непосредственно в драйвере сетевого устройства.