Исследование алгоритма Крона и его модификации при различных исходных данных

Автор: Кобак Валерий Григорьевич, Титов Дмитрий Вячеславович, Золотых Олег Анатольевич

Журнал: Вестник Донского государственного технического университета @vestnik-donstu

Статья в выпуске: 8 (69) т.12, 2012 года.

Бесплатный доступ

Рассматривается задача распределения множества заданий между устройствами однородной вычислительной системы по минимаксному критерию. Приводится постановка задачи, в которой подробно описываются объект исследования и принципы его функционирования. Для решения поставленной задачи предлагается использовать приближённые алгоритмы. Рассмотрены классический и модифицированный алгоритмы Крона и способы их улучшения за счёт формирования начального распределения заданий между устройствами вычислительной системы. С этой целью используются алгоритм критического пути и алгоритм Пашкеева. Для оценки эффективности полученных модификаций алгоритма Крона в работе приведены выходные значения ряда вычислительных экспериментов при различных входных параметрах. Эффективность модифицированных алгоритмов оценивалась по времени работы и отклонению полученного значения загрузки от оптимального значения. Разработаны программные средства для анализа эффективности модифицированных алгоритмов.

Еще

Алгоритм крона, модификация алгоритма крона, минимаксный критерий, начальное распределение, балансировка загрузки, вычислительная система

Короткий адрес: https://sciup.org/14249943

IDR: 14249943

Текст научной статьи Исследование алгоритма Крона и его модификации при различных исходных данных

Введение. В настоящее время широкое распространение и развитие получили вычислительные устройства с многоядерной архитектурой процессора и многопроцессорной архитектурой. Причём такие устройства могут входить в состав многомашинных комплексов, позволяющих решать сложные задачи путём распределения вычислительного процесса между ресурсами (ядрами процессора, процессорами, узлами многомашинного комплекса). Это позволяет значительно сократить временные затраты. Однако в процессе распараллеливания вычислений может возникнуть дисбаланс в загрузке доступных вычислительных ресурсов: часть устройств может простаивать, а другая часть будет загружена на сто процентов. Это приведёт к неэффективному использованию оборудования и, как следствие, к увеличению времени решения вычислительной задачи [1]. Поэтому особую важность представляет равномерное распределение нагрузки на все вычислительные ресурсы (приборы, устройства).

Постановка задачи. Пусть имеется многомашинная вычислительная система (рис. 1), состоящая из п идентичных параллельно функционирующих устройств (ЭВМ) Р = ^р_х,...,рД.

В ходе работы в систему поступает m независимых заданий Q = ^q_v...,q_m^, которые распределяются между процессорами и обрабатываются параллельно. Причём известно время выполнения >го задания f на любом из процессоров вычислительной системы, где j = 1, m . В каждый момент времени отдельный процессор обслуживает не более одного задания, которое не передаётся на другой процессор. Задача распределения сводится к разбиению исходного множества заданий на п непересекающихся подмножеств. Критерием разбиения, обеспечивающим оптимальность распределения по быстродействию, служит минимаксный критерий. Он определяет такое распределение заданий по процессорам, при котором время загрузки Т параллельным заданием минимально.

На рис. 1 приведено схематичное изображение многомашинной вычислительной системы, на вход которой поступает множество заданий, и множество значений времени выполнения каждого задания. Необходимым условием эффективного функционирования такой системы является равномерная загрузка всех вычислительных устройств, поэтому важную роль в такой системе играет балансировщик. Это устройство при получении входных параметров (множества заданий и множества значений времени выполнения) распределяет задания между устройствами вычислительной системы (создаёт баланс загрузки) по заданному алгоритму.

Рис. 1. Схематичное изображение многомашинной вычислительной системы

Алгоритм Крона. Для решения однородной минимаксной задачи можно использовать приближённые алгоритмы, которые позволяют получить решение, близкое к оптимальному, за меньшее время (по сравнению с точными алгоритмами).

Одним из таких алгоритмов является алгоритм Крона. Его применение обеспечивает случайное распределение множества заданий на множество приборов, вычисление времени загрузки каждого прибора {Т}(/ = 1,..., л) и обмен заданиями между приборами с максимальным Ттах и минимальным 7™|П значениями из набора {Т} при выполнении условия l^max _ ^min| < д, где Д = Ттах - Г"1, k, j= 1,2 ..., m.

После каждой операции обмена значения {Та} пересчитываются, выбираются новые два прибора с Т^тах и Т™, и процесс проверки указанного выше условия повторяется. Если условие ни разу не выполнится, алгоритм завершается [2]. На рис. 2 приведена схема итерационного процесса выбора пары заданий для последующего обмена по классическому алгоритму Крона.

Также авторы предлагают рассмотреть алгоритм Крона, который модифицирован следующим образом. Сначала множества заданий распределяются по классическому алгоритму Крона. Затем они дополнительно уточняются посредством обмена заданиями между приборами с максимальным Ттах и очередным Г'значением из набора {Т}. При этом выполняются условия:

^max > qj

Qk - Qj < Д, где tf^axe7™, qieT, Д = Т^тах- Т, к, j= 1, 2 ... m, i = 1, 2 ..., п.

После каждой операции обмена значения {Т} пересчитываются, выбираются новые два прибора с 7тах и Т, и процесс проверки указанного выше условия повторяется. Если сравнение с Ттах проведено для каждого Т и условие ни разу не выполнилось, то алгоритм завершается. На рис. 3 приведена схема итерационного процесса выбора пары заданий для последующего обмена по модифицированному алгоритму Крона.

Р2

рз

Р1

' Р”

рЗ

ill

121

131

11J

ОI

131

tl I

121 131

112 122

132

Н2

122

132

112

122

132

ИЗ 123 133 ПЗ

123

133 из

123 I

133

114 134

115

114 134

115

114 134

115

фтм

•ртая •

"pros

'plW

*ртй

111 >121 и til - 121 < А

111 >122 и 111 - 122 < А

til. > 123 и til — 123 < A

1*1

р2

1>3

р2

1*3

1 pl

I*³

121

131

til

121 131

111 121 131

112

122

132

112

122 132 И 2 122 132

ИЗ 123 133

U4 134

115

ИЗ

114

115

123 133

134

113 1123 133

114 134

115

"роад

Т*

| piisx'

^mN

tlZ > t21 И 112 "*■ t21 < X

112 > 122 и 112 - 122 < Д

t!2 > 123 и tl2— 123 < Д

Рис. 2. Схема итерационного процесса выбора пары заданий для последующего обмена по классическому алгоритму Крона

I”	pl		рз		pl	Pl		p3		pl		p2		P³
111	121	131			Hl	121	131			til	121 Bl
112	122	132			112	122	132			112		02	132
113 123 133 ИЗ						123	133 113					123	133
114 134 115					114 134 115					11 1 115			134
^rhtx	T₂		Tf"		y^max	Т»		T,^		T^		т_г
til >121 и til - 121 < A				I	11 >122 и til-122<Д				1	H>t23n til-123 < A

1 pl	p2			p3	pi		p2	\|>3	[pi__L	\|l2		p3
Hi	12 i		13!		Hi		121	131	Ш	121		131
	122		B2		112		02 ^:	132	112 \|	122	132
113	123		133		U3		123	133	113	123	133
114			134		114			134	114		134
115					0 5				115
1 _T «X				T™	"T BMX ⁴ J			T,™	1T-"™ I	T,		Tgr™®
tl2>t21n tl2-		121 < A			tl2>	122 и H2-t22			tl2>t23n tl2-L		13 <	A

Рис. 3. Схема итерационного процесса выбора пары заданий для последующего обмена по модифицированному алгоритму Крона

Улучшение алгоритма за счёт модификации начального распределения заданий. Авторы предлагают улучшить классический алгоритм Крона и приведённую выше его модификацию. Начальное распределение заданий будет выполняться с помощью алгоритма критического пути (СРМ) и алгоритма Пашкеева. Ранее, при исследовании классического и модифицированного алгоритмов Крона начальное распределение множества заданий формировалось посредством случайного распределения заданий по приборам. Таким образом, в результате сочетания классического и модифицированного алгоритма Крона с алгоритмами критического пути и Пашкеева получены новые модификации, экспериментальное исследование которых приведено ниже [3].

Проведение вычислительных экспериментов, направленных на получение статистических данных о работе каждого из алгоритмов, позволит выявить эффект (положительный или отрицательный) в произведённых модификациях алгоритма Крона. Входные данные для проведения экспериментов: п — количество устройств, m — количество заданий, Zi—z2 — диапазон генерации времени загруженности прибора (t7 e[zlzz2]). В ходе экспериментов случайным образом сгене рированы по 100 векторов загрузки, содержащие задания в диапазоне [zv z2]. Они были преобразованы в соответствие с алгоритмом критического пути и Пашкеева. Полученные результаты усреднялись по количеству экспериментов. В табл. 1 и 2 представлены результаты экспериментов для диапазона заданий 25—30.

Таблица 1

Усреднённые значения критериев

п	m	Значения исследуемых критериев
п	m	Opt	Крона и СРМ	Time (Крона и СРМ)	Крона и Пашкеева	Time (Крона и Пашкеева)
6	32	147,129	155,201	0,172	155,231	0,218
8	32	110,485	110,443	0,156	110,452	0,031
12	32	73,844	81,346	0,126	81,423	0,157

Таблица 2

Усреднённые значения критериев

п	m	Значения исследуемых критериев
п	m	Opt	Модификация Крона и СРМ	Time (модификация Крона и СРМ)	Модификация Крона и Пашкеева	Time (модификация Крона и Пашкеева)
6	32	147,129	154,646	0,377	154,675	0,296
8	32	110,485	110,441	0,109	110,445	0,191
12	32	73,844	80,957	0,281	80,946	0,486

В соответствии с данными табл. 1 и 2 можно рассчитать отклонение полученных значений критериев от оптимального значения при разном количестве устройств. Результаты расчётов приведены в табл. 3.

Таблица 3

Значения отклонений исследуемых критериев

п	Крона и СРМ	Крона и Пашкеева	Модификация Крона и СРМ	Модификация Крона и Пашкеева
6	8,072	8,102	7,517	7,546
8	0,042	0,033	0,044	0,04
12	7,502	7,579	7,113	7,102

Для большей наглядности значения, приведённые в табл. 3, представим в виде графика (рис. 4).

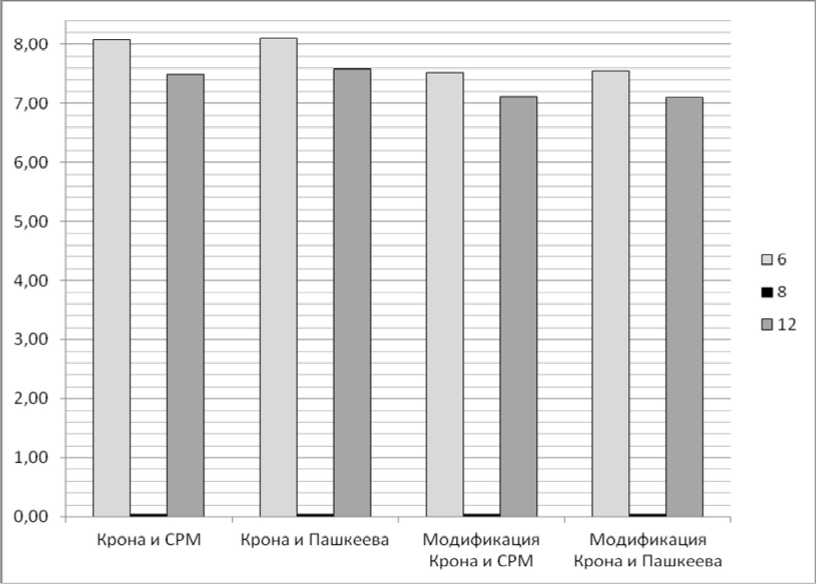
Рис. 4. Значения отклонений исследуемых критериев

Выводы. Оценивая полученные результаты, можно сделать вывод об эффективности описанных модификаций.

Сравнивались модификации классического и преобразованного алгоритма Крона, полученные с помощью алгоритма СРМ и алгоритма Пашкеева. По данным, приведённым в табл. 1 и 2, видно, что в первом случае результаты лучше. Однако при увеличении количества приборов более эффективна вторая пара модифицированных алгоритмов.

В целом, следует отметить, что модификации преобразованного алгоритма Крона дают лучшие результаты по сравнению с модификациями классического алгоритма, и это отчётливо видно на графике (рис. 4).

Список литературы Исследование алгоритма Крона и его модификации при различных исходных данных

Кофман, Э. Г. Теория расписаний и вычислительные машины/Э. Г. Кофман. -Москва: Наука, 1987. -334 с.
Кобак, В. Г. Сравнительный анализ алгоритмов решения задачи планирования в однородных вычислительных системах/В. Г. Кобак, М. С. Иванов//Математические методы в технике и технологиях -ММТТ-20: сб. тp. XX Междунар. науч. конф. -Ярославль, 2007. -Т. 2, секц. 2. -С. 56-57.
Кобак, В. Г. Повышение эффективности алгоритма Крона за счёт модификации начального распределения заданий/В. Г. Кобак, О. А. Золотых, Д. В. Титов//Современные проблемы информатизации в моделировании и социальных технологиях: сб. тр. XVI Междунар. открытой науч. конф. -Воронеж: Научная книга, 2011. -С. 246-251.

Статья научная