Исследование анизотропии пластических свойств монокристалла

One of most challenges of modern mechanics of continuous environments is construction of the general laws of evolution of a microstructure of a material in processes of plastic deformation. There are a lot of extensive experimental data and the general representations about how the metal microstructure changes are made. These experiments show sensitivity of processes of irreversible deformation to updating meso- and microstructures of a material which can change essentially in the course of deformation. The given work is devoted studying of systems of sliding activation features and dislocation pattern evolution of monocrystal at a various direction of an axis of the enclosed pressure.

Одной из наиболее сложных проблем современной механики деформируемого твердого тела является построение общих законов эволюции микроструктуры материала в процессах пластической деформации поликристаллических материалов. К настоящему времени накоплены обширные экспериментальные сведения и составлены общие представления о том, каким образом изменяется строение тела на уровне кристаллической решетки. Эти эксперименты свидетельствуют о значительной чувствительности процессов необратимого деформирования к модификации мезо- и микроструктуры материала, которая может существенным образом измениться в процессе деформирования. Данная работа посвящена изучению (с использованием методов дислокационной динамики ) особенностей активации систем скольжения и эволюции дислокационной структуры монокристалла меди при различных ориентациях по отношению к кристаллической решетке оси приложенного растягивающего напряжения.

Медь имеет гранецентрированную кубическую решетку (ГЦК). Для данного типа кристаллической решетки можно выделить три оси 4-го порядка W 1 , W 2 , W 3 (рис. 1), которые проходят через центры противоположных граней, четыре оси 3-го порядка ( A, B, C, D ), являющиеся пространственными диагоналями куба, и шесть осей 2-го порядка (I,II,III,IV,V,VI), проходящих через середины пар противоположных рёбер [5].

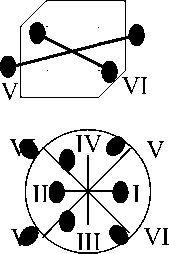
Рис. 1. Оси симметрии ГЦК-кристалла, их обозначения и стереографические проекции

Для монокристалла введем ортонормированный базис { e i | i= 1,2,3}, связанный с кристаллической решеткой и определяющий кристаллографическую систему координат х 1 х ₂ х ₃ (КСК). Для кристалла кубической симметрии вектор базиса e 1 совпадает с направлением [100], e 2 - [010] и e 3 - [001] (рис.2, а ).

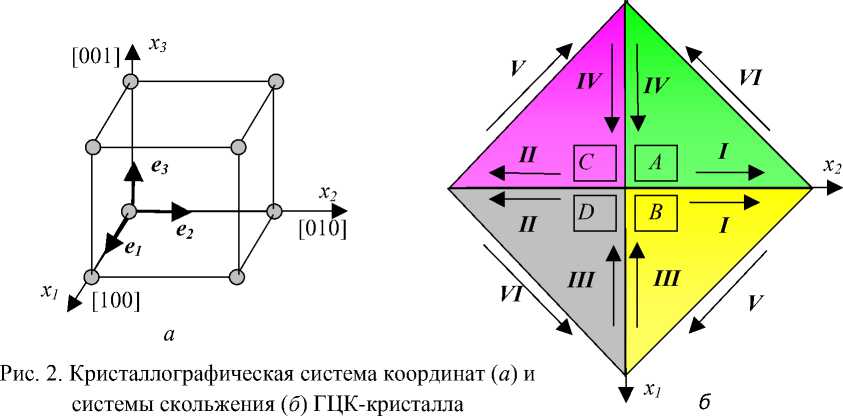
Дислокационное скольжение в ГЦК-кристалле осуществляется по плоскостям, нормали которых совпадают с осями 3-го порядка, и вдоль направлений в этих плоскостях, совпадающих с осями 2-го порядка. В каждой плоскости скольжения таких направлений три (рис. 2, б). Поэтому для ГЦК-кристалла имеем 12 систем скольжения (CC). Так как СС включает плоскость и направление скольжения, то для ее обозначения удобно использовать соответствующие обозначения осей симметрии кристалла. В табл. 1 приведены значения компонентов (в базисе КСК) единичного вектора нормали п к плоскости скольжения и вектора Бюргерса b направления скольжения всех 12 СС.

Таблица 1

Компоненты единичного вектора нормали к плоскости скольжения и вектора Бюргерса

СС

n 1

n 2

n 3

b 1

b 2

b 3

СС

n 1

n 2

n 3

b 1

b 2

b 3

AIV

- k n

k n

k n

k b

0

k b

CV

- к п

- к п

k n

- к ь

k b

0

AVI

- к ь

- к ь

0

CIV

k b

0

k b

AI

0

k b

- к ь

CII

0

- к ь

- к ь

BV

k n

k n

k n

k b

- к ь

0

DIII

k n

- к п

k n

- к ь

0

k b

BIII

- к ь

0

k b

DII

0

- к ь

- к ь

BI

0

k b

- к ь

DVI

k b

k b

0

Здесь к_п = 1/Vs , k b = 1/V2" .

Систему координат СС зададим тройкой ортогональных векторов bkn , где b -единичный вектор Бюргерса СС, п - единичная нормаль к плоскости скольжения CC, k - единичный вектор, лежащий в плоскости скольжения и ортогональный векторам b и п, и образующий с ними правую тройку векторов.

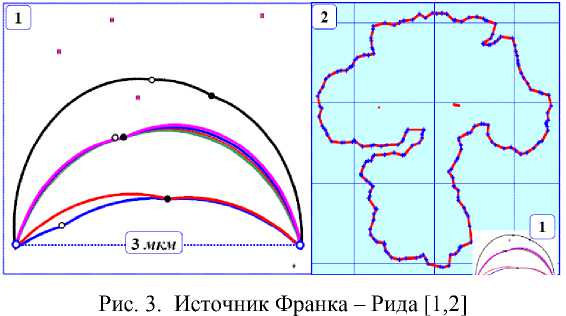
Концепции дислокационной динамики первоначально были разработаны Л.П. Кубиным [7] для двумерного случая прямых краевых дислокаций и позднее были обобщены для трехмерного случая. Основной идеей данного подхода является представление пластической деформации как следствия движения дислокаций по системам скольжения кристалла. При этом сами дислокации разбиваются на большое количество прямолинейных или дугообразных сегментов (рис. 3). В случае дуги окружности радиус сегмента зависит от напряжения, действующего на дислокацию.

В общем случае вектор Бюргерса каждого сегмента дислокации представляется суммой краевой и винтовой составляющей:

b = b кр + b вин .                                     (1)

Являясь линейным дефектом кристаллической решетки, сегмент дислокации инициирует поле напряжений [6], представленное в системе координат СС в табл. 2.

Таблица 2

Поле напряжений, вызванное сегментом дислокации

Краевая составляющая сегмента

° bb = - K G

³ x b + x k

2 ^, ( xb + 4 )

о -к X —_ xk

° kk = K G x k /       \2 ,

( x b + x k )

• ° nn = ^v( У ьь + У кк )

° bk

= K G x b

x_b - x_k

⁽ x b

+ x 2 )

° bn = ° kn = 0,

K g =

Gb

2n(1 - v)

Винтовая составляющая сегмента

Gbx

° nb = - -> / 2

^{2n ( x}b + x k )

_ _ Gbx

•°nk = n / 2

^{2n (} x b + x k )

° bb = ° kk = ° bk = ° nn = 0.

Здесь G - модуль сдвига, b - модуль вектора Бюргерса, v - коэффициент Пуассона.

Сегменты дислокации взаимодействуют дальнодействующими полями. При этом область действия упругого поля дислокации ограничена некоторой окрестностью этой дислокации. Усилия, действующие на сегмент дислокации, определяются суммированием воздействий со стороны остальных дислокаций с приложенной внешней нагрузкой,

MN т=т вн+ЕЕт у                            (5)

i = 1 j = 1

где т_вн - сдвиговое напряжение от приложенных внешних напряжений, T ij - касательное напряжение от j- го сегмента i -й дислокации. При этом учитываются объекты, создающие напряжения, превышающие заданное пороговое значение 5, то есть находящиеся в окрестности дальнодействия самой дислокации.

Зная действующее на сегмент касательное напряжения можно определить скорость смещения сегмента. В первом приближении можно использовать следующее соотношение:

v =

^T b

B ^,

где т - касательное напряжение, рассчитанное по соотношению (5), B - постоянная, характеризующая вязкое сопротивление (drag constant)

Движение дислокации возможно в том случае, если суммарное касательное напряжение, действующее на дислокацию со стороны других объектов, превышает пороговое значение барьера Пайерса.

Движение решеточных дислокаций и дислокационные реакции описываются единым набором локальных правил. При этом дислокационные реакции должны удовлетворять соотношению:

b l + b 2 = b 3 , b 12 + b 2 >  b ₃².

В результате дислокационных реакций могут образовываться новые решеточные дислокации (если реагируют нерасщепленные дислокации) или барьеры (если в реакцию вступают расщепленные дислокации). Новые дислокации могут появляться в результате работы источников Франка – Рида.

Следует заметить, что из-за наличия дальнодействующих упругих полей напряжений дислокаций при моделировании пластического деформирования методами дислокационной динамики «затраты» вычислительных ресурсов на каждой итерации пропорциональны квадрату количества взаимодействующих элементов. Таким образом, моделирование даже сравнительно небольших трехмерных объемов становится достаточно ресурсоемкой задачей. Тем не менее дислокационная динамика в последние годы получила широкое применение в различных моделях (часто – в моделях, охватывающих сразу несколько масштабных уровней). Существует свободно распространяемое программное обеспечение, реализующее основные концепции дислокационной динамики. В данной работе использована свободно распространяемая библиотека «microMegas» (Laboratoire d'Etude des Microstructure) [].

Исследовался объем монокристалла меди с размерами: 4,42487 x 4,89270 x x 5,86734 микрон. Были использованы параметры меди: G = 42 ГПа, v = 0,347, b = 0,256 нм, Т = 300 К , о₀ = 4,5 МПа, B = 5^10^-5 Па/c. Шаг по времени принимался равным 10^-9с. Начальное распределение дислокаций во всех экспериментах было одинаковое.

Было рассмотрено четыре варианта ориентации оси растяжения по отношению к КСК: {001}, {011}, {123}, {124}. Первые два варианта ориентации оси соответствуют так называемой «твердой» ориентировке (направление оси растяжения лежит вблизи или на границах стереографического треугольника, рис. 4), оставшиеся – «мягкой» (направление оси растяжения располагается в центре треугольника).

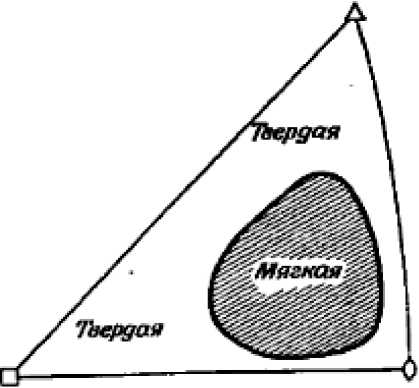
Рис. 4. Область «мягкой» и «твердой» ориентировок на стереографическом треугольнике [5]

Ниже приведены полученные σ-ε зависимости:

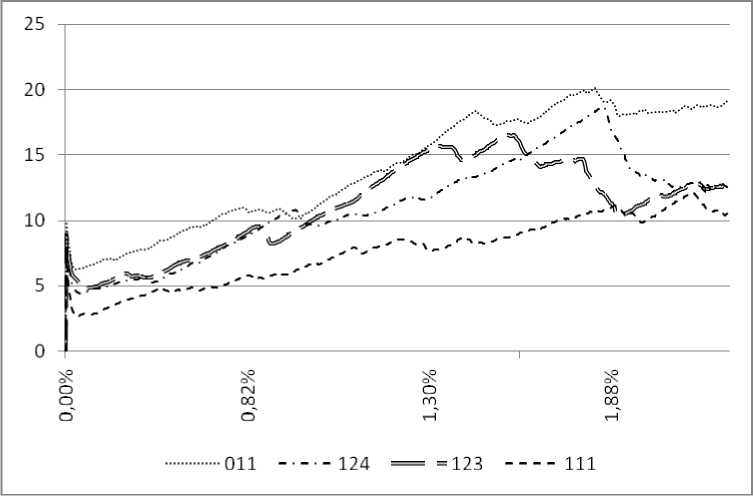
Рис. 5. Зависимость интенсивности напряжений (ГПа) от степени деформации (%) для различных направлений растяжения

Анализируя полученные результаты, можно заметить, что во всех случаях наблюдается так называемый «зуб» на начальной стадии деформации. Кроме того, в случае «мягкой» ориентации ({123}, {124}) после 0,018 % наблюдается спад напряжения.

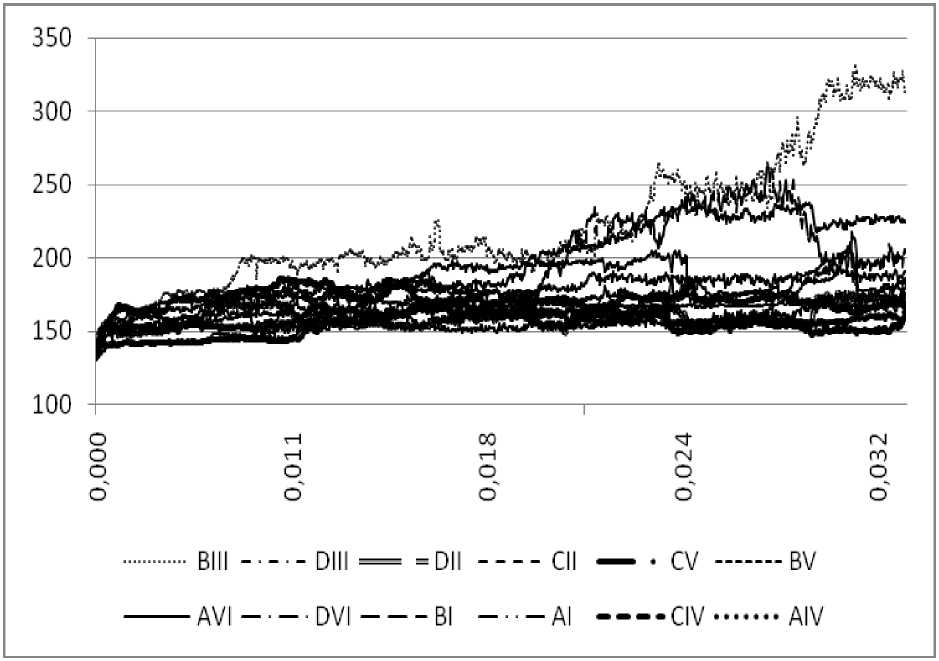
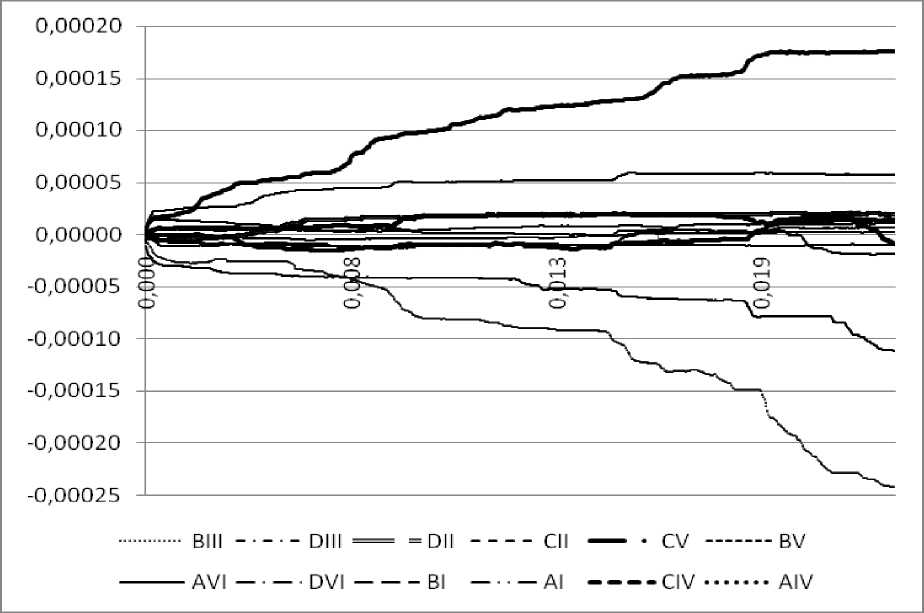
Были получены зависимости плотности дислокаций (109 см-2) и сдвигов по различным системам скольжений от пластической деформации (рис.6–9).

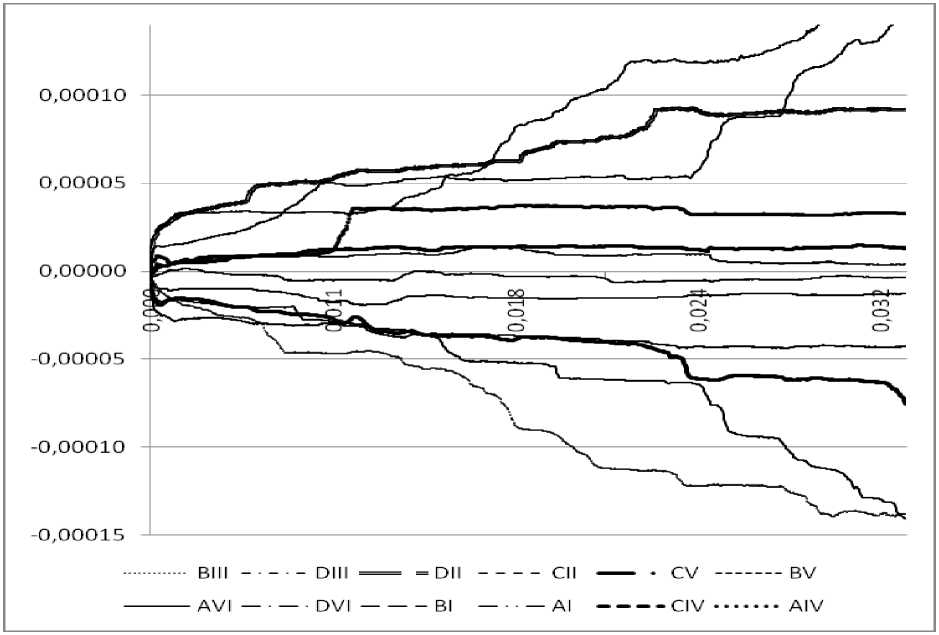
а

б

Рис.6. Зависимости плотности дислокаций ( а ) и сдвигов ( б ) по системам скольжения от пластической деформации (нагружение по {001})

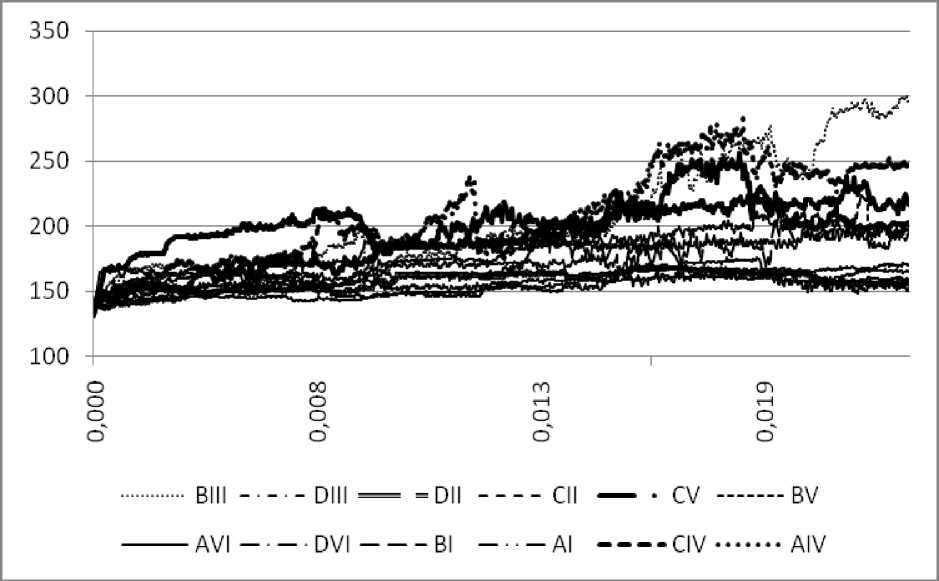
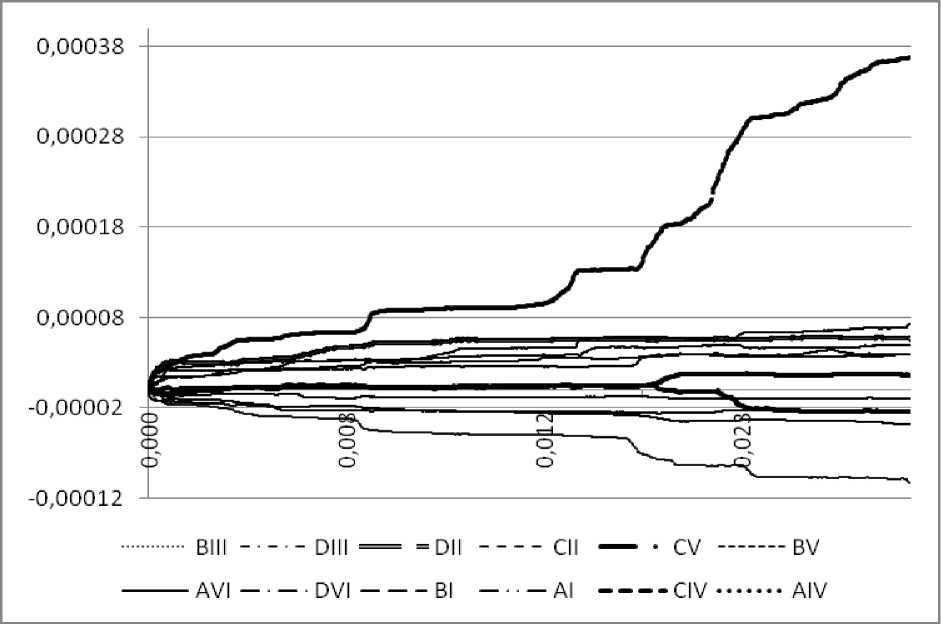
б

Рис.7. Зависимости плотности дислокаций ( а ) и сдвигов ( б ) по системам скольжения от пластической деформации (нагружение по {011})

а

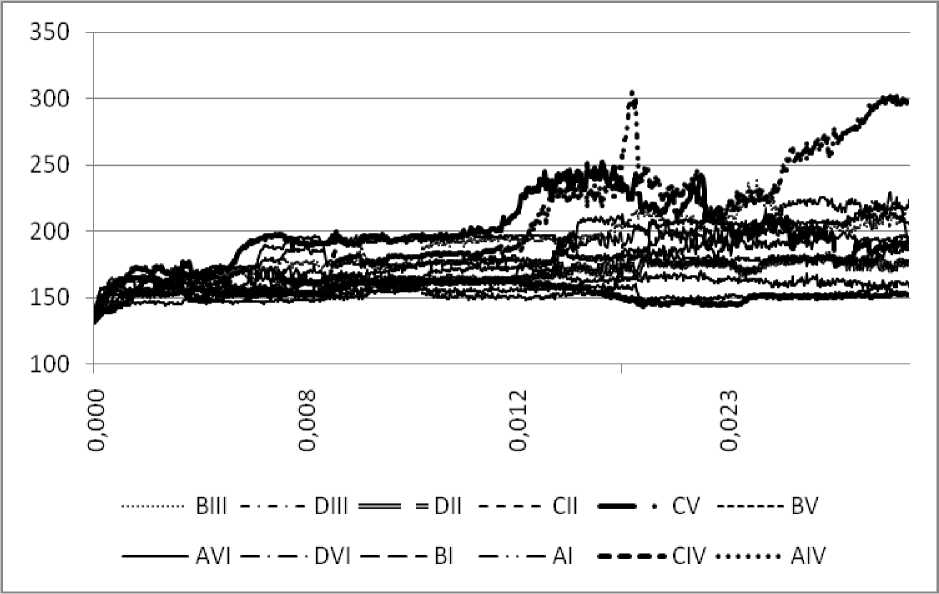
Рис.8. Зависимости плотности дислокаций ( а ) и сдвигов ( б ) по системам скольжения от пластической деформации (нагружение по {123})

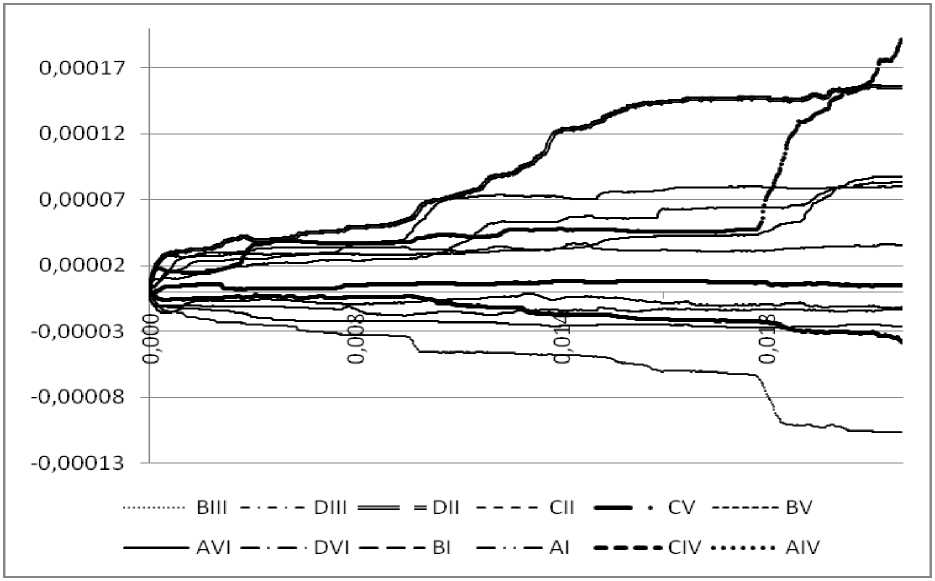
а

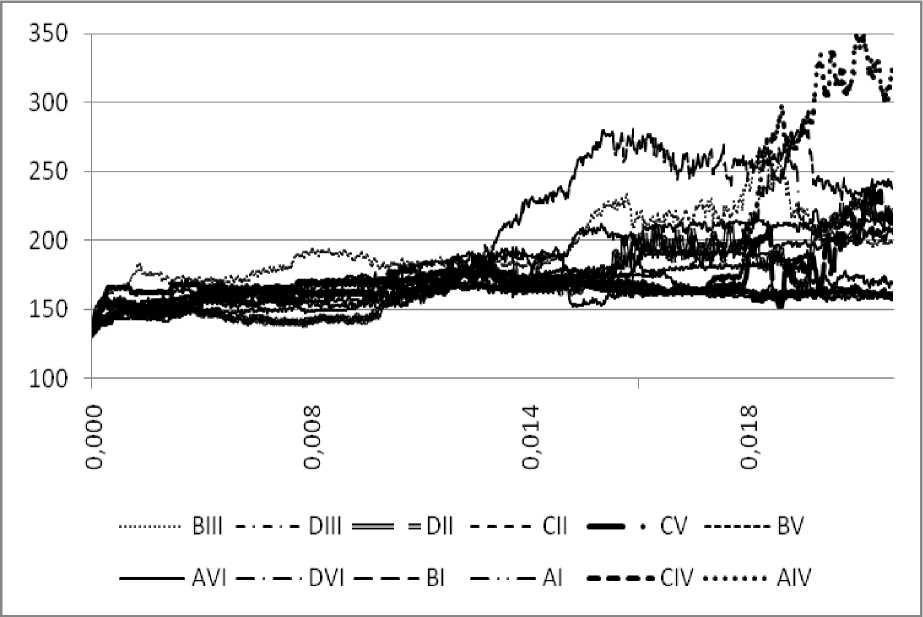
б

Рис.9. Зависимости плотности дислокаций ( а ) и сдвигов ( б ) по системам скольжения от пластической деформации (нагружение по {124})

Из полученных результатов можно сделать следующие выводы:

как и ожидалось, в случае твердой ориентации в кристалле наблюдается от шести до восьми активных систем скольжения. Для ориентации {123} отчетливо видна наиболее активная система скольжения. Ориентация {124} по активности систем скольжения больше похоже на твердую, так как зависимость сдвигов от пластической деформации свидетельствует о наличии пяти активных систем скольжения.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 07-08-96025-р_урал_а).