Исследование аппроксимативных возможностей радиально-базисной сети с различными функциями активации

Задача аппроксимации [1] является актуальной математической задачей. Для моделирования различных процессов, в частности экономических или физических, необходимо иметь функциональную зависимость, описывающую исследуемый процесс. На практике, для получения такой зависимости необходимо решить задачу аппроксимации, позволяющую на основании имеющихся данных построить функцию, описывающую исследуемый процесс. Для решения задачи аппроксимации существует множество математических методов, однако их использование в каждом случае сугубо индивидуально и не всегда возможно. В данной статье рассматривается использование нейронных RBF-сетей для аппроксимации плотности распределения вероятности случайного процесса, которую можно представить в виде [2] (1):

л m

f (x ) = Ewk ' Фк (x ,«X, • ,«n ), (1) к=0

где w_k – веса, настраивающиеся в процессе обучения сети, ф_к - функция активации нейронов, а 1 ..., a n - параметры функции активации.

активации нейронов радиально-базисные функции. Общий вид радиально-базисной функции можно описать уравнением:

Ф _к ( x ) = e ' x ^{k -} c ^{k )2}^ ^a k^k ,

Чаще всего в качестве функции активации нейронов радиально базисной сети используется функция Гаусса (2). В данной статье в качестве функции активации помимо функции Гаусса выбраны две ядерные функции [3]: квадратичная ядерная функция (3) и ядро Епанечникова (4).

¹⁵ • (1

x - c ) 2

2 ^²

0,75 • (1 - ) . (4) 2 a

В исследовании в качестве случайного процесса использовался набор выборок случайных величин с заданным законом распределения. Выборки генерировались при помощи метода обратной функции. В качестве входных данных для нейронной сети использовались значения высот столбцов гистограммы.

В качестве алгоритмов обучения был использован метод обратного распространения ошибки [4], а также алгоритм K-means [5]. Данный алгоритм относится к классу градиентных алгоритмов, т.е. изменения весов связей производятся в направлении минимизации градиента ошибки. Ошибка при обучении равна разности сигнала на выходе сети и эталонного значения выхода, соответствующего входным данным.

Обучение по алгоритму K-means заключается в размещении центров радиально базисных функций только в тех точках пространства, где имеются информативные данные, и нахождении таких значений коэффициента сигма, чтобы области охвата всех радиальных функций покрывали все пространство входных данных, причем любые две зоны могут перекрываться лишь в незначительной степени.

Критерием остановки обучения является достижение заданной погрешности. Результаты аппроксимации можно оценить по формуле:

a =

I 1 n                     ¹

У(у.-Уф.), n . =1

где y_i – значение функции, полученное сетью, y_фi – эталонное значение функции.

Для решения поставленных задач было разработано программное обеспечение, моделирующее работу нейронной сети. Внешний вид программы представлен на рис. 1.

В исследовании использовались различные законы распределения случайной величины, ниже рассмотрены результаты для нормального, равномерного закона и закона Симпсона. На рисунках представлено сравнение выходного сигнала сети с эталонным значением.

Закон распределения: закон Симпсона. Параметры: a=1, b=4. Количество нейронов скрытого слоя: 10. Метод обучения: метод обратного распро- странения ошибки. Коэффициент обучения: 0,2.

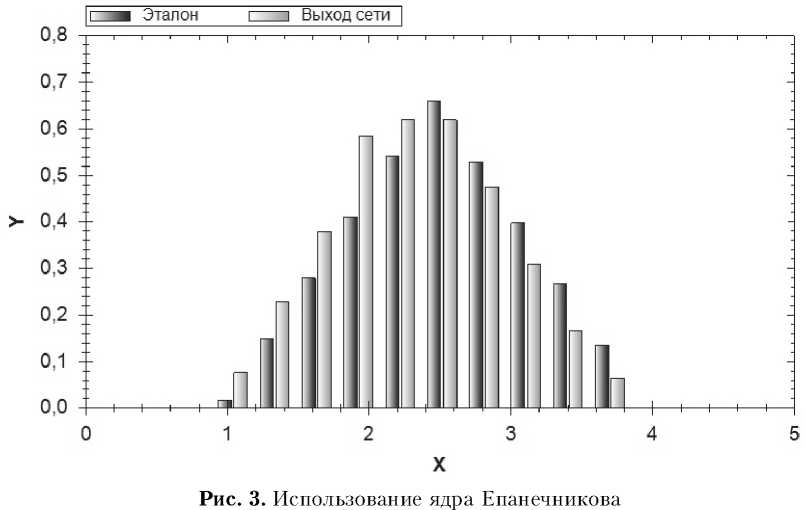
В табл.1 представлены значения среднеквадратического отклонения выходного сигнала сети от эталонного значения для каждого исследования. Значение слева от черты соответствует метода обратного распространения ошибки, значение справа – алгоритму K-means. Число нейронов скрытого слоя в эксперименте равно десяти. Анализируя таблицу, можно отметить, что выбор функции Гаусса в качестве функции активации сети является целесообразным для нормального закона распределения и закона Симпсона. Для равномерного закона распределения лучшим выбором будут ядерные функции.

В таблице 2 представлена зависимость значения среднеквадратического отклонения от числа нейронов скрытого слоя для случайной величины, распределенной по закону Симпсона. Значение слева от черты соответствует методу обратного распространения ошибки, значение справа – алгоритму K-means.

Как видно из таблицы, вариация числа нейронов в скрытом слое не оказывает серьезное влияние на аппроксимативные возможности сети. Из таблицы следует, что для определения функциональной зависимости оптимально выбрать пять-десять нейронов в скрытом слое.

В табл. 3 представлена зависимость значения

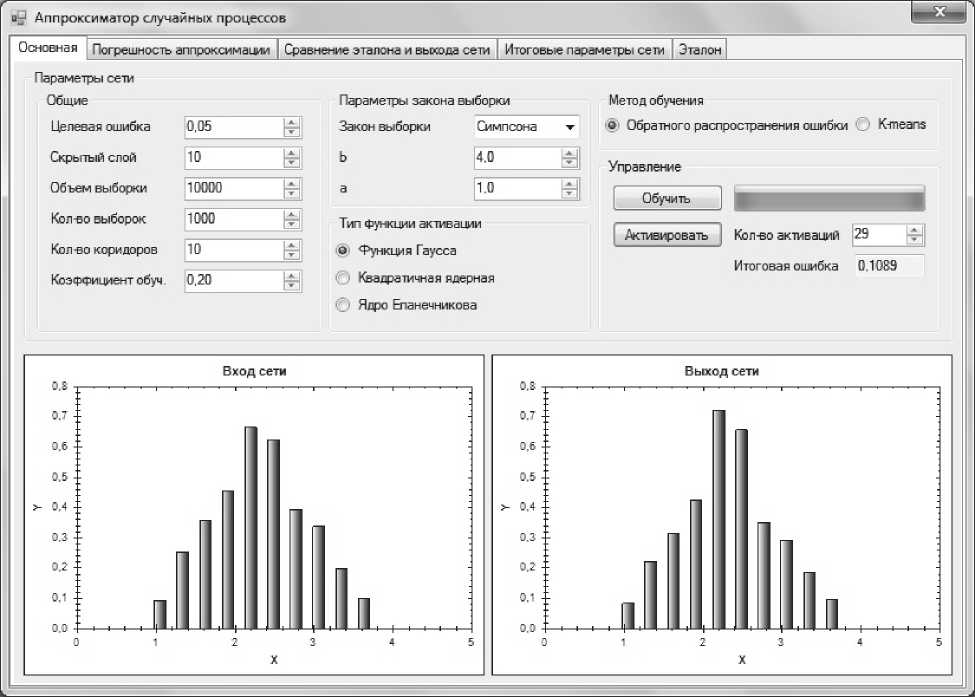
Рис. 1. Интерфейс программы

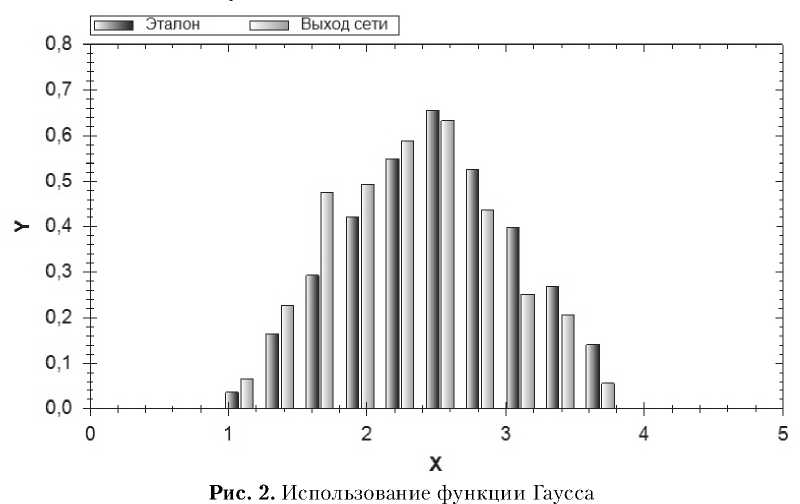
Таблица 1. Значения СКО для различных законов распределения.

	Нормальный	Равномерный	Сим псона
Функция Гаусса	0,024 / 0,013	0,005 / 0,003	0,033 / 0,005
Квадратичная ядерная	0,039 / 0,015	0,001 / 0,001	0,017 / 0,005
Ядро Епанечникова	0,027 / 0,015	0,001 / 0,001	0,018 / 0,007

среднеквадратического отклонения от коэффициента обучения. На практике от коэффициента обучения зависит сходимость алгоритма, слишком большой коэффициент может привести к нестабильности и расхождению. Анализ таблицы показывает, что при маленьком коэффициенте обучения алгоритм может не успеть сойтись при заданном числе шагов. Оптимальным значением коэффициента обучения является 0,2.

Исследования показали, что использование ядерных функций активации дает лучшие результаты для равномерного закона распределения и

Таблица 2. Значения СКО для различного числа нейронов скрытого слоя.

	5	10	20	30
Функция Гаусса	0,019 / 0,008	0,033 / 0,005	0,012 / 0,007	0,012 / 0,006
Квадратичная ядерная	0,039 / 0,007	0,017 / 0,005	0,011 / 0,004	0,016 / 0,004
Ядро Епанеч никова	0,014 / 0,007	0,018 / 0,007	0,098 / 0,004	0,012 / 0,003

Таблица 3. Значения СКО для различного коэффициента обучения

0,05 0,1 0,2 0,3 Функция Гаусса 0,024 / 0,007 0,015 / 0,007 0,033 / 0,005 0,054 / 0,006 Квадратичная ядерная 0,014 / 0,006 0,009 / 0,005 0,017 / 0,005 0,034 / 0,004 Ядро Епанечникова 0,022 / 0,009 0,012 / 0,006 0,018 / 0,007 0,013 / 0,006 закона Симпсона при обучении методом обратного распространения ошибки. Алгоритм K-means показывает идентичные результаты в обучении сети для различных функций активации, и в большинстве случаев дает лучшее значение СКО, чем метод обратного распространения ошибки. В общем случае, для получения наилучших результатов под конкретную задачу целесообразно подбирать оптимальную функцию активации.