Исследование асимптотики поля напряжений в окрестности вершины трещины в условиях ползучести с учетом поврежденности

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2024PNRPU MECHANICS BULLETIN

Точное прогнозирование поведения металлов и сплавов при ползучести при повышенной температуре важно для предотвращения катастрофических отказов систем, работающих в условиях длительного повышенного температурного воздействия. Такие условия эксплуатации приводят к накоплению повреждений при ползучести, которые, если их не контролировать, могут привести к неожиданному выходу из строя элемента конструкции или их совокупности. Более того, накопление повреждений при ползучести может значительно сократить срок службы системы и поставить под угрозу ее общую экономическую жизнеспособность. Таким образом, способность прогнозировать поведение конструкции при ползучести и накопление повреждений при ползучести в различных компонентах системы имеет технологическое значение для инженеров, желающих спроектировать и поддерживать систему, работающую в условиях повышенных температур. За прошедшие годы со времени пионерских работ Качанова и Работ-нова [1; 2] был разработан ряд эмпирических моделей для прогнозирования поведения различных металлов и сплавов с учетом повреждений при ползучести в реальных эксплуатационных условиях. Изначально Качанов [1] и Работнов [2] разработали определяющие уравнения, которые моделируют вторую и третью стадии ползучести и нелинейное механическое поведение материала при высоких температурах. Впоследствии уравнения Качанова – Работнова получили широкое распространение, и многочисленные исследования показали [3–14], что уравнения модели точно моделируют поведение при ползучести целого ряда металлов и сплавов. К настоящему времени предложены различные модификации и усовершенствования данной модели [3–14]. Одна из наиболее распространенных – модифицированная определяющая модель Качанова – Работнова – была предложена в [3] и обычно используется во многих исследованиях повреждений в режиме ползучести [4–6]. В [3] отмечается, что надлежащая процедура оценки предела прочности сварных соединений при ползучести должна позволять учитывать скорость деформации при ползучести, прочность и пластичность составляющих сварных соединений материалов. Следовательно, для этой цели могут быть использованы модели, учитывающие накопление повреждений. Общепринятым способом описания третьей стадии ползучести является использование уравнений Качанова – Работнова, в которых критическое значение поврежденности полагается равным единице при разрушении материала. Как известно [3], основной формой повреждения при ползучести в большинстве низколегированных ферритных сталей является кавитация. Однако многие примеры отказов оборудования [3] показали, что кавитированная область обычно занимает лишь малую часть всего сечения детали, и соответствующая деформация очень сильно локализована. Экспериментальные измерения в терминах модулей упругости могут привести к крити- ческим повреждениям, значительно меньшим единицы. Эти данные могут привести к неконсервативной оценке срока службы при ползучести с использованием обычных уравнений модели Качанова – Работнова [3]. На самом деле локализация повреждений является универсальной характеристикой материалов. Например, при одноосном растяжении поле напряжений является однородным, в то время как локализация повреждений и деформаций обнаруживается в определенных сечениях образца. В случае ползучести это означает, что в целом материал может находиться на второй стадии ползучести, в то время как определенные слабые места были на третьей стадии ползучести. Таким образом, в отношении эксплуатационных материалов было бы разумно считать, что некоторые области материала повреждены, в то время как некоторые не повреждены. Данное наблюдение привело авторов к модифицированной модели Качанова – Работнова [3].

В [4] подчеркивается, что ползучесть является существенным фактором, приводящим к выходу из строя паропроводов с высокой температурой и высоким давлением в периоды длительной эксплуатации. В [4] испытания на ползучесть были проведены при рабочей температуре 520 °C для труб из материала 1,25Cr– 0,5Mo, а константы ползучести и разрушения были получены путем подгонки данных испытаний на ползучесть. На основе модифицированного определяющего уравнения Качанова – Работнова в [4] составлена пользовательская подпрограмма, вычисляющая повреждения элемента трубы. В режиме ползучести прогнозирование повреждений проводилось методом конечных элементов с использованием кодов ABAQUS для паропроводов с высокой температурой и высоким давлением, которые обслуживались на нефтехимическом заводе. В [4] были получены распределение повреждений и местоположение максимального повреждения трубопроводов, о чем свидетельствуют результаты металлографического исследования. Более того, был также проведен анализ локальных повреждений при ползучести конической трубы, обслуживаемой в течение 100 000 ч, поскольку конические трубы, используемые в главном паропроводе, являются одним из наиболее уязвимых участков трубопроводов. Численный эксперимент, проведенный авторами [4], позволил получить данные о распределении повреждений и их эволюции в анализируемой конической трубе. Было определено место с максимальным значением поврежденности, которое совпадает с положением трещины в реальной испытанной трубе конической формы.

В [5] кратко изложены последние на тот период времени исследования по поведению сварных конструкций при высоких температурах. Предложен метод измерения локальной деформации, который позволяет непосредственно измерять свойства ползучести компонентов сварного шва. Представлены подходы континуальной механики поврежденности для изучения сокращения срока службы из-за наличия сварного шва и эф- фектов, связанных с ремонтом сварного шва. На основании модифицированных уравнений Качанова – Ра-ботнова изучается высокотемпературный рост трещины в условиях ползучести в сварных соединениях. Установлено, что несоответствия материалов в сварном соединении могут оказывать значительное влияние на развитие повреждений и рост трещины. В результате анализа были получены некоторые конструктивные соображения и изменения в действующих кодах.

Достаточно полные обзоры математических моделей, связывающих процессы накопления повреждений и эволюции полей напряжений и деформаций, обобщающих уравнения Качанова – Работнова, могут быть найдены в [13–15].

Поскольку после должного математического и экспериментального обоснования теоретических моделей континуальной теории поврежденности [6; 12–16] стало очевидно, что дальнейшее развитие механики повреждений неотъемлемо связано с внедрением математических моделей в расчетную схему метода конечных элементов, то с середины 90-х гг. прошлого века различные эволюционные уравнения были инкорпорированы в численную процедуру метода конечных элементов. Например, в [6] на основе модифицированного определяющего уравнения модели Качанова – Работнова составлена пользовательская подпрограмма для материалов (UMAT) для расчета повреждений при ползучести труб с внедренными сферическими дефектами. Параметрические коэффициенты, введенные в модель, охватывают девять местоположений дефектов, пять коэффициентов глубины дефекта и ряд других геометрических параметров. В [16] сообщается о моделировании роста трещин в условиях ползучести в сварных соединениях сосудов при высокой температуре с использованием модифицированной модели континуальной механики повреждений с учетом пластических деформаций, которая основана на континуальной модели Качанова – Работнова и использует концепцию исчерпания пластичности. Предлагаемая модель обладает ключевым преимуществом перед существующими моделями в том, что для определения и калибровки требуется меньшее количество материальных констант. Новая модифицированная модель была внедрена в определяемую пользователем подпрограмму в ABAQUS, а затем использована для прогнозирования роста трещин при ползучести в сварных соединениях сосудов марки 91. На основании проведенных вычислений показано, что возникновение и рост трещин при ползучести в сосудах произойдет в зонах термического воздействия сварных соединений, связанных с торцевыми заглушками, что хорошо согласуется с результатами соответствующих испытаний сосудов. Более того, прогнозируемый срок службы деталей с выточками и емкостей при ползучести с использованием предложенной модели достаточно хорошо коррелировал с экспериментальными результатами. Это свидетельствует, что модифицированная модель поврежденности, дополнительно учитывающая пластические деформации, может быть с уверенностью использована для прогнозирования роста трещин в режиме ползучести и срока службы высокотемпературных конструкций. В [6] отмечается, что модели, основанные на континуальной механике поврежденности, широко используются для прогнозирования повреждений при ползучести и срока службы в условиях ползучести. Как правило, эти методы позволяют охарактеризовать все стадии ползучести и могут быть легко внедрены в программу конечных элементов для прогнозирования деформации ползучести и поведения сталей при повреждениях при высоких температурах. В [17] реализован широкий конечно-элементный расчет с использованием кода конечных элементов ANSYS для изучения влияния повреждений на поля напряжений у фронта трещины для компактного образца. Для численного определения полей напряжений и скоростей деформаций в [16] сначала находится скорость накопления поврежденности путем подстановки напряжений, полученных на начальной итерации, в кинетическое уравнение модели Качанова – Работнова. После определения поврежден-ности с помощью численного интегрирования и подстановки скорости деформации ползучести в определяющее уравнение из результирующей функции повре-жденности, введенной в ANSYS, вычисляются поля напряжения, поврежденности и скорости деформации. Наконец, после получения решения нелинейной задачи выходной файл ANSYS используется в качестве входных данных для специального кода, разработанного для определения безразмерных угловых распределений напряжений–деформаций, величины поврежденности и коэффициента интенсивности напряжений в режиме ползучести.

В [18] было проведено определение предельного состояния алюминиевого сплава при сложном напряженном состоянии. Целью исследования является определение влияния накопленных повреждений в материале, находящемся в сложном напряженном состоянии, на характеристики несущей способности материала. Рассмотрены различные виды комбинированного нагружения растяжением, сжатием, кручением и внутренним давлением. Объектом численных и экспериментальных исследований является полый цилиндрический образец с окружной выточкой. В вычислительной части в качестве закона изотропного упрочнения использовалась экспоненциальная и степенная аппроксимирующие функции. Для определения параметра поврежденности был использован эволюционный закон накопления по-врежденности Леметра. Обобщенный закон накопления повреждений Леметра и закон изотропного упрочнения были интегрированы в конечно-элементный код ANSYS в виде динамически связанной библиотеки пользовательских материалов для трехмерных задач. Получены напряженно-деформированное состояние, поле повреждений, а также значения предельных напряжений при различных типах нагружения. Численно проведено сравнительное исследование различных теорий пре- дельного напряженного состояния с учетом накопления повреждений при сложном напряженном состоянии. В [19] описывается методология определения параметров и констант модели поврежденности типа Леметра на основе стали 25Cr1Mo1V. Модель реализует законы изотропного упрочнения и кинематического упрочнения Армстронга – Фредерика. Алгоритм определения констант и параметров основан на стандартных испытаниях на одноосное растяжение для описания изотропного упрочнения и малоцикловых испытаниях на усталость для определения констант модели поврежденно-сти и кинематических параметров упрочнения. На основе найденных констант и параметров методом конечных элементов было смоделировано циклическое нагружение цилиндрических образцов и получена кривая усталости для стали 25Cr1Mo1V. Было достигнуто хорошее соответствие между экспериментальной и прогнозируемой усталостной долговечностью.

Исследование [20] посвящено разработке модели для прогнозирования скорости роста усталостной трещины при ползучести на основе концепций зон разрушения. Предполагается, что скорость роста трещины может быть определена путем интегрирования уравнений скорости накопления повреждений в зону процесса разрушения независимо для малоцикловой усталости и ползучести. В случае малоциклового усталостного нагружения использовалась функция накопления повреждений, предложенная Йе и Вангом [21], а также классический степенной закон Качанова – Работнова для характеристики накопления повреждений при ползучести. Размер зоны процесса разрушения рассчитывается на основе концепции нелинейных коэффициентов интенсивности напряжений, предложенной В.Н. Шляннико-вым [22]. Приведены предпосылки для предложенной общей модели скорости роста трещин при взаимодействии ползучести и усталости для сравнения с экспериментальными данными. Экспериментальное исследование скорости роста трещин при взаимодействии ползучести и усталости проведено для компактного образца на растяжение, изготовленного из 20CrMoV5. Скорость роста трещин определялась при повышенной температуре 550°C в соответствии со стандартом ASTM E2760. Предсказания скорости роста трещин были сопоставлены с экспериментальными данными для стали 20CrMoV5, полученными при повышенной температуре, и совпадение было признано удовлетворительным.

В [23] предложена и разработана модификация модели повреждений Леметра, базирующаяся на внедрении в модель функции, чувствительной к параметру Лоде. Усовершенствованная модель интегрирована в программный пакет, реализующий метод конечных элементов в форме динамически подключаемой пользовательской библиотеки. Модель дает возможность учета изотропного упрочнения на основе экспоненциальной модели и модели кинематического упрочнения Армстронга – Фредерика. В работе [23] выполнен глубокий численный анализ методом конечных элементов и по- лучены диаграммы предельных состояний для трех типов экспериментальных образцов. Испытаны образцы на сжатие при дополнительном внешнем давлении, образцы с кольцевой выточкой при одноосном растяжении и полые образцы при совместном действии растяжения, кручения и внутреннего давления. Сформулированы рекомендации для выбора параметров модели для прогнозирования предельных состояний при многоосном нагружении.

В настоящее время современные направления дальнейшего научного поиска связаны с возможностью использования машинного обучения и подходов искусственного интеллекта, а также с общим развитием технологии метода конечных элементов. Например, в [7] подчеркивается, что точное прогнозирование поведения сплавов при ползучести при повышенной температуре важно для предотвращения катастрофических отказов систем, работающих в условиях длительного повышенного температурного напряжения. В [7] объединена модель ползучести Качанова – Работнова с многоцелевым генетическим алгоритмом для прогнозирования поведения сплава 617 при высокой температуре и при различных напряженных состояниях. Показано, что оптимизированная модель ползучести Качанова – Ра-ботнова может отражать общее поведение сплава при повышенных температурах в широком диапазоне напряженных условий.

В [24] модель повреждений при ползучести Лю – Мураками усовершенствована для прогнозирования срока службы различных образцов с трещинами при ползучести. Модифицированный закон разрушения при ползучести реализован в рамках расширенного метода конечных элементов (XFEM) для выполнения моделирования роста трещины при ползучести с учетом пластических деформаций. Функция трехосности напряжений введена в модифицированную модель повреждения Лю – Мураками для учета изменения скорости роста трещин. Кроме того, предложено новое определение трехосности напряжений (отношение линейной комбинации максимального главного напряжения и гидростатического напряжения к интенсивности напряжений), основанное на критерии разрушения Леки и Хейхерста. Новое определение трехосности напряжений является ключевым параметром при прогнозировании времени до разрушения. Модифицированная модель повреждения при ползучести Лю – Мураками в [24] используется для моделирования роста трещин при ползучести нескольких образцов при различных условиях нагружения. Также проводятся параметрические исследования для изучения влияния различных параметров на рост трещин в условиях ползучести. Более того, комбинированная система уравнений континуальной механики поврежденности и XFEM используется для прогнозирования срока службы лопатки турбины с учетом возможного роста трещины при ползучести. В [24] установлено, что модифицированный кинетический закон накопления повреждений при ползучести Лю – Мураками точно предсказывает срок службы компонентов с трещинами при различных ограничительных условиях.

В настоящей работе реализована попытка включить каноническую модель Качанова – Работнова [1; 2] в расчетную схему метода конечных элементов и выявить асимптотическое поведение напряжений в условиях накопления повреждений.

Целью исследования является выявление асимптотики полей напряжений в окрестности вершины трещины в условиях ползучести с учетом накопления повре-жденности на основании конечно-элементного анализа напряженно-деформированного состояния у вершины трещины в МКЭ-комплексе SIMULIA Abaqus с использованием процедуры UMAT, позволяющей инкорпорировать процесс накопления повреждений в расчетную схему комплекса. Для выявления асимптотики в работе выполнено: 1) конечно-элементное моделирование нагружения пластины с центральной горизонтальной и наклонной трещиной в условиях установившейся ползучести; 2) включение с помощью написанной пользовательской процедуры UMAT в расчетную схему метода конечных элементов процесса накопления повреждений с течением времени в соответствии с классической моделью поврежденности Качанова – Работнова; 3) исследование поля напряжений в окрестности вершины трещины и получение асимптотики полей напряжений вблизи вершины трещины в пластине.

Фундаментальные уравнения

Работа посвящена исследованию асимптотики полей напряжений в окрестности вершины трещины в пластине в условиях ползучести с учетом накопления поврежден-ности в соответствии с моделью Качанова – Работнова. Для моделирования ползучести выбран степенной закон Бейли – Нортона, имеющий следующий вид:

_    /    \ n-1

•    3 sfC^   sij3

Sj = 7^1- I —, Ce =. s-sjS,

2 ^ v J V V 2

где c _e - интенсивность касательных напряжений, s ij -компоненты скорости деформации ползучести; c j -компоненты напряжений; s j = c j - (1/3) c _kk 5 j - компоненты девиатора напряжений, V - параметр сплошности Качанова, B , n – постоянные материала.

В соответствии с моделью Качанова – Работнова [1; 2] определяющие уравнения (1) дополняются степенным эволюционным уравнением

m

d V = AI Ce I dt I V J

,

где A , m – постоянные материала, определяемые экспериментально.

Расчетная процедура и численные результаты

В расчетном комплексе SIMULIA Abaqus была выполнена большая серия вычислительных экспериментов нагружений пластины (рис. 1), соответствующих нормальному отрыву и смешанному нагружению, в условиях ползучести без учета и с учетом процессов накопления повреждений в соответствии с моделью (1) и (2). Константы материала, выбранные на основании экспериментальных данных, приведенных в [15], представлены в табл. 1 и 2.

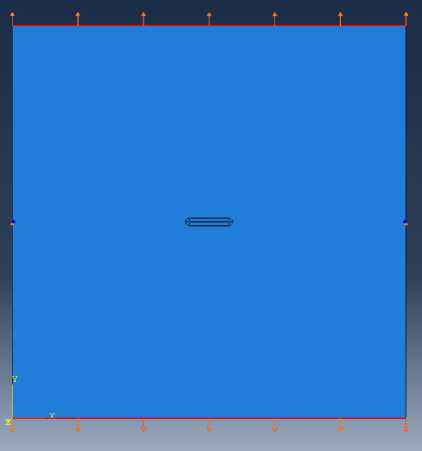
Рис. 1. Геометрия пластины и система приложенных нагрузок

Fig. 1. Schematic of the cracked plate and applied loads

Была выбрана пластина со следующими геометрическими размерами: длина стороны квадратной пластины составляла 100 мм, длина выреза равна 10 мм, радиус закругления равен 0,001 мм. На рис. 2 приведена типичная конечно-элементная сетка, окружающая трещину с закругленной вершиной.

Результаты расчета напряженно-деформированного состояния для пластины в условиях ползучести с использованием конституциональных соотношений, имеющихся в программном комплексе (классический закон Нортона теории установившейся ползучести), приведены на рис. 3, 4. На рис. 3 показаны распределения напряжений тензора напряжений у вершины трещины для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка).

После проведения расчетов на основе классического уравнения Нортона на языке программирования FORTRAN разработана программа, описывающая процесс накопления повреждений в условиях ползучести. Процедура внедрена в конечно-элементный код программного комплекса SIMULIA ABAQUS с использованием стандартной подпрограммы UMAT. Проведено моделирование нагружения пластины с центральной трещиной для различных значений констант материала. Константы материала приведены в табл. 2. Распределение напряжений с течением времени показано на рис. 5, где приведены распределения компонент тензора напряжений σ 11 , σ 12 , σ 22 у вершины трещины для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 часа (третья колонка) и 5000 ч (четвертая колонка) с учетом процессов накопления повреждений.

Таблица 1

Материальные константы, используемые в КЭ-расчете

Table 1

Material constants used in FEM computations

№ модели	Модуль Юнга E , H/mm2	Коэффициент Пуассона	B , (H/mm2)– n ч–1	n	Нагрузка P , H/mm2
1	210000	0,3	10 –10	2	20
2	210000	0,3	10 –12	3	20
3	210000	0,3	10 –15	4	20
4	210000	0,3	10 –16	5	20

Таблица 2

Материальные константы, используемые в КЭ-расчете с учетом поврежденности

Table 2

Material constants used in FEM computations taking into account the damage accumulation process

№ модели	Модуль Юнга E , H/mm2	Коэффициент Пуассона	B , (H/mm2)– n ч–1	n	A , (H/mm2)– n ч–1	m	Нагрузка P , H/mm2
1	210000	0,3	10 –13	3	0,1	2,5	10
2	210000	0,3	10 –16	4	0,1	2,8	10
3	210000	0,3	10 –19	5	0,1	3,5	10

Рис. 2. Типичная конечно-элементная сетка с закругленной вершиной

Fig. 2. A typical finite element grid with a blunted tip

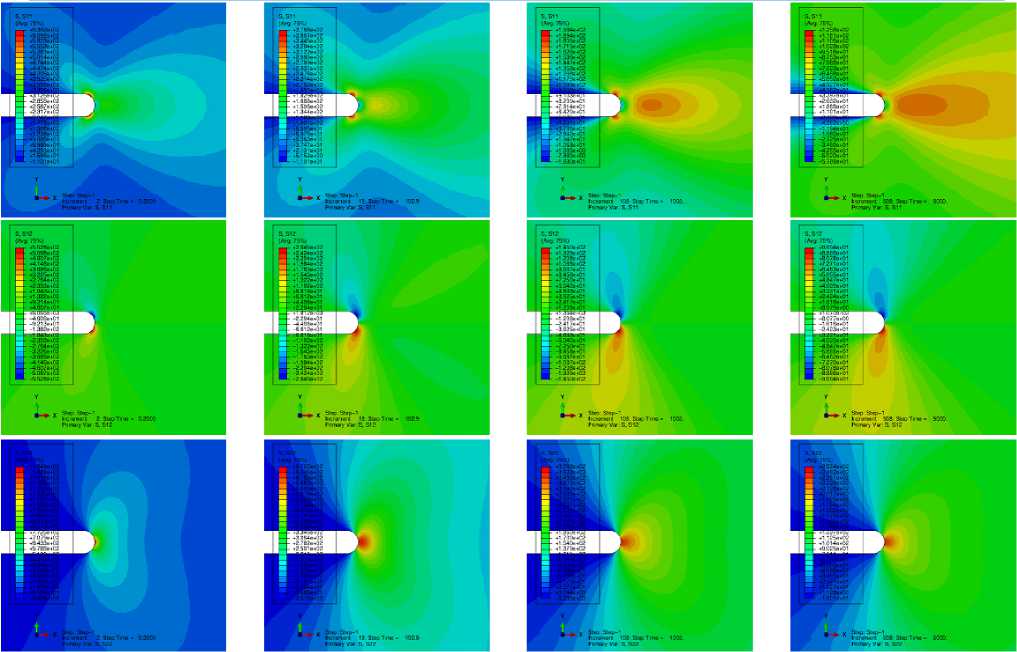
Рис. 3. Распределения компонент тензора напряжений σ 11 , σ 12 , σ 22 у вершины трещины в различные моменты времени: для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка)

Fig. 3. Distributions of the stress tensor components at different times: at 0.2 hours (first column), 102.9 hours (second column), 1003 hours (third column) and 5000 hours (fourth column)

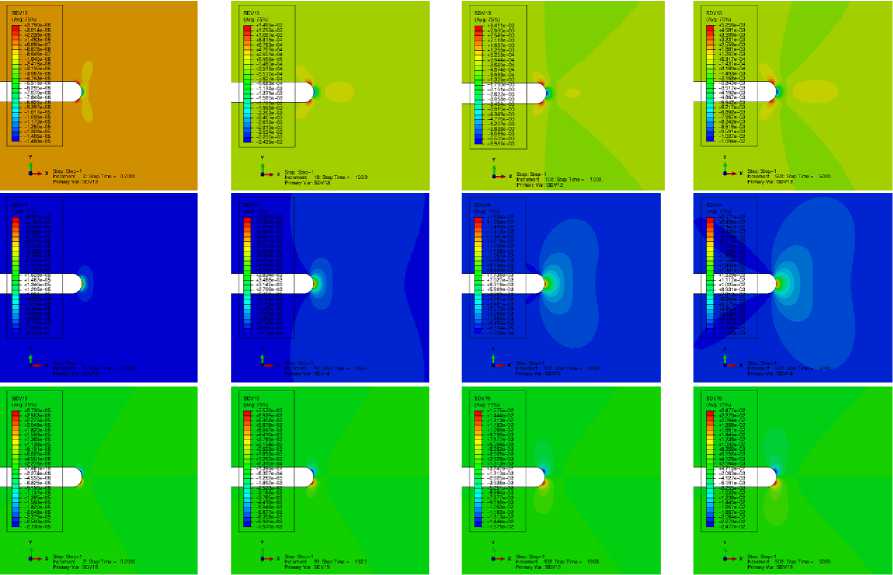
Рис. 4. Распределения компонент тензора деформаций ползучести ε 11 , ε 22 , ε 12 у вершины трещины в различные моменты времени: для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка)

Fig. 4. Distributions of the creep strain tensor components at different times: at 0.2 hours (first column), 102.9 hours (second column), 1003 hours (third column) and 5000 hours (fourth column)

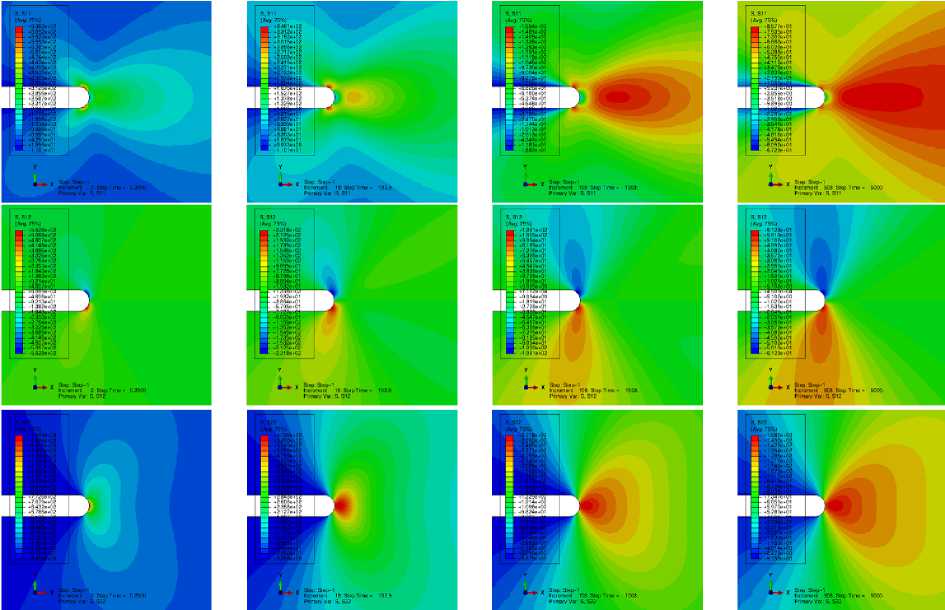
Рис. 5. Распределения компонент тензора напряжений σ 11 , σ 12 , σ 22 у вершины трещины для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка) с учетом процесса накопления повреждений

Fig. 5. Distributions of the stress tensor components at different time: at 0.2 hours (first column), 102.9 hours (second column), 1003 hours (third column) and 5000 hours (fourth column) with taking into account damage accumulation processes

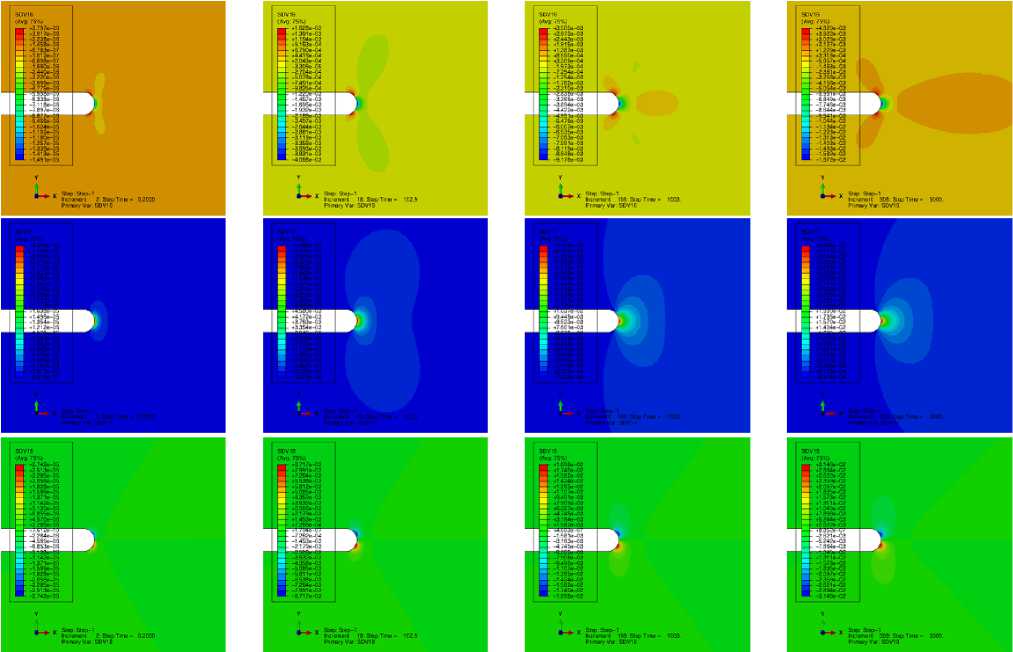
Рис. 6. Распределения компонент тензора деформаций ползучести ε 11 , ε 22 , ε 12 у вершины трещины в различные моменты времени: для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка) с учетом процессов накопления повреждений

Fig. 6. Distributions of the creep strain tensor components at different times: at 0.2 hours (first column), 102.9 hours (second column), 1003 hours (third column) and 5000 hours (fourth column) with taking account damage accumulation processes

На рис. 6 отображена эволюция деформаций ползучести ε 11 , ε 22 , ε 12 у вершины трещины с течением времени: для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка) с учетом процессов накопления повреждений. Из проведенного конечно-элементного анализа и сравнения приведенных графиков следует, что присутствие повреждений сказывается как деградация всех прочностных характеристик твердого тела, поэтому при прочих равных условиях все величины, инвариантно описывающие напряженное состояние, отличаются в сторону уменьшения от таковых для неповрежденного тела; для деформаций ситуация обратная: поврежден-ность сказывается как ускорение ползучести, а ускоренная ползучесть приводит к существенно большим деформациям ползучести.

На рис. 7 в одном графическом окне изображены распределения интенсивности напряжений в условиях ползучести без учета поврежденности и с учетом по-врежденности. Из рис. 7 отчетливо видно, что интенсивность напряжений в случае среды с поврежденно-стью существенно меньше, по сравнению с значениями интенсивности напряжений в эти же моменты времени для среды без поврежденности. Особый интерес вызывают область накопления повреждений, формирующаяся у вершины трещины, и ее развитие с те-

чением времени. На рис. 8 представлены распределения сплошности, полученные в соответствии с моделью Качанова – Работнова (1), (2) в различные моменты времени.

В рамках проведенного конечно-элементного вычислительного эксперимента для анализа смешанного нагружения рассмотрено растяжение пластин с наклонными под углами 45° и 60° к горизонтали разрезами в режиме ползучести с учетом процессов деградации сплошности. Эволюция области активного накопления повреждений у вершин трещин, составляющих углы 45° и 60° с горизонталью, продемонстрирована на рис. 9. Составляющие тензора деформаций, ассоциированные с вершиной наклонной под углом 45° к горизонтали трещиной, найденные с помощью разработанной процедуры UMAT для учета процессов деградации сплошности, приведены на рис. 10. На рис. 11 проиллюстрированы компоненты тензора деформаций, ассоциированные с вершиной, наклонной под углом 60° к горизонтали трещиной, найденные с помощью разработанной процедуры UMAT для учета процессов деградации сплошности. На рис. 12 показаны полученные распределения интенсивности касательных напряжений, ассоциированных с вершиной наклонной трещины: под углом 45° (верхний ряд) и под углом 60° (нижний ряд).

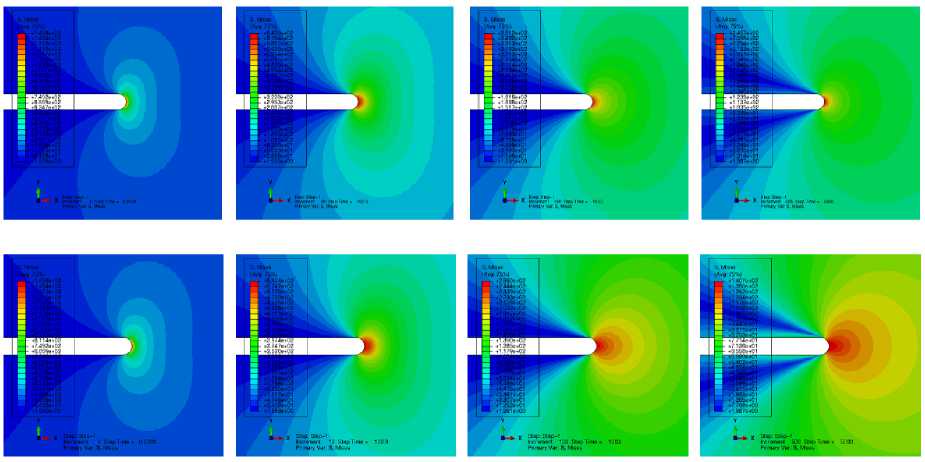
Рис. 7. Картины распределений интенсивности напряжений вблизи вершины трещины в условиях ползучести в различные моменты времени (первый ряд – без учета повреждений, второй ряд – с четом процессов накопления повреждений): для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка)

• Fig. 7.    Distributions of the von Mises stress at different times: at 0.2 hours (the first row corresponds to creep regime without damage accumulation whereas the second row corresponds to the creep regime with damage accumulation processes), 102.9 hours (second column), 1003 hours (third column) and 5000 hours (fourth column) with taking account damage accumulation processes

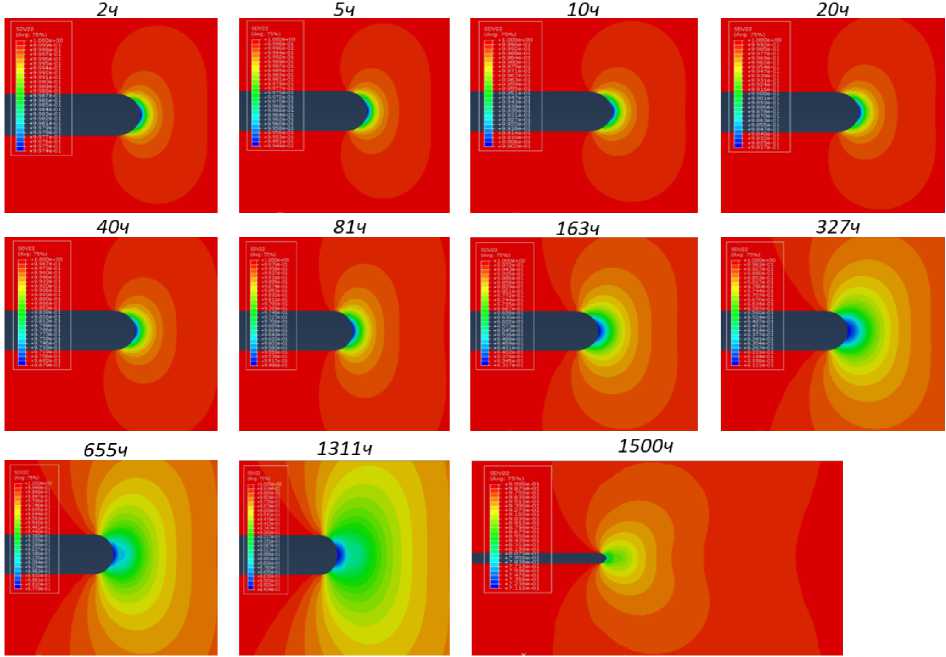
Рис. 8. Распределения параметра сплошности, полученные в соответствии с эволюционной моделью Качанова – Работнова, в разные моменты времени

• Fig. 8.    The distributions of the continuity parameter obtained in accordance with the Kachanov – Rabotnov evolutionary model

at different times

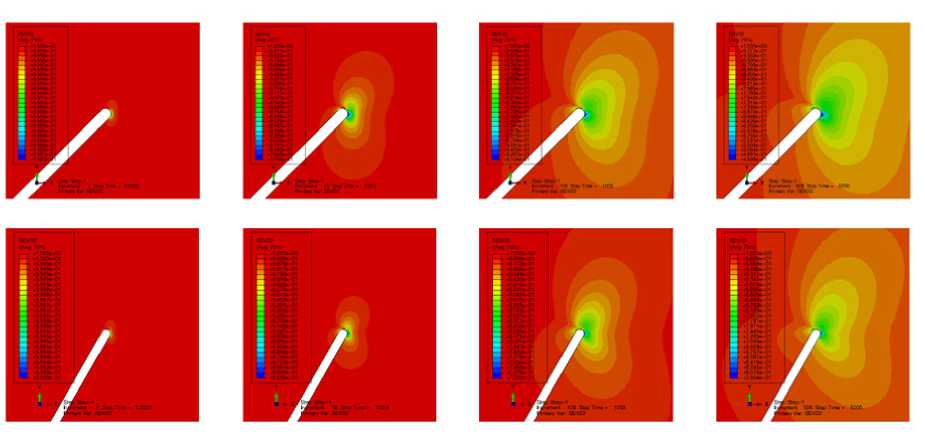
Рис. 9. Распределения параметра сплошности, полученные в соответствии с эволюционной моделью Качанова – Работнова, вблизи вершин наклонных под углами 45° и 60° трещин в разные моменты времени

Fig. 9. The distributions of the continuity parameter obtained in accordance with the Kachanov – Rabotnov evolutionary model in the vicinity of the inclined cracks at 45° и 60° at different times

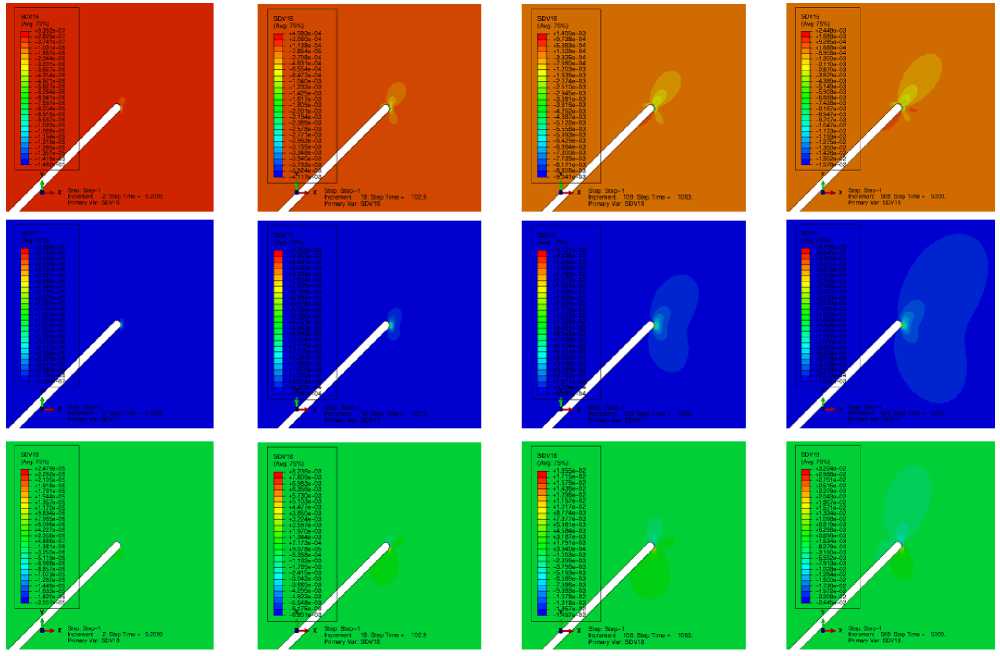
Рис. 10. Распределения компонент тензора деформаций ползучести ε 11 , ε 22 , ε 12 у вершины наклонной под углом 45° трещины для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка) с учетом процессов накопления повреждений

Fig. 10. Distributions of the creep strain tensor components ε 11 , ε 22 , ε 12 at different time: at 0.2 hours (first column), 102.9 hours (second column), 1003 hours (third column) and 5000 hours (fourth column) with taking account damage accumulation processes

Рис. 11. Распределения компонент тензора деформаций ползучести ε 11 , ε 22 , ε 12 у вершины наклонной под углом 60° трещины для 0,2 ч (первая колонка), 102,9 ч (вторая колонка), 1003 ч (третья колонка) и 5000 ч (четвертая колонка) с учетом процессов накопления повреждений

Fig. 11. Distributions of the creep strain tensor components ε 11 , ε 22 , ε 12 near the inclined crack tip at 60° at different time: at 0.2 hours (first column), 102.9 hours (second column), 1003 hours (third column) and 5000 hours (fourth column) with taking account damage accumulation processes

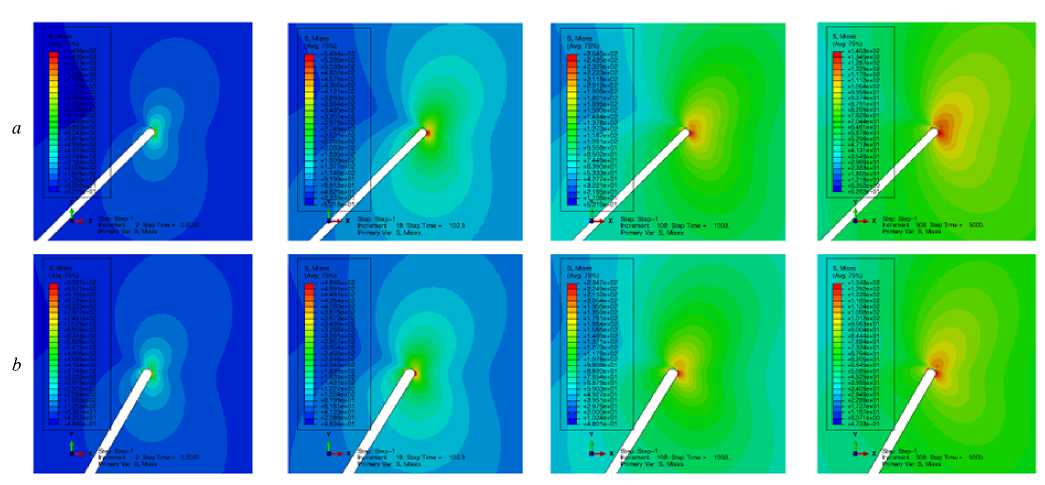
Рис. 12. Распределение интенсивности касательных напряжений, ассоциированных с вершиной наклонной трещины: под углом 45° (верхний ряд) и под углом 60° (нижний ряд)

Fig. 12. Distribution of the von Mises stress associated with the tip of an inclined crack: at an angle of 45 degrees (upper row) and at an angle of 60 degrees (lower row)

Анализ распределений механических полей, полученных с помощью конечно-элементного моделирования

Полученные в ходе конечно-элементного анализа поля напряжений, деформаций и сплошности позволяют построить угловые и радиальные распределения полей, ассоциированных с вершиной трещины. На рис. 13 приведены угловые распределения тензоров напряже- ний и деформаций, построенные вдоль линии продолжения трещины для случая наклонной трещины углом 45° к горизонтали на различных расстояниях от вершины трещины (на графиках указаны безразмерные расстояния, отнесенные к длине трещины). На рис. 14 проиллюстрированы угловые распределения тензоров напряжений и деформаций, построенные вдоль линии продолжения трещины для случая наклонной трещины углом 60° к горизонтали для различных расстояний от кончика трещины.

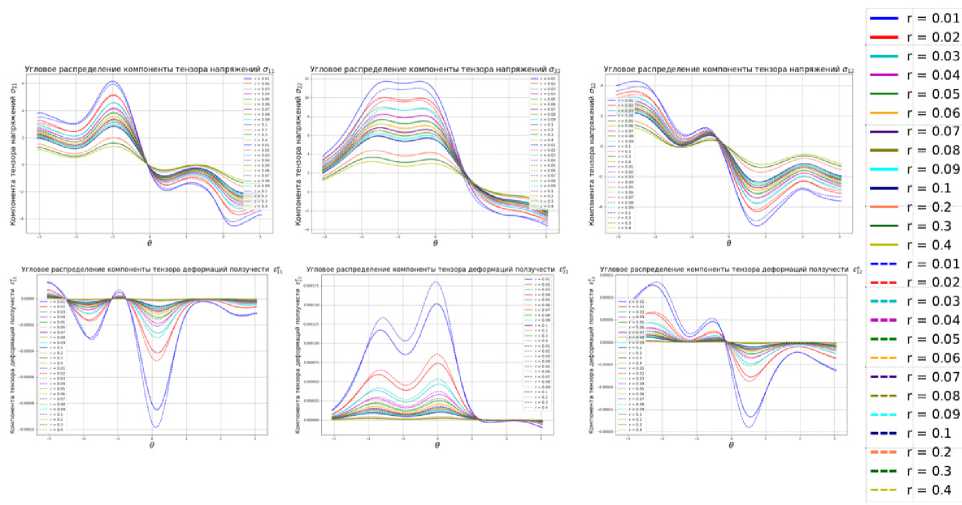
Рис. 13. Угловые распределения тензоров напряжений и деформаций для случая наклонной трещины углом 45° к горизонтали

Fig. 13. Angular distributions of stress and strain tensors for the case of an inclined crack with an angle of 45° to the horizontal

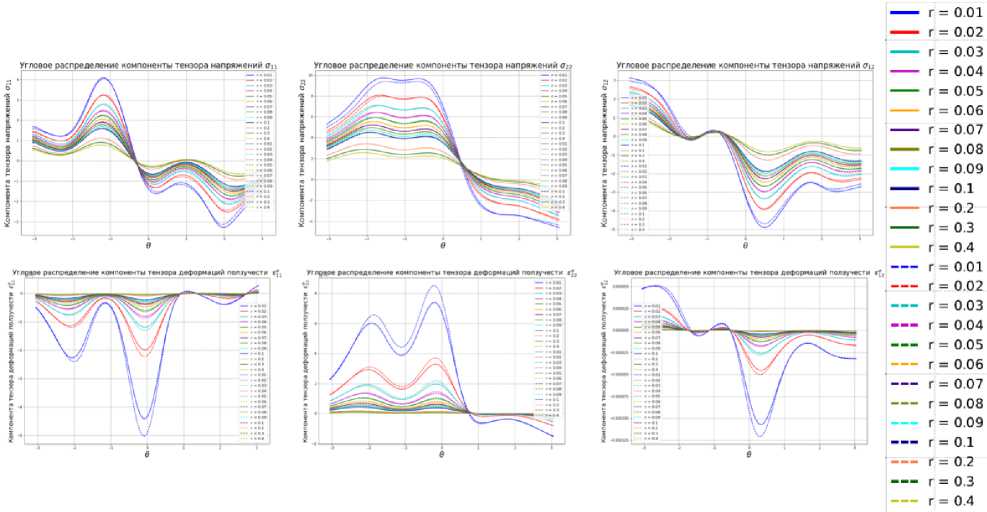
Рис. 14. Угловые распределения тензоров напряжений и деформаций для случая наклонной трещины углом 60° к горизонтали

Fig. 14. Angular distributions of stress and strain tensors for the case of an inclined crack with an angle of 60° to the horizontal

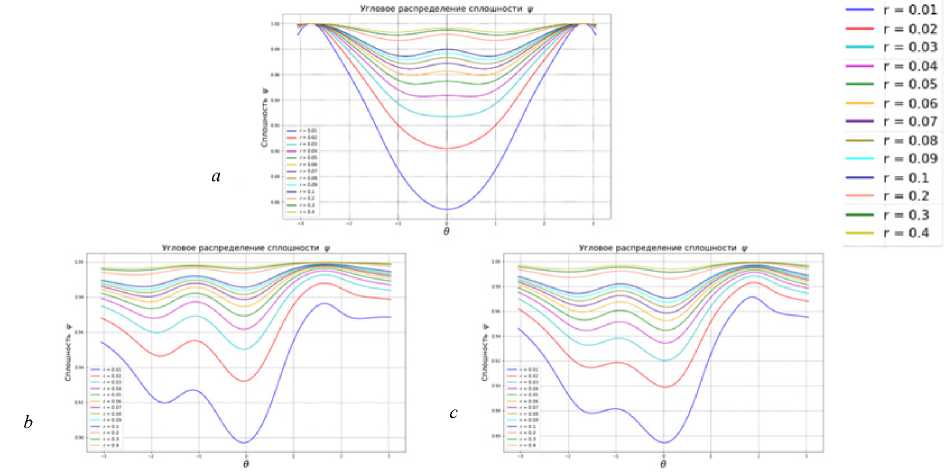
Рис. 15. Угловые распределения параметра сплошности для случая горизонтальной трещины ( а ), для случая наклонной под углом 45 градусов трещины к горизонтали ( b ); для случая наклонной углом 60 градусов трещины к горизонтали ( c )

Fig. 15. Angular distributions of the continuity parameter for the case of a horizontal crack ( a ), for the case of a crack inclined at an angle of 45 degrees to the horizontal ( b ); for the case of a crack inclined at an angle of 60 degrees to the horizontal ( c )

Рис. 15 показывает угловые распределения скалярного параметра сплошности на различных расстояниях от кончика трещины. На графике под литерой « а » приведены симметричные угловые распределения сплошности у вершины трещины нормального отрыва. Видно, что чем больше расстояние от кончика трещины, тем ближе распределение сплошности к единице. Чем меньше расстояние, тем больше активно накапливается поврежден-ность и сплошность уменьшается. Такая же закономерность очевидна на рис. 15 под литерами « b » и « c ».

Следующим шагом анализа является построение радиальных распределений механических полей. Следует отметить, что классическим решением нелинейной механики разрушения (классическим асимптотическим решением полей вблизи вершины трещины в условиях ползучести) является решение, основанное на решении Хатчинсона – Райса – Розенгрена [27–29]:

( C. \1'(r+1)

° j ^{( r} , ^{0 ) =} l ~ITr I      ^d"^{( 0} , ⁿ )

\ r П )

(     * X ^r /( ^{r + 1)}

s j ( r , 0 ) = B |-M S j ( 0 , r ),

I BIrr )

* rn /( r + 1)

u, (r , 0 ) = B I I         r ^{1/( r + 1)} u ( 0 , n ),

I BIr)

(             3 игI

C* =   W*dx, - a,,r,    ds L

'I 2 j i dx1)

G j d S y ,

ставшее основой многих современных исследований [30–34]. Выясним, проявляет ли полученное численное (конечно-элементное) решение асимптотический харак- тер. Сначала исследуется случай ползучести без учета процесса накопления повреждений.

С этой целью построены радиальные распределения нормальной компоненты c ₂₂ вдоль линии продолжения трещины. Построение выполнено для острой трещины и для трещины с конечным радиусом закругления вершины. Путь, вдоль которого строятся радиальные распределения в окрестности острой трещины, приведен на рис. 16 слева, а в окрестности трещины с закругленными вершинами – на рис. 16 справа. На рис. 17 изображены итоги вычислений в пакете SIMULIA ABAQUS, реализующем метод конечных элементов, для четырех различных моделей с острой центральной трещиной с различными материальными константами. Распределение компоненты тензора напряжений a ₂₂ приведены в различные моменты времени и соответственно отмечены разными цветами.

Для модели с острой центральной трещиной получено численное решение и распределения напряжений в двойных логарифмических координатах. Для каждого графика на рис. 17 построена прямая черная линия, аппроксимирующая значения компоненты тензора напряжений a ₂₂ в последний момент времени в зоне ползучести. Полученные значения коэффициента наклона этих прямых соответствуют значениям асимптотики Хатчинсона - Райса - Розенгрена (ХРР): к = - 1/ ( r + 1). Линия, аппроксимирующая значения компоненты тензора напряжений a ₂₂ в зоне упругости, имеет при этом коэффициент наклона, равный к = - 1/ 2 , что также соответствует аналитическому решению классической механики хрупкого разрушения.

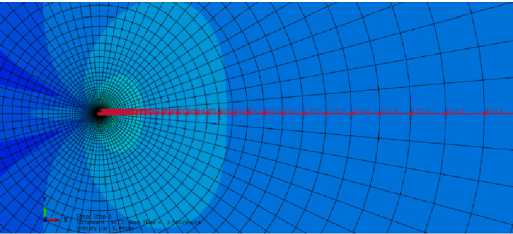
Рис. 16. Путь, вдоль которого строятся радиальные распределения в образце с острой трещиной (слева); путь, вдоль которого строятся радиальные распределения в образце с трещиной с закругленными вершинами (справа)

Fig. 16. The path along which radial distributions are plotted in a sample with a sharp crack (left), the path along which radial distributions are plotted in a sample with a crack with blunted tip (right)

n = 2

n = 4

= 96 45

= 296.5

= 596.5

= 1096

=35000

• - 0 И3298Х+ 0.564853

= 268,3

= 568.3

= 1068

= 2068

= 35000

—-0.250S44X+ 0.558267

n = 3

• ■0.19685 7x+ 0.031338

* t = 7727

t = 12727

• •    t = 22727

• •    t = 35000

  --- у—0.166514X+ 0.564080

n = 5

Рис. 17. Результаты конечно-элементного анализа: компонента тензора напряжений σ 22 в условиях ползучести: распределение напряжения в окрестности вершины острой трещины с течением времени в двойных логарифмических координатах

Fig. 17. Results of finite element analysis: stress tensor component σ 22 under creep conditions: stress distribution in the vicinity of the tip of an acute crack over time in double logarithmic coordinates

Графики уверенно свидетельствуют о том, что численное конечно-элементное решение задачи выходит на асимптотическое решение ХРР в расчетах для острой трещины в условиях ползучести. На рис. 18 изображены поля компоненты тензора напряжений σ22 в двойных логарифмических координатах с течением времени вдоль траектории, показанной на рис. 16 справа, в окрестности трещины с закругленными вершинами в условиях ползучести для различных значений показателя ползучести. Асимптотика в выделенной центральной части на всех графиках соответствует асимптотике ХРР k = –1/(n+1) (решение (3)). В случае установившейся ползучести без учета процесса накопления повреждений конечно-элементное решение явственно обладает асимптотическим поведением классического решения Хатчинсона – Райса – Розенгрена. Также можно отметить, что в области, близкой к вершине закругленной трещины, асимптотика не наблюдается, в отличие от расчетов с острой трещиной. Отсутствие асимптотики ХРР обусловлено влиянием близости затупленной вершины трещины. Правый участок всех кривых на рис. 18 соответствует асимптотике линейно упругого решения. Влияние процессов накопления повреждений отражает рис. 19, где также в двойных логарифмических координатах показана зависимость компоненты тензора напряжений σ22 в области активного накопления повреждений. Графики на рис. 19 отчетливо показывают наличие асимптотического поведения напряжения в центральной области. Наклон кривых для всех рассмотренных значений показателя ползучести отличается от асимптотики решения ХРР. Таким образом, можно утверждать, что процесс накопления повреждений при- напряжений, соответствующего решению ХРР. Наблюдается более слабая сингулярность поля напряжений.

На рис. 20 показаны радиальные распределения сплошности у вершины трещины для различных значе-

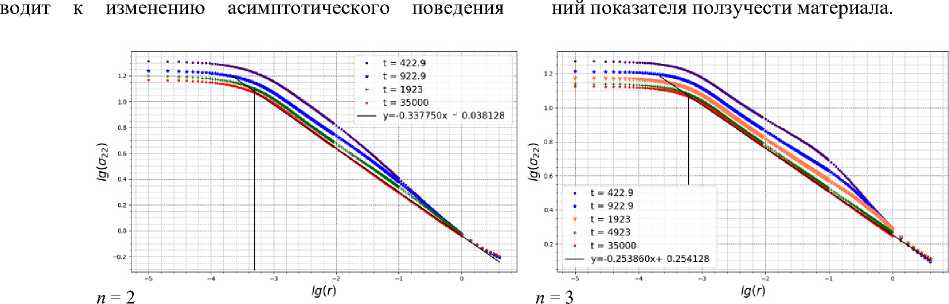
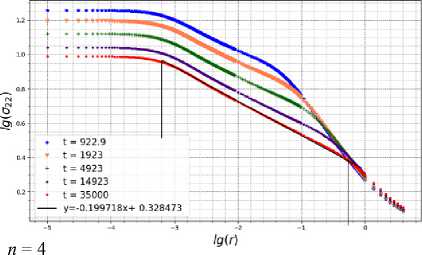
Рис. 18. Результаты конечно-элементного анализа: компонента тензора напряжений σ 22 в условиях ползучести: радиальное распределение напряжения σ 22 у затупленной вершины трещины с течением времени

Fig. 18. Results of finite element analysis: stress tensor component σ 22 under creep conditions: radial stress distribution at the blunted crack tip over time

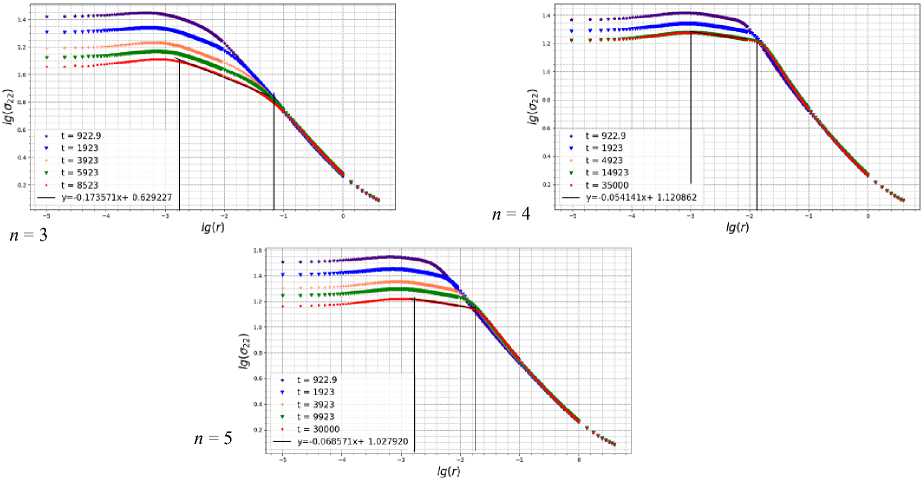
Рис. 19. Результаты конечно-элементного анализа: радиальные распределения компоненты тензора напряжений σ 22 в условиях при действии процесса накопления поврежденности c течением времени

Fig. 19. Results of finite element analysis: radial distributions of stress tensor component σ 22 under conditions under the action of damage accumulation process over time

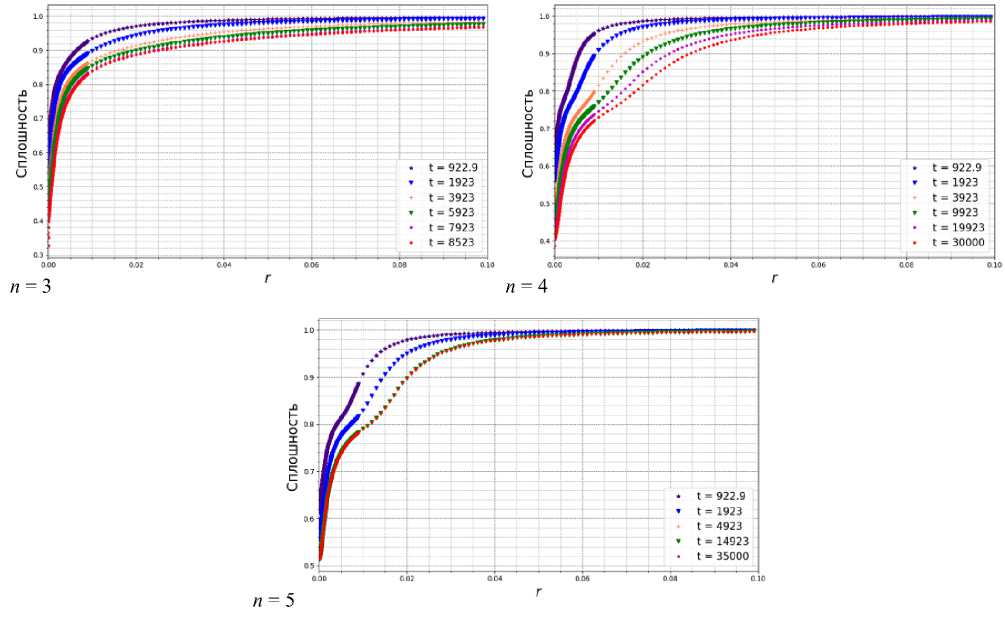
Рис. 20. Радиальные распределения сплошности у вершины трещины для различных значений показателя ползучести материала

Fig. 20. Radial continuity distributions at the crack tip for different values of the creep exponent of the material

+ 2 000 ч (с учетом поврежденности)

2 000 ч (без учета поврежденности)

° 10 000 ч (с учетом поврежденности) 10 000 ч (без учета поврежденности)

Рис. 21. Радиальное распределение нормальной компоненты напряжений σ 22 на продолжении трещины отрыва в двойных логарифмических координатах для n = 5

Fig. 21. Radial distribution of the normal stress component σ 22 on the continuation of Mode I crack in double logarithmic coordinates for n = 5

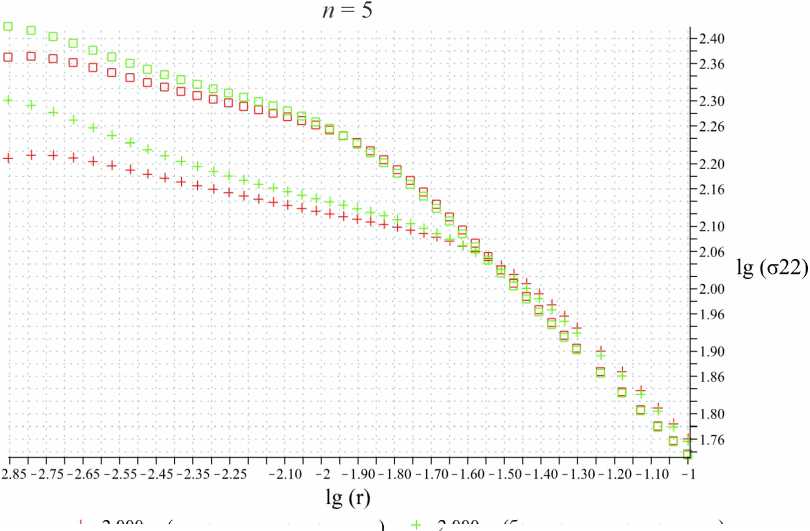
Для большего разъяснения асимптотического поведения решения вблизи вершины трещины ниже приводятся результаты расчетов для целой серии различных материалов с материальными постоянными, полученными на основании экспериментальных данных и сведенных в таблицы [15]. На рис. 21 показаны радиальное распределение нормальной компоненты напряжений σ22 на продолжении трещины отрыва в двойных логарифмических координатах для n = 5. Зеленым цветом показана кривая зависимости напряжения σ22 от радиальной координаты для расчета без учета поврежденности. Красным цветом показаны результаты расчета при ис- пользовании пользовательской процедуры UMAT, в рамках которой осуществляется интегрирование кинетического уравнения Качанова – Работнова. Видно, что оба процесса выходят на прямую, что явственно свидетельствует об асимптотическом поведении распределения напряжений, но наклон двух прямых различен. Зеленые точки, полученные в ходе вычислительного эксперимента, полностью соответствуют асимптотике ХРР, тогда как красные точки также выстраиваются вдоль прямой, но с меньшим наклоном, т.е. влияние повре-жденности приводит к снижению особенности, свойственной решению ХРР. На рис. 22–24 показаны радиальные распределения напряжения у вершины трещины в условиях ползучести для различных значений показа- теля ползучести материала n = 5, 7, 9. Слева на каждом графике показаны распределения напряжения в двойных логарифмических координатах без учета накопления повреждений, тогда как справа приведены распределения, отвечающие учету процесса деградации сплошности. Из рис. 21–24 явствует, что процесс накопления повреждений приводит к изменению (к снижению) сингулярности поля напряжений в зоне активного накопления повреждений. Непосредственно показатель степенной асимптотики полей напряжений и сплошности, по всей видимости, можно найти, построив асимптотические разложения в окрестности вершины, прибегая к методу разложения по собственным функциям [36; 37], что и будет направлением дальнейшей работы.

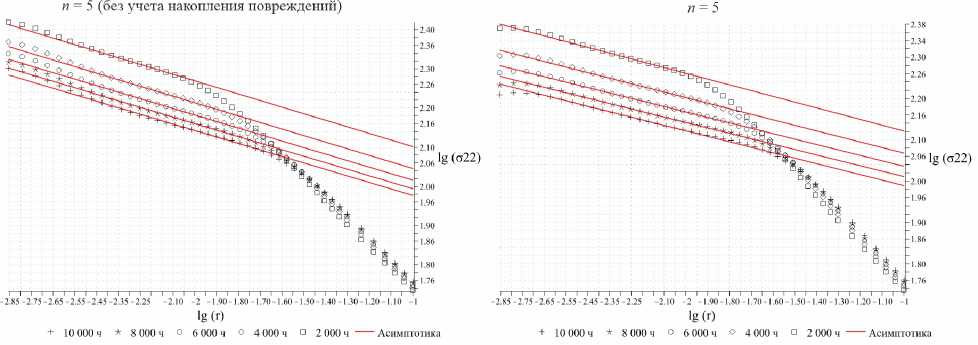
Рис. 22. Радиальное распределение нормальной компоненты напряжений σ 22 на продолжении трещины отрыва в двойных логарифмических координатах для n = 5 (слева: без учета поврежденности; справа: с учетом процессов накопления повреждений)

Fig. 22. Radial distribution of the normal stress component σ 22 on the continuation of Mode I crack in double logarithmic coordinates for n = 5 (left: without taking into account damage; right: taking into account the processes of damage accumulation)

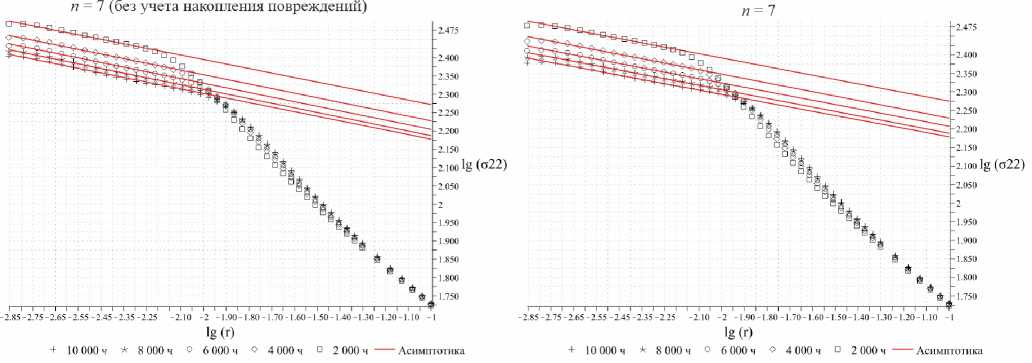
Рис. 23. Радиальное распределение нормальной компоненты напряжений σ 22 на продолжении трещины отрыва в двойных логарифмических координатах для n = 7 (слева: без учета поврежденности; справа: с учетом процессов накопления повреждений)

Fig. 23. Radial distribution of the normal stress component σ 22 on the continuation of Mode I crack in double logarithmic coordinates for n = 7 (left: without taking into account damage; right: taking into account the processes of damage accumulation)

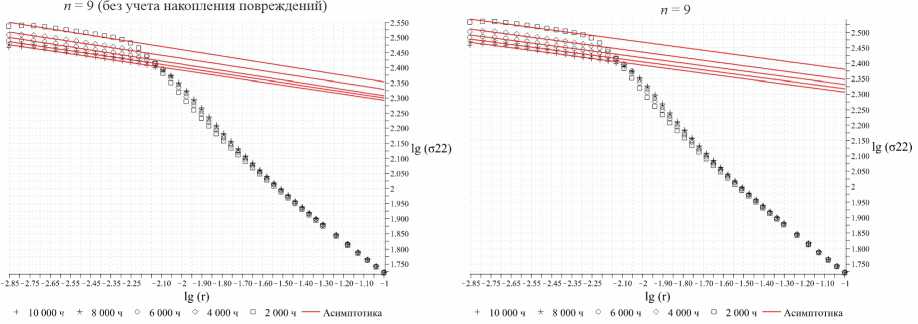
Рис. 24. Радиальное распределение нормальной компоненты напряжений σ 22 на продолжении трещины отрыва в двойных логарифмических координатах для n = 9 (слева: без учета поврежденности; справа: с учетом процессов накопления повреждений)

Fig. 24. Radial distribution of the normal stress component σ 22 on the continuation of Mode I crack in double logarithmic coordinates for n = 9 (left: without taking into account damage; right: taking into account the processes of damage accumulation)

Заключение

Разработана и применена пользовательская процедура UMAT для включения модели Качанова – Работ-нова в вычислительную схему метода конечных элементов, реализованную в расчетном пакете SIMULIA Abaqus. Определены поля напряжений, деформаций ползучести и сплошности у вершины трещины в соответствии с эволюционным уравнением модели Качанова – Работнова для целого ряда материалов. Из выполненного конечно-элементного анализа и сравнения полученных распределений напряжений и деформаций ползучести, рассчитанных без учета процесса накопления повреждений и с его учетом, следует, что присутствие повреждений сказывается как деградация всех прочностных характеристик твердого тела: при прочих равных условиях все величины, инвариантно описывающие напряженное состояние, отличаются в сторону