Влияние эффекта Доплера на вероятность ошибки в системе приема сигнала на одну и на две антенны

Эффект Доплера оказывает большое влияние на вероятность битовой ошибки, особенно в низкоорбитальных спутниковых системах. Так, например, для спутника, вращающегося по круговой орбите и находящегося на высоте 700 км, скорость движения составляет около 7,5 км/с. Время видимости таких спутников очень ограничено. И в моменты, когда спутник появляется на радиогоризонте и уходит за него, модуль радиальной проекции его вектора скорости на потребителя максимален, возникает доплеровский сдвиг частоты порядка 7 кГц, при частоте сигнала порядка 1,6 ГГц. Таким образом, происходит отклонение несущей частоты и всего спектра от номинального значения. Номинальное значение несущей частоты формирует местный генератор (гетеродин) на приемнике и, поскольку частóты (принятого сигнала и местного) не совпадают, возникает расхождение, приводящее к погрешности.

На сегодняшний день для снижения ошибки, вызванной эффектом Доплера, применяется автоматическая подстройка частоты (АПЧ). Системы АПЧ обладают некоторой инерционностью и полностью не позволяют исключить ошибку, обусловленную эффектом Доплера. Разнесенный прием, как будет показано ниже, позволяет при малых значениях частоты Доплера эффективно снизить вероятность ошибки.

В результате действия доплеровского сдвига частоты при приеме сигналов двоичной относительной фазовой телеграфии (манипуляции) ОФМ-2 возникает ошибка, вероятность которой [1–3] описывается выражением:

р ₌ р0 ' ( 1 - Jо ( ² ‘М, • T ) )        (1)

где ρ ₀ – это среднее значение отношения сигнал/шум;

f_d – текущий доплеровский сдвиг, Гц;

J ₀(2 π ⋅ f_d ⋅ T ) – корреляционная функция синфазной или квадратурной компоненты соответствующего гауссовским замираниям комплексного

Том 2

процесса [4–6], сдвинутого на время Т , находится через функцию Бесселя нулевого порядка;

Т – длительность одного информационного символа, а также время задержки сигнала при демодуляции сигнала ОФМ-2, с.

Разнесенный прием возможен по частоте, по поляризации, по стороне разнесения, по углу, по времени и по пространству [1; 7; 8]. Разнесенный прием по частоте и по времени активно применяется в навигационных системах, но он требует дополнительного частотного ресурса или ограничивает по времени количество передаваемой информации. Поляризационный разнесенный прием является либо частным случаем пространственного, так как требуется две отдельные антенны для двух перпендикулярных составляющих, либо имеет дополнительные потери 3 дБ при приеме сигнала на одну антенну. Самым эффективным является метод пространственного разнесения приемных антенн. При обеспечении разности расстояний между антеннами порядка нескольких длин волн сигналы с выходов антенн можно считать некоррелированными и независимыми.

Вероятность ошибки, возникающей вследствие действия доплеровского сдвига частоты, при пренебрежении отношением сигнал/шум при приеме ОФМ-2 сигналов на две антенны описывается выражением [1–3]:

На рис. 1 представлена структурная схема приемника ОФМ-2 сигналов на одну антенну, для которого справедливо (1). На рис. 2 представлена структурная схема приемника ОФМ-2 сигналов на две антенны, для которого справедливо (2) [1; 8; 9].

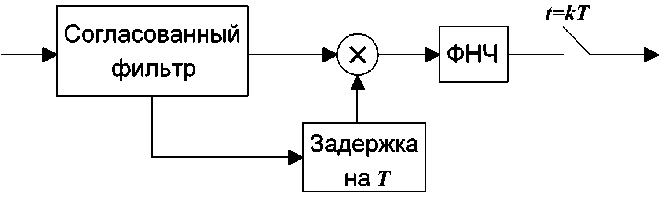
Рис. 1. Схема приемника ОФМ-2

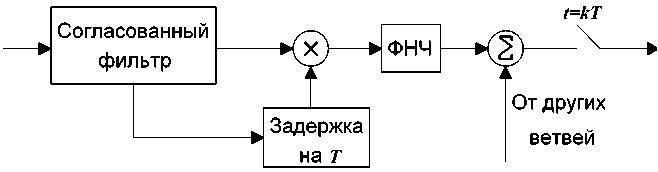
Рис. 2. Схема приемника ОФМ-2 сигналов при приеме на две антенны

Проведем исследование влияния частоты Доплера на вероятность ошибки, а также в общем виде исследуем влияние скорости передачи данных на вероятность ошибки.

На основе (1) и (2) при среднем отношении сигнал шум равным 10 и при скоростях передачи информации 32 кбит/с и 32 Мбит/с построим графики зависимости вероятности ошибки от частоты Доплера.

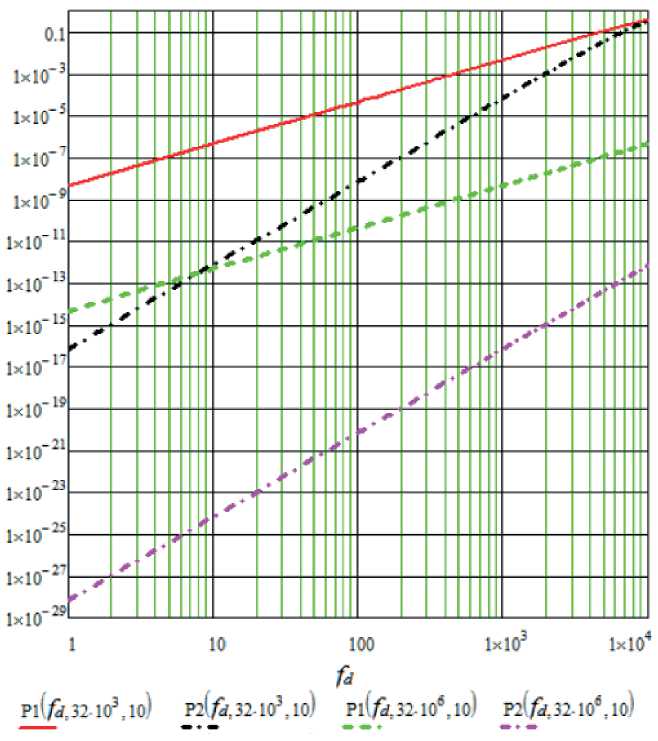
Рис. 3. Вероятность ошибки на двоичный символ из-за доплеровского сдвига частоты

Анализируя зависимости, представленные на рис. 3, заметим, что при малом значении доплеровского сдвига частоты разнесенный прием на две антенны существенно уменьшает порядок ошибки. Однако, при увеличении частоты Доплера, эффективность системы разнесенного приема падает. Например, при частоте Доплера 1 кГц и скорости 32 кбит/с вероятность ошибки уменьшается уже меньше чем на 2 порядка, а при частоте Доплера 7 кГц величины имеют уже один порядок и различие между ними всего в 1,5 раза. Кроме того, из представленных графиков для разных скоростей передачи 32 кбит/с и 32 Мбит/с очевидно, что чем быстрее передается информация, тем меньше вероятность ошибки, вызванная частотой Доплера. Например, для приема сигнала на 1 антенну и скорости передачи информации 32 кбит/с и 32 Мбит/с разность в вероятности ошибки составляет 6 порядков, а при приеме сигнала на 2 антенны уже около 12 порядков.

Для того чтобы исследовать эффективность разнесенного приема при различных скоростях передачи информации усредним влияние частоты Доплера. Для усреднения влияния мгновенной частоты Доплера рассмотрим вопрос о том, как меняется дополнительный частотный сдвиг для наблюдателя.

Существует известная формула для частоты Доплера:

Г и fa = т             (3)

л

с где л = — - длина электромагнитной вол ны, м; f – частота электромагнитной волны, Гц;

c – радиальная скорость спутника, скорость спутника в направлении на точку наблюдения, м/с.

Согласно (3), частотный сдвиг определяется радиальной скоростью спутника, мгновенное значение которой найдем, используя рис. 4.

Время приема спутникового сигнала определяется временем прямой видимости спутника над линией радиогоризонта. В моменты появления и ухода спутника за радиогоризонт модуль его радиальной составляющей скорости максимален, а при прохождении спутника над наблюдателем равен нулю. В общем виде угловая зона B ₀ и время видимости спутника Δt зависят от высоты орбиты спутника и определяются выражениями [10]:

• B 0 = arccos Rz cos ^ m™) ^- « min ,     ⁽⁴⁾

Rz + h где Rz = 6371 – радиус Земли, км;

h = 700 – высота орбиты спутника, км;

α _min – угол отсечки по высоте, минимальный угол радиовидимости спутника, рад.

∆ t = ^{2 ⋅ B} 0 ,                (5)

ω

V где to =------- угловая скорость спутника,

Rz + h рад/с.

Скорость движения спутника определяется как первая космическая скорость по формуле:

_тл G • Mz „

V =         = 7,523 , км/с (6)

Rz + h где Mz = 5,972⋅1024 – масса Земли, кг;

G = 6,67 ⋅ 10^-11 – гравитационная постоянная, м³ ⋅ кг^-1 ⋅ с^-2.

Согласно рис. 4 видим, что радиальная скорость спутника определяется синусом угла A между вектором скорости спутника и направлением, перпендикулярным направлению на наблюдателя:

u _r = V • sin( A )^^^^^H (7)

Теперь получим аналитическую запись для нахождения угла А исходя из того, что:

• 1)    Вектор скорости спутника перпендикулярен направлению на центр Земли, т.е. ∠ АА’C = π /2;

• 2)    Т.к. спутник движется равномерно по круговой орбите вокруг Земли, вектор В , проведенный из центра Земли на спутник, движется равномерно с угловой скоростью ω ;

  

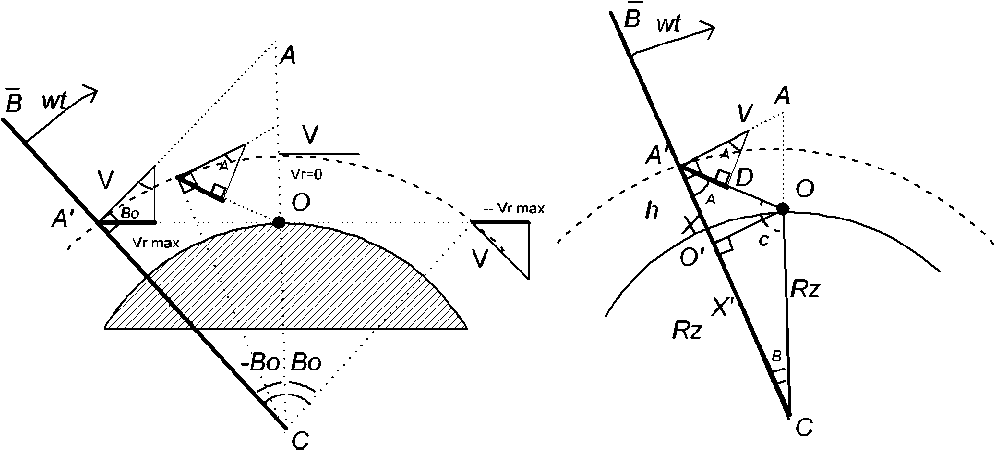
  Рис. 4. Пояснение к нахождению радиальной скорости спутника

  
  
  
  

  • 3)    При движении вектора В сигнал от спутника начинает приниматься от угла - B ₀ до угла B ₀.

  Начнем рассуждения:

  • 1)    Искомый угол А лежит в треугольнике A’VD, в котором Z VA’D = п /2 - A .

  • 2)    Т.к. Z AA’C = п /2, то его составляющие Z VA’D + Z CA’D = п /2, из чего следует, что Z CA’D = п /2 - Z VA’D = п /2 - п /2 + A = A .

  • 3)    Таким образом дальше будем искать выражение для записи угла A = Z CA’D= Z CA’O в зависимости от угла В = - В ₀ + tot .

  • 4)    Т.к. мы точно знаем две стороны треугольника СA’, CO и угол между ними B = Z A’CO, то мы можем точно найти искомый

  
  

  Том 2

  угловая скорость спутника to = 1,064 - 10^-3,

  

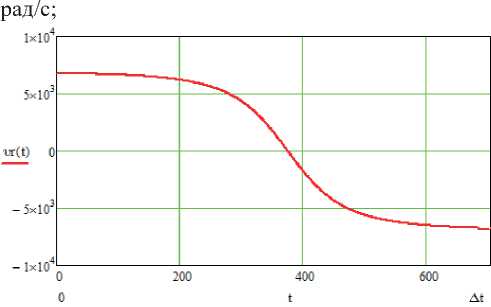
  Рис. 5. График радиальной скорости спутника

  
  

  угол. Для этого проведем перпендикуляр О’О, разделив треугольник CA’O на два прямоугольных треугольника CО’O и A’О’O.

  • 5)    Размер перпендикуляра определяется синусом угла В по формуле: O’O= Rz - sin( B )=

  Rz - sin(- B ₀+ tot ).

  • 6)    Перпендикуляр делит сторону СА’ длиной Rz + h на две части: A’O’ длиной Х и СО’ длиной

  
  

  Х', и определяемую косинусом угла В по формуле: Х’= Rz - cos( B )= Rz - cos(- B ₀+ tot ).

  • 7)    Таким образом, СО’=Х= Rz + h – X’= Rz + h - Rz - cos(- B ₀+ tot ).

  • 8)    Зная размеры сторон O’O и СО’, можем найти искомый угол A = Z O’A’O по (80):

  
  

  Используя полученное выражение (9), усредним влияние эффекта Доплера на вероятность ошибки для всего периода наблюдения спутника.

  Для этого найдем общую среднюю вероятность ошибки на бит как интеграл по времени от (1) и (2) соответственно для приема сигнала на одну и две антенны, вместо частоты Доплера подставим (3), где радиальную скорость запишем по (9), полученные интегралы нормируем по времени. Получим (10) и (11).

  Построим графики по (9) и (10) от скорости

  
  

  A = arc tg

  
  

  O ' O

  A ' O '

  
  

  = arc tg

  
  

  Rz • sin ( - B₀ + to t )

  Rz + h - Rz • cos ( - B 0 + to t )

  
  
  
  

  Объединим (7) и (8) и получим выражение для нахождения радиальной скорости спутника от времени. Для учета того, что когда спутник приближается к наблюдателю частотный сдвиг больше нуля, и когда спутник отдаляется частотный сдвиг меньше нуля, а синус отрицательного угла sin(- B ₀) меньше нуля, введем в формулу «-1»:

  U r (t ) = V • ( - 1) •

  
  
  

  Р»(Л,рО) Psr2(/j,p0)

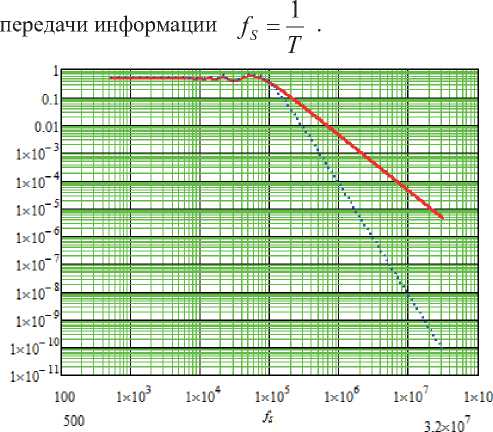
  Рис. 6. Зависимость средней вероятности ошибки на бит от скорости передачи данных

  
  

  • sin arc tg

  
  

  Rz • sin( - B ₀ + ro t )

  Rz + h - Rz • cos ( - B ₀ + ro t )

  
  
  
  

  Построим график радиальной скорости спутника по (9). Задав угол отсечки по высоте 3 ° , получим:

  минимальный угол радиовидимости спут-

  ^п

  ника « mm = ³ TZZ , рад;

  угол видимости спутника B ₀ = 0,399, рад;

  время видимости спутника Δt = 750,41, с;

  
  

  Проанализируем среднюю вероятность ошибки на бит в зависимости от скорости передачи информации по рис. 6. При скорости передачи информации около 1 Мбит/с разнесенный прием позволяет снизить среднюю вероятность ошибки на бит примерно на 2 порядка, а при скорости 32 Мбит/с разница составляет почти 5 порядков.

  
  
  
  

  Р о •

  
  
  
  

  V • ( - 1) • sin arc tg

  2n-

  
  

  Rz • sin( - B ₀ + to t )

  Rz + h - Rz • cos ( - B 0 + to t ) T

  X

  
  

  \

  
  
  
  

  Д t

  P 1 = -If
  
  ^Д t {

  
  

  к      к

  
  

  V

  
  

  — dt

  
  
  
  
  
  

  V • ( - 1) • sin arc tg

  
  

  Rz • sin( - B ₀ + to t )

  
  
  
  

  0,25 •

  
  

  Д t

  P 2 = -

  A t J

  
  

  _•

  
  
  
  
  
  
  

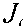
  2n

  
  

  к

  
  

  V • ( - 1) • sin arc tg

  2.Л--------

  
  

  к

  
  

  Rz + h - Rz • cos ( - B ₀ + to t )

  I

  
  

  Rz • sin( - B ₀ + to t )

  Rz + h - Rz • cos ( - B _o + to t ) ----------_^°---^ • t

  I

  
  

  7

  M

  
  

  dt

  
  
  
  
  
  

  7

  
  

Прием цифровых спутниковых сигналов относительно сильно ухудшается ввиду доплеровского смещения частоты. В статье проанализирована эффективность повышения помехоустойчивости за счет применения разнесенного приема. В качестве оцениваемого спутникового сигнала, был выбран сигнал с частотой 1,6 ГГц спутника, движущегося по круговой орбите высотой 700 км, вид модуляции DBPSK.

Используя (1) и (2) на рис. 3 было показано, что при использовании разнесенного приема мож- но уменьшить вероятность ошибки на бит в 2 раза при малых значениях частоты Доплера, а при значениях частоты Доплера, равных максимальному значению, система разнесенного приема эффективнее примерно в 1,5 раза.

Также в статье было проведено усреднение влияние эффекта Доплера и показана эффективность системы разнесенного приема. Например, при скорости передачи информации 32 Мбит/с разнесенный прием позволяет уменьшить порядок ошибки примерно в 2 раза.