Исследование центробежных моментов инерции рабочих органов мелиоративных машин и боковых динамических реакций на их опоры при работе на склонах

При работе мелиоративной техники на откосах каналов, как правило, базовая силовая установка располагается на дамбе канала, а рабочее оборудование – на откосе (склоне). Вследствие этого происходят изменения центробежных моментов инерции рабочих органов мелиоративных машин и боковых динамических реакций на их опоры. Изменения центробежных моментов инерции рабочих органов и боковых динамических реакций на их опоры зависят от угла заложения откосов, то есть от угла наклона рабочего органа. Все вышеизложенное необходимо учитывать при проек- тировании мелиоративной техники на предмет ее работоспособности и безопасности эксплуатации в заданных условиях. Проведем теоретические исследования изменения центробежных моментов инерции рабочих органов и боковых динамических реакций на их опоры на примере шнековой мелиоративной косилки.

Режущий аппарат (РА) мелиоративной косилки имеет плоскость материальной симметрии x z , совмещенную с плоскостью рисунка (рис. 1).

При опускании РА на откос канала мы имеем осевые моменты инерции l и l относительно осей z и х , проходящих через центр тяжести О РА и лежащих в плоскости материальной симметрии x z , а также центробежный момент инерции l .

Нам необходимо определить центробежные моменты инерции РА мелиоративной косилки, l , l , l , если оси z и х xz     yz     xу                        1         1

повернуты относительно осей z и x на угол а , равный углу наклона окашиваемой поверхности.

Ось y перпендикулярна к плоскости материальной симметрии x z и поэтому является главной осью инерции в точке О .

Тогда в ноль обращаются два центробежных момента инерции, т.е.

l = l = 0.(1)

yzyx

Вычисляем центробежный момент инерции l , который равен [1]: n l = У m, x, z, .(2)

xz             k k k k=1

Выразим координаты x и z в зави симости от x и z , для чего воспользуемся формулами аналитической геометрии преобразования координат при повороте осей на угол а [2]:

z = z cosa - x sin а, x = zx sin a + x cosa.          (3)

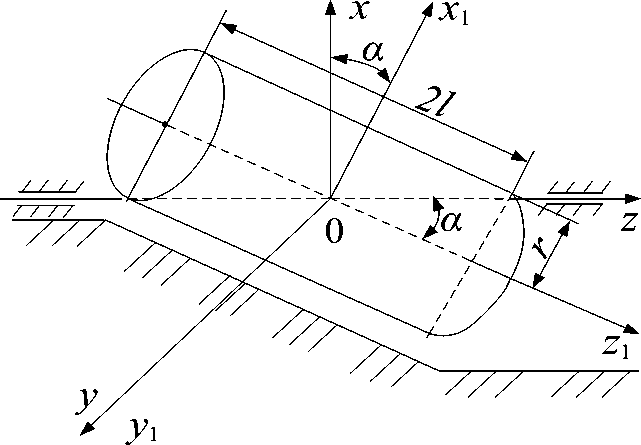
Рис. 1. Схема для определения центробежных моментов инерции цилиндрического режущего аппарата при работе на откосе канала

Эти формулы даны с учетом, что поворот осей совершен против часовой стрелки. Учитывая, что в нашем случае поворот осей осуществляется по часовой стрелке, заменим в формулах (3) угол а на

— а . Тогда для к -й точки получим:

z, = z., cosa + x .sin а, x, =— z. .sin а + x, cosa.(4)

k        1k                   1k            ,       k           1k1

Подставив значения (4) в формулу (2), получим:

nn l = У m,x,z, = У m, (— z., sin а + x.,cosa)x(z., cosa + x., sin а).

xz              k k k              k       1k                 1k                    1k1

k=1

Путем математических преобразований получим:

l

xz

sin 2 а

n

E m^x 2

k  1k k=1

n

- ^mkz 2k k  1k k=1        7

n

+ cos2 a ^ m k z i k x i k .

k = 1

Добавим и отнимем в

n круглой скобке формулы (5) X my^.

к = 1

Тогда

_ sin 2a xz =   2

n

nn   n

X m ( x k + y 2 ) - X m ( z k + ^ ) + cos2 a X

_ k = 1

k = 1

k = 1

mzx . k 1 k 1 k

Но x ,², + y 2 = d 2 - квадрат расстояния k -й точки до оси z. , а z ,², + y ² = d ²   -

1 k        1 k         kz ₁                                                                                      1           1 k        1 k         kx ₁

квадрат расстояния k -й точки до оси х , тогда получим:

l

xz

sin 2 a f

2    <

nn

E m,d 2 — X m^d^

k   kz ₁                k   kx ₁

k = 1                  k = 1

)

n

+ cos2aX m,z.,x., .

k 1k 1k k=1

nnn

Так как на самом деле у m,d,  = l , 7 m,d,  = l , 7 m,z.,x., = l , k kz1       z1              k kx1       x1              k 1k 1kx k=1                          k=1

то формула (6) примет вид:

,           , \sin2a , ,

l = ( l - 1 ) + 1   cos2 a .

xz        z1       x1

Итак, центробежные моменты инерции для работающего на откосе канала РА определяются по формулам (1) и (7) и соответственно равны:

l„ = l „ = 0 , l₌ = ( l_z, - 1, , ) ^sin ² " + 1    cos2 a .

yz     yx          xz      z1     x1

Но при нахождении РА на откосе канала z является его осью материальной симметрии. Вычислим центробежный момент инерции шнекового РА, который представлен как однородный круглый цилиндр массой М , радиуса r и длиной 2 l .

Ось z , будучи осью материальной симметрии, является главной осью инерции, следовательно:

^lz 1 x 1 = ^lx 1 У 1 = ⁰ .

Значит, формула (7) примет вид:

,           \sin 2 a

• l    =(l -1 )--------.(8)

xz        z1

Основные моменты инерции одно- родного круглого цилиндра равны

Mr2        /r2

l z 1 =^ , ^lX 1 = M Y ⁺ T [1]. ^Под-

• 2           k 43

  ставив эти значения

  
  

  в формулу (8), полу-

  
  

  l xz = M

  
  

чим:

r l   sin 2a

---- k 4   3 J 2

Итак, центробежные моменты инерции РА однородной цилиндрической формы определяются по формулам (1) и (9):

^lyz ^lyx ⁰ , ^lxz

Для нахождения динамических боковых давлений на опоры РА косилки, работающей на откосе канала, зададимся следующими условиями. РА (рис. 2) весом Р , радиуса r и длиной 2 l вращается с постоянной угловой скоростью to вокруг оси z , проходящей через его центр тяжести О .

= M —

4 k

l ² ) sin 2 a —

• 3    J 2

Ось вращения z РА образует с его осью симметрии Z угол a .

Нам необходимо определить боковые динамические давления на опоры A и B , если ОА = ОВ = h .

Подвижные оси x , у , z связаны с

цилиндрической формой РА. Центробежные моменты инерции РА определяются по формулам (1) и (9) и соответственно равны:

l yz = 0 .

lxz

P- ( r2

2 g ( 4

^-

1 2 ^

— sin 2a .

Центр тяжести С цилиндра находит-

Оперируя формулами (1), (9), (10) и (11), составим систему уравнений для определения величин, составляющих динамических боковых давлений N Ax , N Ay , N Bx , N By :

N x + N x = 0,

N y + N. = 0,

N y h - N By h = 0,

ся на оси z , следовательно,

X c = У с = 0 .         (10)

Так как РА вращается равномерно, то

£ = 0 .             (11)

P r

-

N^h + N_Bxh =

Ax           2 g ^ 4

-

1 2 )

— to ² sin 2 a .

3 7

Решив эту систему уравнений, получим:

N Ay = N By = 0,

N Bx =

^-

■ Nax =

P

r

^-

4 gh ( 4

to ² sin 2 a .

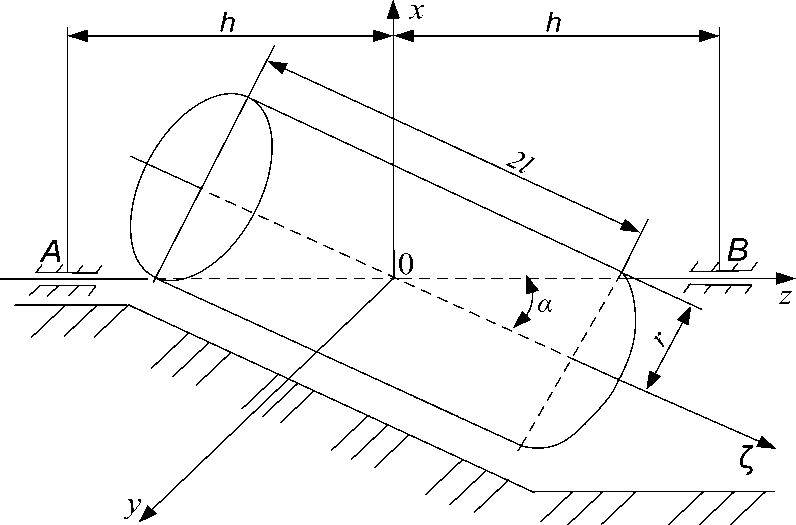
Рис. 2. Схема для определения боковых динамических давлений на опоры цилиндрического режущего аппарата при работе на откосе канала

При вращении РА создаются динамические боковые давления на опоры A и B , образующие пару сил с плечом AB = 2 h . Боковые динамические реакции опор A и B равны по модулю соответствующим давлениям и направлены противоположно.

По вышеизложенной методике, пользуясь таблицей «Моментов инерции однородных твердых тел», можно вычислить центробежные моменты инерции любого рабочего оборудования мелиоративной техники, а также определить боковые динамические реакции на их опоры.