Исследование деформационного поведения стали 20Х13 в условиях горячей осадки

Хромистые коррозионно-стойкие стали мартенситного класса благодаря высокой прочности используются для изготовления лопаток паровых турбин, цельнокатаных колец различного назначения; различных деталей авиастроения, а также обсадных труб для нефтяных скважин. В процессе производства указанных изделий эти стали подвергаются горячей прокатке, ковке или штамповке. Поэтому важно знать и уметь предсказывать их деформационное поведение в различных температурно-скоростных режимах обработки. Цель настоящей работы – исследовать в лабораторных условиях процессы горячей деформации стали 20Х13 и получить аналитические выражения для максимальных напряжений течения, необходимые для инженерных расчетов.

Материалом исследования служили цилиндрические образцы стали 20Х13 промышленной плавки следующего химического состава: 0,2 % С, 12,6 % Сr, 0,55 % Mn, 0,68 % Si, 0,016 % Р. Одноосное сжатие образцов диаметром 10 мм и высотой 15 мм производилось на модуле Hydrawedge (пластометр) физического симулятора Gleeble-3800 в интервале температур 900–1150 °С (в аустенитной области) и скоростей деформации 0,01–40 с–1. Образцы нагревались до температуры испытания со скоростью 5 °С/с прямым пропусканием электрического тока, выдерживались при этой температуре 15 мин, подвергались деформации и затем ус- коренно охлаждались струей воды. Усилие деформации измерялось тензометрическим датчиком. Деформация фиксировалась датчиком продольной деформации по уменьшению высоты образца. Температура образцов контролировалась термопарой, приваренной к образцу. Отсутствие температурного градиента обеспечивалось использованием специальных бойков с высоким электрическим сопротивлением. Для уменьшения трения между бойками и образцом использовались графитовые вставки.

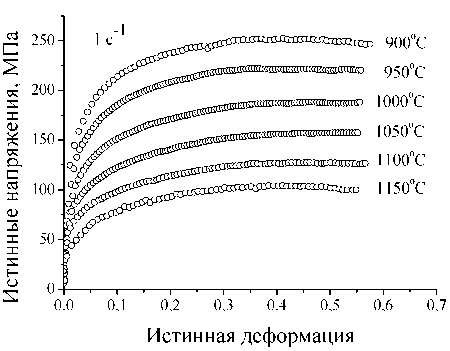
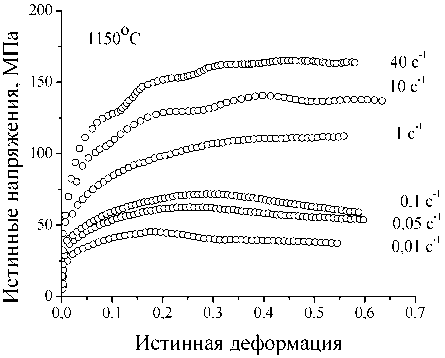
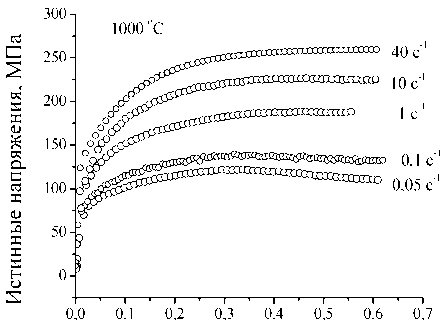
Экспериментальные кривые течения исследуемой стали в координатах истинные деформации ( ε ) – истинные напряжения ( σ ) приведены на рис. 1. В условиях постоянных скоростей деформации е (рис. 1, а, б) напряжения течения падают с ростом температуры деформации. Увеличение скорости деформации при постоянной температуре испытаний сопровождается ростом напряжений течения (рис. 1, в, г). Вид кривых течения, типичный для горячей деформации, также зависит от температуры и скорости деформации. Схематически два наблюдаемых типа кривых течения в пластической области представлены на рис. 2. При относительно низких температурах и высоких скоростях деформации процессы деформационного упрочнения сопровождаются термически активируемыми процессами динамического возврата, заключающимися в перераспределении и

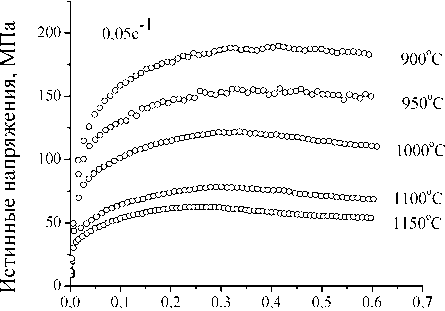
Истинная деформация

б)

а)

в)

Истинная деформация

г)

Рис. 1. Экспериментальные кривые течения стали 20Х13 при разных температурно-скоростных режимах деформации

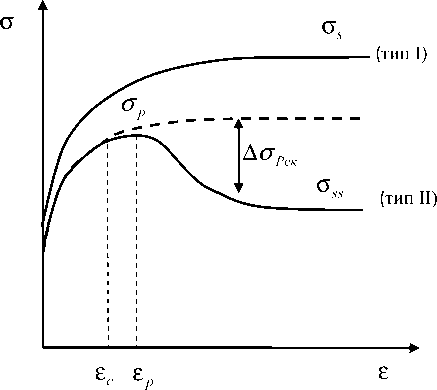
Рис. 2. Типичные кривые течения металлов в условиях динамического возврата (тип I) и динамической рекристаллизации (тип II)

аннигиляции дислокаций. В результате напряжения течения достигают максимума σ _s и при дальнейшем росте степени деформации остаются практически постоянными (выходят на плато) в силу установившегося равенства скоростей размножения и аннигиляции дислокаций (рис. 2, тип I).

При высоких температурах (1000–1150 °С) и малых скоростях деформации (0,01–0,1 с–1) форма кривых течения приобретает иной вид: наблюдается падение напряжений течения после достижения ими пиковых значений σp с последующим выходом на постоянное установившееся значение о55 (рис. 2, тип II). Такое интенсивное разупрочнение свидетельствует о протекании динамической рекристаллизации, начинающейся при некоторой критической степени деформации £c (чуть ниже деформации £p , соответствующей пиковому напряжению оp) и приводящей к установлению нового баланса между процессами упрочнения и разупрочнения.

Для анализа и предсказания деформационного поведения материалов разработаны модели пластического течения, учитывающие реальный механизм деформационного упрочнения, динамического возврата и динамической рекристаллизации [1–3]. В этих моделях совместное влияние температуры и скорости деформации на деформационное поведение металлических материалов описывается параметром Зинера – Холломона:

Z = £ exp | Q— | , (1) ( RT )

где £ и T - соответственно скорость и абсолютная температура деформации, R – газовая постоянная, а Q – энергия активации процесса, контролирующего горячую деформацию. При относи-

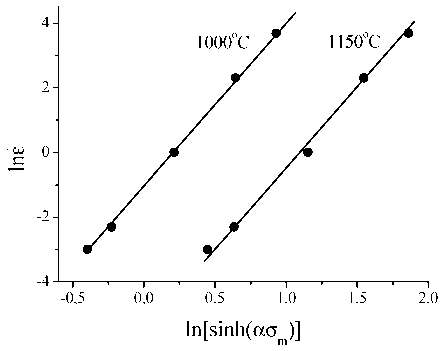
а)

тельно высоких значениях параметра Z (высокие скорости деформации и низкие температуры) единственным механизмом разупрочнения является динамический возврат (рис. 2, тип I), тогда как в случае малых значений параметра Z следует ожидать развитие процессов динамической рекристаллизации (рис. 2, тип II).

Первым шагом в построении модели пластического течения является нахождение энергии активации Q , входящей в параметр Зинера – Хол-ломона, и установление связи между параметром Z и максимальными напряжениями течения о m ( о ₅ - тип I или о p - тип II на рис. 2). В условиях установившегося баланса между процессами упрочнения и разупрочнения параметр Z выражается через гиперболический синус напряжений о m [4]:

Z =^£ exp ( Q | = A [ sinh ( «° m ) ] n . ⁽²⁾

Соответственно, сами напряжения оm определя- ются выражением о m

0,70           0,75           0,80           0,85

1000/Т

• б)

  
  
  

ln[sinh(aom)]

• в)

Рис. 3. Графическое нахождение констант а , n , A и энергии активации Q

В (2) и (3) A, а, n - константы исследуемого материала, подлежащие определению из данных экспериментов. Логарифмируя (2), получаем выражение, удобное для графического нахождения всех неизвестных параметров:

ln Z = ln e + Q— = In A + n In [ sinh( ao ) ] . (4) RT

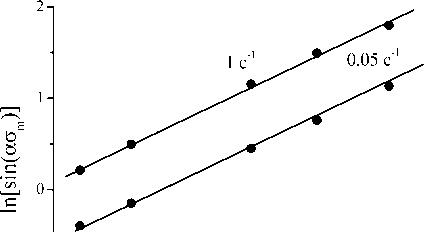
Согласно (4) зависимости ln e от ln [ sinh( ao _m ) ] в условиях постоянной температуры деформации должны иметь вид прямых линий с равным наклоном, определяющим константу n . Используя экспериментальные значения о _m , взятые из кривых течения при температурах деформации 1000 °С и 1150 °С (рис. 1, в, г), находим значение а = 0,01 МПа^-1, обеспечивающее параллельность прямых, и величину наклона n = 4,967 (рис. 3, а).

Зависимости ln [ sinh( ao _m ) ] от величины 1/ T в условиях постоянства скорости деформации также должные иметь вид прямых, наклон которых определяет энергию активации Q . Определив экспериментальные значения о _m по кривым течения при скоростях деформации 0,05 с^–1 и 1 с^–1 (рис. 1, а, б), строим соответствующие графики (рис. 3, б) и находим значение Q = 432,5 кДж/моль.

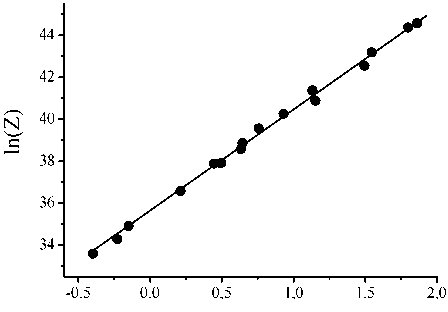
Используя полученное значение энергии активации, рассчитываем параметры Зинера – Холломона Z для всех экспериментальных режимов и строим зависимость ln( Z ) от ln [ sinh( ao _m ) ] (рис. 3, в). В полном соответствии с выражением (4) экспериментальные точки ложатся на прямую линию, что свидетельствует о применимости модели [4] для описания деформационного поведения исследуемой

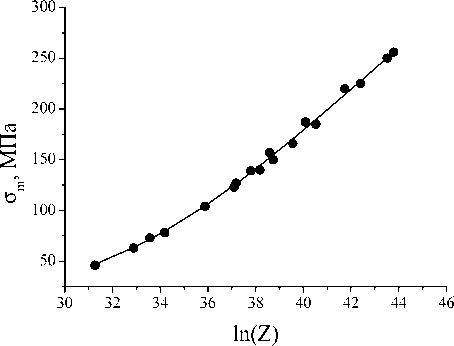
Рис. 4. Экспериментальные (точки) и расчетные (сплошная линия) значения максимальных напряжений течения в зависимости от величины параметра Зинера – Холломона

Экспериментальные и расчетные напряжения о _m в зависимости от температурно-скоростных условий горячей деформации

№ Скорость деформации, с–1 Температура деформации, °С Параметр Z omKC, МПа omac4, МПа Отклонение, % 1 0,01 1150 4,5-1013 46 47 –1,8 2 0,05 1150 2,2-1014 63 63 0,2 3 0,1 1150 4,5-1014 73 71 2,6 4 0,05 1100 8,3-1014 78 79 –1,3 5 1 1150 4,5-1015 108 104 0,3 6 0,05 1000 1,б-1016 123 125 –1,3 7 1 1100 1,7-1016 127 126 1 8 0,1 1000 3,1-1016 139 137 1,5 9 10 1150 4,5-1016 140 144 –2,5 10 1 1050 6,8-1016 157 151 3,6 11 0,05 950 8,1-1016 150 155 –3,1 12 40 1150 1,8-1017 166 170 –2,4 13 1 1000 3,1-1017 187 181 3,3 14 0,05 900 4,9-1017 185 190 –2,5 15 1 950 1,6-1018 220 214 2,7 16 10 1000 3,1-1018 225 227 –1,1 17 1 900 9,7-1018 250 251 –0,3 18 40 1000 1,3-1019 256 256 –0 стали в условиях горячей деформации. Пересечение прямой с осью ординат определяет значение последней искомой константы A = 2,1 • 1015 с-1 в выражении (2).

Оценки параметров, полученные из графического анализа, не претендуют на высокую точность, так как для определения констант материала а , n и энергии активации Q использовались ограниченные наборы экспериментальных данных. Поэтому полученные оценки были приняты в качестве начальных значений для регрессионного анализа полного набора экспериментальных данных путем минимизации невязки

S(A,n,а,Q) = ^ К" )„—(°m(A,п,а,Q))n] , (5) nn где (om^) - экспериментальное значение напря-n жений om для данного температурно-скоростного режима деформации, (om (A, n, а, Q))n - соответст- вующее значение регрессионной функции, определяемой выражением (3). Используя встроенные функции регрессии пакета Mathcad, получены следующие уточненные значения искомых параметров: а = 0,0094 МПа-1; n = 5,018; A = 2,31-1015 с-1; Q = 426,4 кДж/моль. Подставляя уточненные зна- чения параметров в (3), получаем:

o _m = 106,05 arcsinh ( 8,766 • 10 ^{- 4} Z 01" ) ,

Z = e exp

51280 T

.

Результаты расчета напряжений o _m по выражению (4) (сплошная линия) вместе с их экспериментальными значениями (точки) для разных значений параметра Z представлены на рис. 4 и в таблице. Отклонения рассчитанных значений максимальных напряжений течения от экспериментальных значений не превышает 3,5 %. При напряжениях o _m , превышающих 100 МПа, зависимость o _m от ln( Z ) с высокой точностью носит линейных характер и может быть аппроксимирована следующим выражением, удобным для инженерных расчетов:

o _m =- 602,2 + 19,47ln( Z ) =

- 602,2 + 19,47 ln( e ) +

998700 T

Как указывалось выше, параметр Зинера – Холломона определяет не только уровень напря- жений течения, но и возможность протекания процессов динамической рекристаллизации. В таблице температурно-скоростные режимы деформации расположены в порядке возрастания параметра Z. Сравнение данных таблицы с экспериментальными кривыми течения (рис. 1) показывает, что признаки динамической рекристаллизации, заключающиеся в падении напряжений течения после достижения пиковых значений, наблюдаются в первых шести режимах деформации, соответствующих значениям Z < 1,6 •Ю16 параметра Зинера -Холломона. Однако отметим, что на кривой течения, соответствующей режиму № 6 (e = 0,05, t = 1000 °C , Z = 1,6 • 1016), признаки динамической рекристаллизации выражены более отчетливо, чем на кривой течения режима № 5 (e = 1, t = 1150 °C , Z = 4,5•Ю15) с меньшим значением параметра Зинера – Холломона. Вероятно, это обстоятельство объясняется тем, что в образцах, нагретых от комнатной температуры до более низкой температуры испытания (режим № 6), формируются более мелкие зерна аустенита, что способствует протеканию процессов динамической рекристаллизации в ходе последующей горячей деформации.

Полученные в работе результаты – первый шаг в построении полной модели деформационного поведения исследуемой стали, которая позволит предсказывать вид кривых течения при заданных температурно-скоростных режимах горячей деформации.