Исследование деформационных свойств неосушенной торфяной залежи методом статистического моделирования

В течение нескольких лет проводились экспериментальные исследования проходимости машин КПО по верховой неосушенной торфяной залежи [1].

Машина КПО - машина на пневматических арочных шинах. Она непотопляема - достаточный объем и герметичность 16 арочных шин обеспечивают ее плавучесть. Арочные шины имеют диаметр 1,5м и ширину 0,84м. Вертикальная нагрузка на каждую шину составляла 12,5кН. По результатам этих исследований получена эмпирическая формула, позволяющая вычислять осадку колеса машины КПО:

Н = (0,064/-)-0,167 м,                          (1)

где 7 — сопротивление сдвигу верхнего слоя залежи, кг/ ог .

Согласно этим исследованиям прохождение колеса по верховой неосушенной залежи обеспечивается, если выполняется условие:

Н <  0 35' Г м,                            (2)

где D— диаметр колеса, м

Величина 7 на практике легко определяется с помощью сдвигомера типа СК (сдвигомер- крыльчатка). Определив с помощью СК значение 7 на любой трассе, с использованием формул (1) и (2) легко решить вопрос о возможности прохода по этой трассе машины КПО.

В связи с тем, что возможность перемещения машины КПО по тому или иному участку залежи определялась величиной сопротивления сдвигу верхнего слоя залежи на этом участке, Персиков В.И. выполнил исследования сопротивления сдвигу верхнего слоя залежи на многих месторождениях верхового типа. В результате этих исследований было установлено, что сопротивление сдвигу г верхнего слоя верховой неосушенной залежи - случайная величина. Закон распределения г был установлен по результатам 5100 измерений с большой точностью

(коэффициент вариаций дисперсии составил менее 2%). В таблице закон распределения т представлен в виде статистического ряда.

Результаты исследования. Персикова В.И непосредственно могут быть использованы только для оценки проходимости по верховой неосушенной залежи машины КПО. В общем случае при проектировании машины для решения вопроса о проходимости машины нужно знать коэффициент упругости залежи к . Причем следует учитывать, что k является случайной величиной. Следовательно, при расчёте машины на проходимость, необходимо учитывать закон распределения k . Для верховой неосушенной залежи таких данных нет, но они могут быть получены на основании экспериментальных исследований Персикова В.И.

Закон распределения т

Таблица 1

№ интервала	Границы интервала,кг/см2	Плотность распределения f ,см2/кг
1	0,02-0,04	0,538
2	0,04-0,06	1
3	0,06-0,08	1,89
4	0,08-0,10	3,68
5	0,10-0,12	6,8
6	0,12-0,14	10,6
7	0,14-0,16	10,05
8	0,16-0,18	9,4
9	0,18-0,20	3,57
10	0,20-0,22	1,68
11	0,22-0,24	0,785

Закон распределения т , полученный ПерсиковымВ.И., и может быть использован для получения закона распределения k .

В соответствии с формулой (1) каждому значению т соответствует определенное значение осадки Н колеса машины КПО. Каждому значению осадки Н соответствует определенное значение объёма V погруженной в залежь части колеса. Зная V ,коэффициент упругости залежи можно вычислить по формуле:

k=Q/V , (3) где Q – нагрузка на колесо КПО ,12,5 кН.

Таким образом , k является функцией т – случайной велечины, закон распределения которой известен. Нахождение закона распределения k в данном случае сводится к чисто математической задаче – нахождение закона распределения функции случайного аргумента [2]. Для решения этой задачи можно использовать метод статистического моделирования [3].

В основу метода положены следующие соображения. В соответствие с законом распределения т, методом обратных функций, можно смоделировать (получить) одну реализацию т. С использованием этой реализации, по формуле (1) можно вычислить осадку арочного колеса Н . По величине Н можно определить объём погруженной части колеса V . Зная V по формуле (3) находим k .

Многократно повторив описанную последовательность действий, получим статистическую совокупность значений k . Путем обычной статистической обработки статистической совокупности k можно получить закон распределения k.

Одна из задач, которую нужно решить при моделировании т– определить количество реализаций n , при котором закон распределения смоделированной совокупности реализаций будет практически не отличатся от исходного закона распределения полученного Персиковым В.И.

Для решения этой задачи была разработана компьютерная программа, позволяющая на основании закона распределения случайной величины, представленного в виде статистического ряда, моделировать любое количество реализаций этой величины. С использованием этой программы были смоделированы совокупности т с количеством реализаций 500,1000,2000,4000,6000,8000,10000.

Степень отличия закона распределения смоделированной совокупности т от исходного закона оценивалась коэффициентом вариации:

IV =--100%,                         (4)

где а — среднеквадратичное отклонение плотности распределения,

М—математическое отклонение плотности исходного статистического ряда.

Среднеквадратическое отклонение вычисляется по формуле:

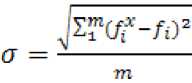
где ft — плотность распределения ,полученная в результате статистической обработки смоделированной совокупности т;

f — плотность распределения по исходному статистическому ряду;

m — количество интервалов статистического ряда. Математическое ожидание вычисляется по формуле:

м =

т

На рис.1 приведена зависимость W от n . Эта зависимость показывает, что с увеличением n коэффициент вариации уменьшается.

При n =8000…10000 коэффициент вариации практически не изменяется и находится в среднем в пределах 2%. На этом основании решено при реализации метода статистического моделирования необходимо вырабатывать 10000 значений т.

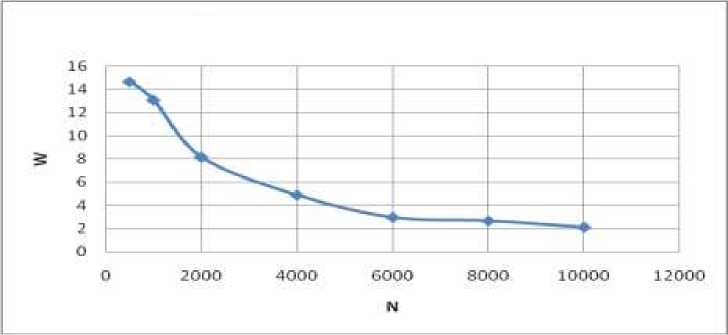
Рис. 1 Зависимость коэффициента вариации W от количества реализаций в совокупности n.

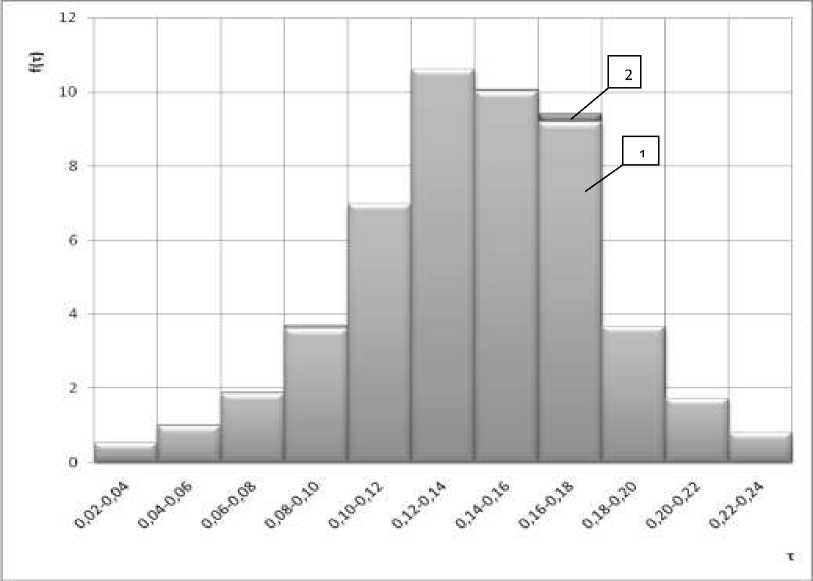
Рис. 2. Закон распределения т (гистограмма):

1- Исходный

2- Смоделированный ( при n =10000).

For research of deformation properties of the top layer not drained deposits it is offered to use the known law of distribution of resistance to shift τ top layer of these deposits and a method of statistical modeling. Computer experiments have allowed to establish that at realization of a method of statistical modeling it is necessary to develop 10000 values τ.