Исследование динамики агрегата ротационного типа

Разрабатываемый фрезерный агрегат предназначен для поверхностной обработки дорожных покрытий. В процессе его испытаний были выполнены измерения сил резания следующих материалов: асфальт и лед. Схема для однокомпонентного измерения тензометрическим датчиком (далее тензодатчик) консольного типа силы резания материалов агрегатом в ручном режиме работы представлена на рис. 1. В представленной схеме производится измерение вертикальной составляющей силы резания. Две другие составляющие силы резания: в поперечном и продольном направлении относительно перемещения агрегата измерялись при других расположениях тензодатчика, получаемых путем разворота на 90 градусов.

Рис. 1. Схема измерения вертикальной составляющей силы резания в ручном режиме работы агрегата

В ходе эксперимента оператор вручную плавно приводил в касание барабан фрезерного агрегата с обрабатываемым материалом. Практически сразу начинается разрушение материала. Выявлено, что при малом давлении барабана на обрабатываемую поверхность получаются частицы разрушенного материала малого размера. С увеличением давления на материал увеличивается вертикальная составляющая усилия N в и размеры частиц.

Результаты проведенных экспериментальных исследований процесса ротационного фрезерования в ручном режиме работы мобильного агрегата близки к результатам, полученным в лабораторных условиях на стационарном фрезерном станке [1]. Принципиальное отличие рассматриваемой схемы ротационного фрезерования в кинематической схеме и типе режущих элементов. На рис. 2 показан вариант агрегата с осью вращения водила (барабана), расположенной параллельно обрабатываемой поверхности. В статье [1] ось вращения водила расположена перпендикулярно обрабатываемой поверхности и на водиле установлены режущие элементы чашечного типа.

Рис. 2. Фото стенда для измерения вертикальной составляющей силы резания в ручном режиме работы агрегата

На основе фрезерного агрегата с ручным управлением разрабатывается механизированный агрегат с контуром управления положением фрезерного барабана относительно плоскости горизонта и подачи в направлении движения.

1.    Постановка задачи

На рис. 3 показана кинематическая схема фрезерного агрегата, содержащего дополнительно введенную раму 1, образующую с платформой 2 карданов подвес для фрезерного барабана (ФБ) 3. Задача проводимого исследования состоит в анализе структурных свойств агрегата и синтезе обратной связи, обеспечивающей требуемые динамические свойства в процессе поверхностной обработки. Угловое положение ФБ контролируется датчиками углов ДУ 2 и ДУ 3 , а поступательное перемещение с помощью датчика угла ДУ 4 в предположении о качении опорного колеса агрегата без проскальзывания. На рис. 4 представлены системы координат, связанные с деталями агрегата, и реакции в опорах барабана ( R bl , R br ) и фрез ( R fl , R fr ), контактирующих с материалом.

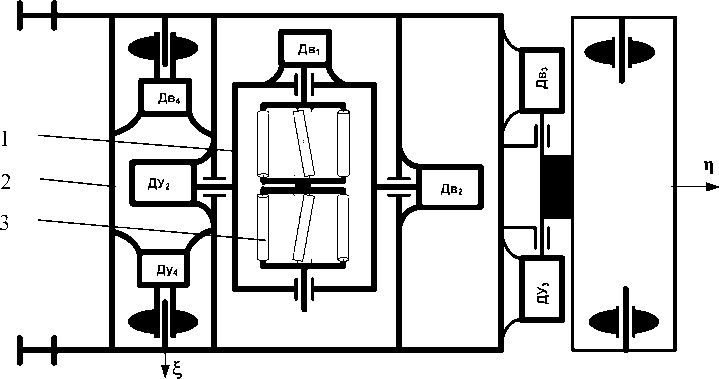
Рис. 3. Кинематическая схема агрегата

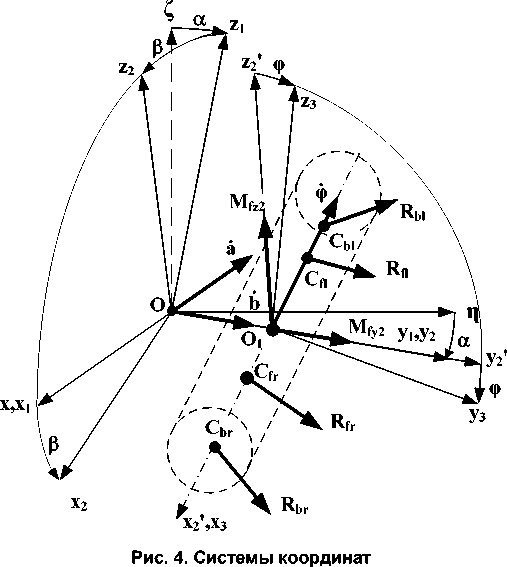
Математическая модель агрегата представлена в форме системы из дифференциальных уравнений второго порядка:

m пп-ii=Fn( t)-Rпn( t, ф, ф) ;

Jрп -a = Mдвз(t) + M(P)-Mo (ф,R,t);(2)

Jпп-в = Mдв2 (t)— mр(ф, R, t),(3)

где m _пп – суммарная масса платформы и всех установленных на ней деталей и узлов, включая массу опорного узла агрегата; р - координата поступательного перемещения платформы; F _n ( t ) - движущая сила, прикладываемая к платформе через двигатель Дв 4 ; R _{п п}( t , ф , ф ) - реакция связей агрегата с обрабатываемой поверхностью, передаваемая через узлы агрегата, выражения для которой можно представить в виде стохастической функции; M ( P ) - момент от силы тяжести платформы с ФБ относительно оси вращения рамы; M _a ( ф , R , t ) и M ^ ( ф , R , t ) - моменты от взаимодействия режущих элементов фрез с обрабатываемым материалом, выражения для которых можно представить в виде стохастической функции [2] ^R ( t , р ) = ( ^R 0 ( р ) + ^ ( t )^- о (^ ( р ) ) ) ^- Rw ( t ) , где R 0 ( р ) - реакция связи режущего элемента фрезы с обрабатываемым материалом, которая при малой подаче фрезы может быть представлена линейной функцией R 0 ( р ) = b -р + с , b , с - коэффициенты, зависящие от свойств обрабатываемого материала; Rw ( t ) = {1, для t <  t 1 и 0 для t 1 <  t <  T} - периодическая функция, модулирующая случайный процесс £ ( t ) , обусловленная вращением ФБ, несущего на себе п фрез-сателлитов; t 1 = у- п /ф , у - угловой размер фрезы-сателлита, Т = 2 л/ф - период одного оборота барабана, £ ( t ) -нормированный случайный процесс с нормальным законом распределения; дисперсия D ( A R ( х ) ) моделируемой реакции R ( t , х ) является функцией от подачи ФБ, задаваемой поступательным движением платформы в плоскости дорожного полотна: c ( A R ( х ) ) 2 = D ( A R ( х ) ) = ( kD - R 0 ( х ) ) 2 , где kD – коэффициент, зависящий от свойств обрабатываемого материала и вида фрезы; R = R ( R bi , R br , R fi , R fr ) ^.

Представим математическую модель агрегата в векторно-матричной форме Коши:

x = Ax + Bu + w (t), (4) Г X ^ в n где x = a ■ In; x – вектор Г0 0 0   l  c ap  can)     Г100 ^ 0 0 0 cpa  cpp  c         010 0 0 0 c na  cnp  c nn       001 ; A = 1  0  0   0    0    0 ; B =0  0  0 0  1  0   0    0    0          0  0  0 [0  0  1   0    0    0 )       10  0  0; состояния агрегата; А – матрица состояния; B ua ; u = up Iu n; – матриц ; w(t) = а управле Г Wa (t) ^ Wp ( t ) Wn( t ) 0 0 I 0 ; ния; u ■ – вектор управления; w (t) - вектор возмущения, обусловленный взаимодействием ротационного инстру мента с обрабатываемой поверхностью; cар, can, cра, cрр, c₽n, cna, cnp, cnn - коэффициенты, зависящие от выражений для реакций взаимодействия ротационного инструмента с обрабатываемой поверхностью; l' = 1Jрп ; l - расстояние от оси вращения фрезерного барабана до оси подвеса рамы агрегата.

Особенность построения математической модели в линейной постановке состоит в распределении коэффициентов реакций взаимодействия ротационного инструмента с обрабатываемой поверхностью на две части. В вектор возмущения w (t) вошли постоянные составляющие реакций, а через коэффициенты cар, can, cpa, cpp, cpn, cna, cnp, cnn введены линейные составляющие реакций.

Управляемость агрегата по критерию Калмана должна соответствовать выполнению следующего критерия: rank ( Q u ) = 6, где Q u = ( B A • B ... A ⁵ • B ) - матрица управляемости.

Подстановка матриц состояния A и управления B в матрицу управляемости Qu позволяет сделать вывод о выполнении критерия управляемости независимо от параметров агрегата. Для подтверждения вывода приведем подматрицу, полученную из первых двух компонент матрицы управляемости:

	Г 1 0 0 0 0 0 ^
	0 1 0 0 0 0
	0 0 1 0 0 0
Q U = ( B A • B ) =	0 0 0 1 0 0	-                                                                         (5)
	0 0 0 0 1 0
	4 0 0 0 0 0 1 ;

Находим выражение для главного определителя: |QU| = 1. Ненулевое значение главного оп- ределителя и отсутствие в его выражении параметров агрегата подтверждает структурную управляемость агрегата. Выполнение критерия управляемости дает основание сделать вывод о реализации с помощью управления u желаемых динамических свойств фрезерного агрегата.

Прямому измерению в агрегате доступны углы отклонения а и р рамы и платформы с по- мощью датчиков углов и поступательное перемещение агрегата с помощью датчика перемещения. Перечисленной совокупности датчиков соответствует следующее уравнение наблюдения:

' 0

0 10 0 ^

0 0 10

0 0 0 1 )

- матрица наблюдения; ^ ( t ) - вектор измерительного

y = Cx + § ( t ) , где C = 0 _v 0

шума Гауссова типа.

Для формирования закона управления в форме линейной комбинации переменных состояния u = P • x необходим полный вектор состояния агрегата. С помощью критерия Калмана проверим наблюдаемость агрегата с помощью матрицы наблюдаемости:

Q c = ^f C T A T • C T       ( A T ) 5 • C T ^j .

Анализ главных определителей, получаемых из матрицы наблюдаемости, позволил выбрать один, имеющий следующее численное значение:

= 1.                                                                                         (6)

Один из главных определителей матрицы наблюдаемости отличен от нуля, следовательно, rank ( Q c ) = 6 . Как и в случае с управляемостью ранг матрицы наблюдаемости не зависит от параметров агрегата, а определяется структурой его математической модели. Следовательно, можно в реальном времени восстанавливать недостающие компоненты вектора состояния агрегата и формировать управление фрезерным барабаном.

2.    Синтез обратной связи

Для формирования вектора управления u необходимо ввести регулятор размерности 3 x 6: f Р 11  - Р 16 j

P =

V ^p 31   ^{— p} 36 J

Синтез коэффициентов регулятора выполним модальным методом. С этой целью запишем характеристическое уравнение агрегата, охваченного обратной связью:

| k • E - ( A - B • P )| = 0,                                                                                (8)

где Е – единичная матрица шестого порядка.

Обозначим через V (P) вектор коэффициентов характеристического уравнения. Выражения для компонентов вектора содержат 18 неизвестных коэффициентов регулятора pij, где i = 3, j = 6 . Для нахождения численных значений коэффициентов регулятора сформируем желаемые численные значения коэффициентов характеристического уравнения. С этой целью представим передаточную функцию агрегата в виде произведения трех динамических звеньев второго порядка с различными постоянными времени Ti . Коэффициенты относительного демпфирования выберем одинаковыми со значением ^ ~ 0,7, при котором переходный процесс в агрегате будет происходить по апериодическому закону без перерегулирования. Такое требование к коэффициенту демпфирования обусловлено ожидаемым качеством результата фрезерования: исключить появление нежелательных углублений на обрабатываемой поверхности.

Обозначим через V_{λ g} вектор коэффициентов характеристического уравнения с желаемыми корнями. На основании вышеизложенного критерия назначения параметров динамических звеньев получим следующее выражение для формирования характеристического полинома с желаемыми коэффициентами:

f               j mg W = A2 + A + 72-                                      (9)

i = 1 V         T i        T i J

После раскрытия скобок и суммирования коэффициентов при различных степенях λ получим выражения для всех компонент вектора V_{λ g} .

Для нахождения коэффициентов регулятора приравняем сформированные вектора коэффициентов характеристического уравнения

V_x ( P ) = V_x g -                                                                              (10)

Для решения системы алгебраических уравнений в программе Mathcad можно воспользоваться одной из стандартных процедур find или Minerr. В систему из шести алгебраических уравнений входит 18 коэффициентов регулятора. Избыточность количества параметров регулятора можно использовать для дальнейшего улучшения свойств динамической системы. С этой целью можно сформировать дополнительные ограничения в виде равенств или неравенств, используя, например, числители передаточных функций системы. В случае возникновения проблемы в решении можно обратиться к поиску стартовой точки путем аналитического конструирования регулятора с применением матричного уравнения Риккати с матричной переменной. Решение уравнения Риккати позволяет получить регулятор, обеспечивающий устойчивость замкнутой системы. Получающиеся при этом численные значения корней могут оказаться неоптимальными по требованиям быстродействия или перерегулирования и настраиваются на следующем шаге модальным методом.

В качестве численного примера выберем следующие частоты собственных колебаний агрегата: f ₁ = 3 Гц, f ₂ = 10 Гц, f ₃ = 18 Гц, которым будут соответствовать постоянные времени: T ₁ = 0,053 с, T ₂ = 0,016 с, T ₃ = 0,009 с.

Пусть матрица состояния А имеет следующие численные значения: l ′ = 1; c _αβ = c _αη = c _βα = = c _ββ = c _βη = 0; c _ηα = c _ηβ = c _ηη = - 1 . Зададим начальные значения всех коэффициентов регулятора нулевыми p _ij = 0 , где i = 3, j = 6 . После обращения к процедуре Minerr в программе Mathcad получим значения коэффициентов регулятора (см. таблицу).

Численные значения коэффициентов регулятора

P	91,20	26,65	208,93	1170,23	–1573,16	–19014,58
	–246,91	–146,76	–2161,64	–1404,78	936,51	–16311,23
	15,31	27,86	328,25	264,05	222,27	3420,57

Подстановка коэффициентов регулятора в выражение для характеристического уравнения замкнутой системы дает следующие значения корней:

λ _1,2 = - 79,168 ± 80, 768 i ; λ _3,4 =- 43,982 ± 44,871 i ; λ _5,6 = - 13,195 ± 13,461 i .

Округление коэффициентов регулятора до целых значений с помощью функции ceil в программе Mathcad приводит к изменениям в значениях корней на величины не более 4 %, что свидетельствует о низкой чувствительности динамических свойств агрегата к изменению коэффициентов не только регулятора, но и параметров его матрицы состояния.

Реализация обратной связи в агрегате потребует восстановления всего вектора его состояния. Поскольку на агрегат поступает случайное возмущение от взаимодействия ротационного инструмента с обрабатываемым материалом, сопровождающееся измерительным шумом, то целесообразно в качестве наблюдающего устройства использовать фильтр Калмана.

Выводы

Проверка структурных свойств агрегата показывает, что на его основе можно построить дорожную фрезерную машину с требуемыми динамическими характеристиками. В качестве управляющего устройства целесообразно использовать регулятор по состоянию, коэффициенты которого можно настраивать модальным методом.