Исследование динамики асинхронного двигателя

Точное математическое описание явлений, происходящих в асинхронных машинах, сложно и громоздко, поэтому используем следующие общеизвестные допущения:

• -    отсутствие насыщения магнитной цепи;

• -    отсутствие гистерезиса;

• -    синусоидальное распределение в пространстве кривых МДС и магнитных индукций;

• -    независимость индуктивных сопротивлений рассеяния от положения ротора;

• -    полная симметрия обмоток статора.

Математическое описание асинхронного короткозамкнутого двигателя, с учtтом допущений, представим в виде систем уравнений.

Уравнения напряжений для статорной и роторной цепи соответственно имеют вид:

J

^Us 1

U s 2

^Us 3

0 =

d ^ s 1 dt

+ R_s 1

d ^ s 2 dt

d ^ s 3 dt

^d W r 1 dt

• i s 1 ,

+ R s 2

⁺ R s 3

■ z s2,

• i s 3 .

⁺ R r 1 • i r 1 ,

J o = d & 2 dt d ^r^

I ⁰ = dt

+ R r2 • i r2 ,

+ R • • i ,. r 3 r 3 .

Потокосцепление обмотки каждой фазы является функцией всех токов статора и ротора. Системы уравнений для потокосцеплений статора и ротора (соответственно индексы «s» и «r») имеют следующий вид:

V s 1 = L_s • i 1 s + ^Ls 1,2 ■ i 2 s + ^Ls 1,3 • i 3 s + ^L 1,1 • ^cos V • i r 1 + ^L 1,2 ’ C ^0S ( ^ + 2 • a ) • i r ₂ + L^ • COS( ^ + ^a ) • i_r 3 ,

’ V s 2 = L_s • i 2 s + L s 2,1 • i 1 s + L s 2,3 • i 3s + ^L 2,1 • ^COs( V + ^a ) ■ i r 1 + ^L 2,2 • ^COS V' i r 2 + ^L 2,3 • ^COs( V + ² • ^a ) ■ i r 3 , ⁽³⁾

V s 3 = ^Ls • i 3s + ^Ls 3,1 • i 1 s + ^Ls 3,2 • i 2 s + ^L 3,1 • ^COs( V + ² • ^a ) • i r 1 + ^L 3,2 • ^COs( V + ^a ) • i r 2 + ^L 3,3 • ^COS V i r 3 •

V r 1 = L r • i 1 r + L r 1,2 • i 2 r + ^Lr 1,3 • i 3r + ^L 1,1 • ^COs V • i s 1 + L 1,2 • ^COs( V + ² • ^a ) • i s 2 + ^L 1,3 • ^COs( V + ^a ) • i s 3 ,

⁽ V r 2 = ^Lr • i 2 r + ^Lr 2,1 • i 1 r + ^Lr 2,3 • i rs + ^L 2,1 • ^COs( V + ^a ) • i s 1 + ^L 2,2 • ^COs V • i s 2 + ^L 2,3 • ^COs( V + ² • ^a ) • i s 3 , ⁽⁴⁾

V _{r 3} = L_r • i_3r + L_r 3,1 • i 1 _r + L_{r 3},₂ • i ₂ r + L 3,1 • cos( v + 2 • a ) • i_s 1 + L ₃,₂ • cos( v + a ) • i_{s 2} + L ₃,₃ • cos v • i_{s 3} •

В уравнениях (3) и (4) L s и L r являются собственными индуктивностями соответствующих обмоток статора и ротора, все остальные – взаимоиндуктивностями между соответствующими обмотками статора L s1,2 , ротора L r1,2 и статора и ротора, например, L 1,1 – взаимоиндуктивность между первой обмоткой статора и первой обмоткой ротора.

В дополнение к системам уравнений (1)–(4) используем основное уравнение динамики электропривода h% = m-Mc,                         (5)

где J ^ , M, M_c, ш - соответственно суммарный момент инерции, электромагнитный и статический моменты и угловая скорость двигателя.

Момент электромагнитный может быть выражен через векторные величины потокосцепления V_rx и тока I_rx ротора в координатных осях x,y

M = V_rx х I_rx.

Несмотря на полное и строгое математическое описание, использование уравнений (1)–(6) для исследования машины встречает серьёзные трудности. Перечислим основные:

• -    в уравнениях (5)-(6) фигурируют векторные величины, а в уравнениях (1-4) скалярные;

• -    количество взаимосвязанных уравнений равно 16, а количество коэффициентов при них - 44;

• -    коэффициенты взаимоиндукции между обмотками статора и ротора в уравнениях (3) и (4) являются функцией угла поворота ротора относительно статора, то есть уравнения (3) и (4) являются уравнениями с переменными коэффициентами;

• -    уравнение (6) является нелинейным, так как в нём перемножаются переменные.

На пути упрощения математического описания асинхронной машины используем метод пространственного вектора, который позволит существенно упростить и сократить вышеприведенную систему уравнений; метод позволяет связать уравнения (1)–(6) в единую систему с векторными переменными состояниями. Суть метода состоит в том, что мгновенные значения симметричных трёхфазных переменных состояний (напряжения, токи, потокосцепления) можно математически преобразовать так, чтобы они были представлены одним пространственным вектором. Это математическое преобразование имеет вид (например, для тока статора)

^{7    2}        ’■    -2-

i = 3 ( i A ⁺ ai B ⁺ a i C ) ^,

2 п            4 п

7 JJ где a = е 3 , а = е 3 - векторы, учитывающие пространственное смещение обмоток;

i_A = I m cos a t ,

I       2 n 1                I

-

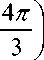
– трехфазная симметричная си-

iB = 1. cos I ° - у I, ic = I, cos I ° стема токов статора.

Приведем уравнения к безмерным (относительным) величинам. В качестве основных базовых величин выбираются амплитудные номинальные значения фазного напряжения и тока, а также номинальное значение угловой частоты иб=Ui., iб=2I111.. чб=ч = 2n f,.

На основе (8) определяются базовые значения всех переменных и коэффициентов, входящих в уравнения, а также базового времени

U      U      U3

R = Тб, L6 = -б-, We =—, Mб =-P-б-б, t6

¹б        ^ч б ¹б        ® б        ^{2    О} б

В дальнейшем используются уравнения только в относительных единицах. Обобщенная система уравнений для описания асинхронной машины примет вид:

_      _  d Ws_ us = rs • is + -7S + j • akWs, dr

_      _ , ^Ww

uR = rR -iR +   .   + j • (ak - PnU) •Wr ,dr

'             ^W S = xs • i s + x m • i R ,

Wr = xm • is + xR • iR , р = k • Mod

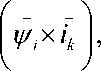
T du

J . , = P - P c • d r

В этих уравнениях все переменные относительные, полученные как результат деления реальных значений на базовые, все коэффициенты также безразмерные, полученные аналогично. Переменные и параметры в относительных единицах:

• -    u ^_ i - W

• u    = —, i = —, w =-- относительные электромагнитные переменные состояния;

U б      I б       W 6

О),         О)

• a _k = ——, u =-- относительная частота статора и относительная скорость ротора соответ-

• Об     Об

ственно;

M

• р    =-- относительный момент на валу машины;

M b

Rr    ъ L     ъ Lr SR   бS   бR r s    D , r R     n x x s     D   , x R     D , x m RбRб       Rб         Rб двигателя в относительных единицах.

2 = m m, J = E - параметры R6     V    m б

В уравнениях (10) время принято безразмерным т = — = ъб!, то есть единицей измерения време-tб ни является не секунда, а t6 =----. Следует заметить, что введение относительных величин существенно

Ъ

сокращает время моделирования и позволяет устранить многие проблемы при моделировании.

Для динамических систем необходимо учитывать переходные электромагнитные процессы в машине.

В этом случае в качестве пары переменных, описывающих машину, оставим пространственные векторы тока

■ статора и потокосцеплении ротора (iS Vr), тогда уравнения (10) после преобразования примут вид:

• ■     —-     ■ di-,-    ,        — k„ —•   . ,

us = r-is + xs~r + j ■ ak ■ xS'lS - у Vr + j • kR • Pn dr

R

—   1     ■ d ^R                     ^-

⁰ = - ^kR- r R'^lS + — 'Vr +     + + j '(a, - P n ^{v )} V r ,

T„dr

V = k-Mod(is x V-R),

T du

Jv' =~~ V - Vc • dr

где r = ( r_s + ^kR ^rs ) , x s ' = x s

x . x _ x„

— , k_R = —, T_R = — - безразмерные коэффициенты.

rR

R

В неподвижной комплексной системе координат (ъ_к = 0, a _k = 0) вещественная ось обозначается через а , а мнимая через р . Пространственные векторы в этом случае раскладываются по осям

^US   ^U S a + J^USp^ i S    i S a + j ' i S p , ^U R    ^V R a + j ' d R e , ^l R    i R a + j ' i R p ■

Система уравнений (11) в операторной форме примет вид:

u s a = ^r ■ ⁽¹ + ^T S ■ P ) ■ i S a - ^k R ■ V r a - ^k R ’ Pn ^V V r ^ ^T R

к use = r • (1 + TS ■ P) • is в - -± Vp - kR • Pn V- VRa, TR

0 = ^{- k} R • r R • i s a + — • ⁽¹ + ^T R • P ) ■ V R a + P n ^VV R e ,

I                              ^T

⁰ = - ^k R • rR • ^lS p + — ■ ⁽¹ + ^T R • P ) ■V R p + P n ^V V R a ,

^II                      ^TR

V = ^k r ■ ^V R a ■ i_S в ^- V r _P ■ i S a ),

J v' P ^U = V ^- V c ,

x где TS = —.

r

Для моделирования выберем асинхронный двигатель со следующими паспортными данными и параметрами:

PH = 14 кВт, UXh = 220 В, 11и = 27,5 А, 4 = 50 Гц, рп = 1, Rs = 0,219 Ом, R = 0,211 Ом, н          1н         1н          1н         пs            r

L s = L r = 0,094 Гн, L m = 0,092 Гн, J = 0,09 кг • м².

Значения безразмерных коэффициентов в уравнениях (12), рассчитанные по выражениям, приведенным выше, помещены в таблицу.

r	T S	K R	T R	r R	J
0,052732	2,950816	0,978723	139,8863	0,026421	153,2941

Модель АКЗ, построенная по уравнениям (12), представлена на рисунке 1.

На вход модели в момент времени т = 0 подаются напряжения u_{S a} = COS T , u S e = sin T ( a k = 1) , тем самым реализуя прямой пуск.

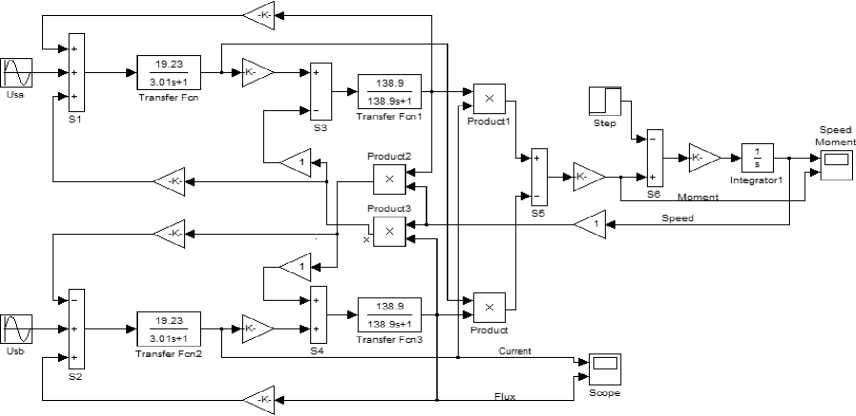
Рис. 1. Модель асинхронного короткозамкнутого двигателя

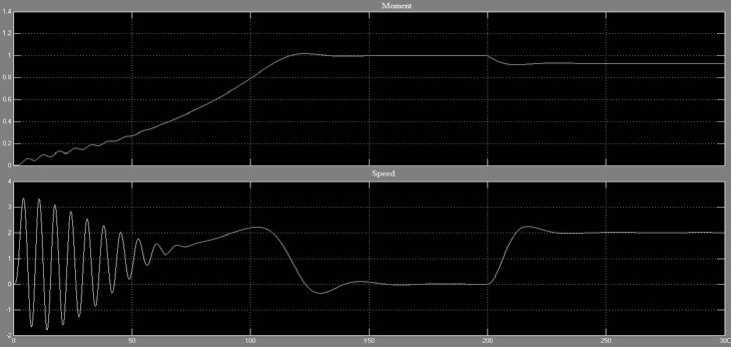
Рис. 2. Результаты моделирования асинхронного короткозамкнутого двигателя в пакете Simulink

Осциллоскопы измеряют относительные значения электромагнитного момента и скорости. Результаты моделирования представлены на рисунке 2. Они показывают, что при прямом пуске вначале наблюдаются значительные колебания момента. Такие же колебания наблюдаются в токе и скорости. Кроме того, они показывают, что при приложении момента нагрузки наблюдается уменьшение скорости.

Сравним полученную нами модель со стандартным блоком пакета Simulink Asynchronous Machine (рис. 3). Осциллограммы переходных процессов при пуске и набросе нагрузки, полученные на модели рисунка 3, представлены на рисунке 4.

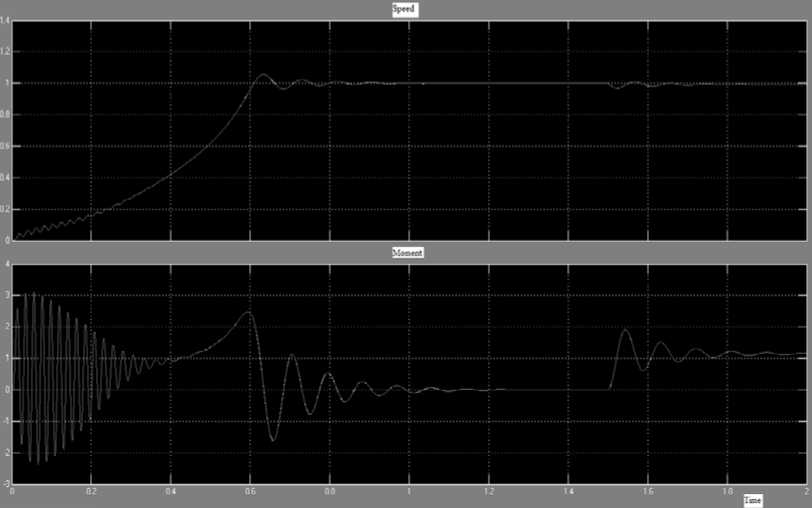
Рис. 4. Результаты моделирования

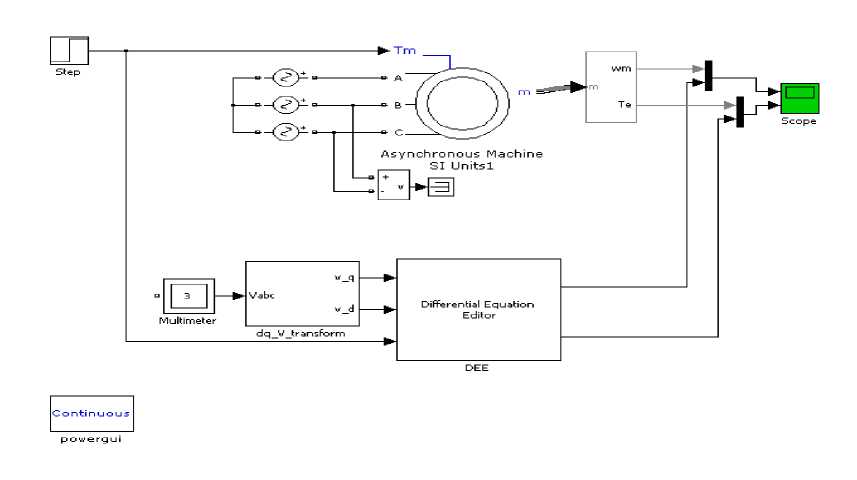
Рис.3. Модель со стандартным блоком пакета Simulink

По полученным данным делаем вывод, что созданная нами модель и стандартный блок Asynchronous Machine в пакете Simulink полностью дают идентичные переходные процессы.

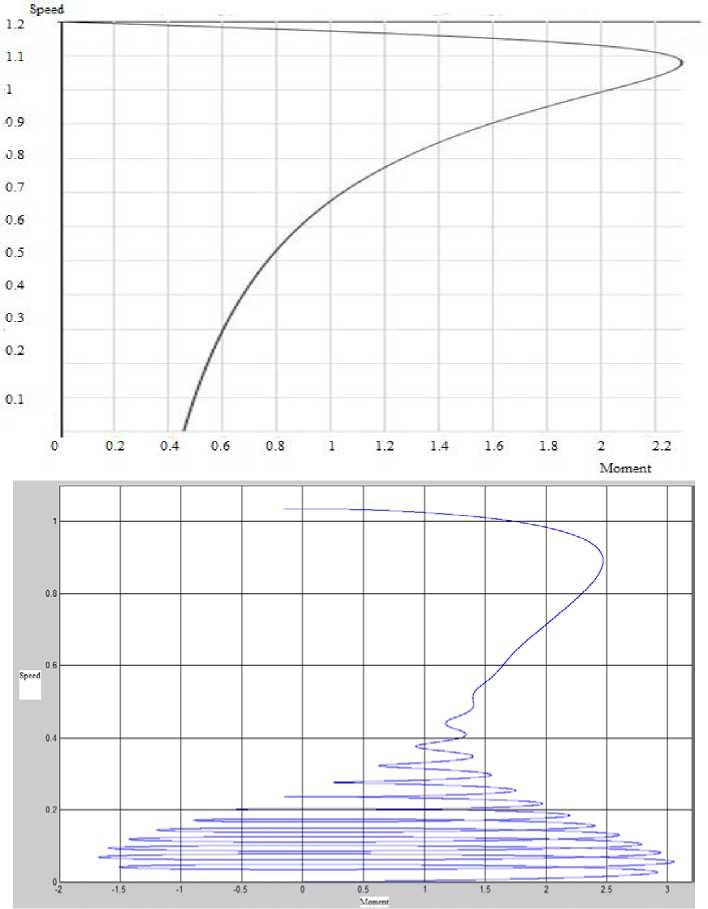
Рис. 5. Статические и динамические механические характеристики асинхронного двигателя

Как следует из осциллограмм, при пуске электромагнитный момент представляет пульсирующий характер, причём броски значительно превышают критический момент М к . Таким образом, с целью увеличения надёжности при проектировании электроприводов переменного тока, даже если не требуется регулирование скорости, необходимо учитывать, что электромагнитные моменты в пуско-тормозных режимах не только превышают критические значения, но и имеют пульсирующий характер, что может привести к выходу из строя двигателя.