Исследование динамики хирургической активности в отношении гипертензивных внутримозговых гематом с помощью математического моделирования (на примере Республики Чувашия)

и онкологических заболеваний. В структуре данной патологии кровоизлияние в мозг составляет 4-30%, возникая у 13–271 человека на 100 тыс. населения в год. Высокая частота встречаемости в популяции, крайняя дороговизна реанимационных и лечебно-реабилитационных мероприятий, обеспечения сестрин- ского, санитарного и социального ухода за больными и инвалидами обусловливают важное экономическое значение этого раздела здравоохранения [1].

Для принятия стратегических решений в области экономики здравоохранения невозможно обойтись без формирования моделей долгосрочных прогнозов, основанных на статистических данных и результатах математического анализа. Такие данные позволяют службе главного специалиста эффективно использовать бюджетные средства, разрабатывать новые и внедрять наиболее современные программные продукты с целью улучшения результатов лечения когорты больных с острым нарушением мозгового кровообращения как с медицинской, так и с экономической точки зрения [2, 3]. Математический подход не только позволяет с достоверной точностью осуществить количественное описание определенной медицинской задачи путем построения той или иной подходящей модели, но и снабжает инструментами для ее решения. Математическое моделирование, как одно из эффективных средств обоснования исследований, широко применяется в фундаментальных исследованиях [4], а также в разных областях деятельности человека: строительстве, животноводстве, медицине, образовании и экономике. Для построения прогнозов неких эпидемиологических процессов в конкретном регионе Российской Федерации обычно используют либо зарубежные математические модели, либо отечественные статистические схемы. Однако такой подход может не учитывать не только индивидуальные популяционные особенности региона, такие как плотность населения, гендерный состав, средний возраст, но и сугубо медицинские факторы, а именно плечо эвакуации, оснащенность и традиции клиники, квалификацию и опыт медицинского персонала [5, 6]. В связи с изложенным формирование индивидуальных прогностических математических моделей на основе баз данных конкретного региона может иметь важное медицинское и экономическое значение.

Цель: улучшение показателей эффективности результатов лечения больных с гипертензивными внутричерепными гематомами за счет оптимизации планирования хирургического и консервативного лечения на основе разработки математической модели эпидемиологических данных и динамики показателей хирургического лечения этих больных в Чувашской Республике.

Материал и методы. Работа основана на ретроспективном анализе 225 историй болезни пациентов с гипертензивными внутримозговыми гематомами, находившихся на обследовании и лечении в Республиканской клинической больнице города Чебоксары с января 2008 г. по декабрь 2017 г. Возраст больных варьировался от 18 до 80 лет (средний возраст 55±6 лет). Женщин было 94 (42%), мужчин 131 человек (58%). В лечении применялись как малоинвазивные, так и открытые методы хирургического лечения гематом. С помощью малоинвазивных методов оперировано 68 больных (30,2%), стандартная краниотомия использовалась у 157 человек. Летальность составила 35 человек (22,3%), способных к самообслуживанию было 77 человек (34,2%), способных вернуться к работе 47 человек (29,9%).

В качестве метода исследования выбрано математическое моделирование, позволяющее на основе статистической информации восстановить исследуемый процесс в виде математической модели и осуществлять достаточно хорошее прогнозирование ин- тересующих показателей на основе дисперсионного анализа авторской разработки [7, 8].

Первая математическая модель направлена на исследование динамики количества операций пациентов с диагнозом геморрагического инсульта. Для построения математической модели применена технология обработки аддитивной модели временного ряда:

Y=T+S+E , где Y — количество проведенных операций; T — трендовая компонента, являющаяся основной в определении количества проведенных операций; S — циклическая компонента, представляющая дополнение трендовой компоненты по количеству проведенных операций; E — случайная компонента, значение которой формируется неучтенными в процессе исследования факторами, влияющими на количество проведенных операций.

На основании расчетов по исходной информации получена трендовая компонента:

T=539,93–6,16*t, где t — временной показатель.

Доверительный интервал прогнозируемого значения рассчитан на основе дисперсионного анализа. Значимость построенной модели подтверждена статистическим критерием Фишера F _кр (1; 5; 0,05) =6,61 на уровне α=0,05; F _набл =17,55. Принимается конкурирующая гипотеза о значимости построенной математической модели H ₁ : R ²≠0. Показатель качества построенной модели, основанный на дисперсионном анализе, составляет R ²=0,77.

Вторая модель отражает динамику числа оперированных пациентов в группе 50–70 лет с 2011 по 2017 г. За основу математической модели выбрана аддитивная структура временного ряда. Трендовая компонента имеет вид:

T =19,45–0,11* t .

Значимость построенной модели подтверждена статистическим критерием Фишера F _кр (1; 6; 0,05) =5,99 на уровне значимости α=0,05; F _набл =93,45. Принимается конкурирующая гипотеза о значимости построенной математической модели H ₁ : R ²≠0. Показатель качества построенной модели, основанный на дисперсионном анализе, составляет R ²=0,93 [9].

Следующая модель представляет динамику летальности проведенного хирургического лечения гипертензивных гематом в группе больных 50–70 лет за период с 2011 по 2017 г. Для модели также выбрана аддитивная структура временного ряда:

Y=T+S+E.

Трендовая компонента представляется выражением

T =2,83+0,20* t .

Значимость построенной модели подтверждена статистическим критерием Фишера F _набл =11,81; F _кр (1; 6; 0,05) =5,99 на уровне значимости α=0,05. Принимается конкурирующая гипотеза о значимости построенной математической модели H ₁ : R ²≠0. Показатель качества построенной модели, основанный на дисперсионном анализе [10], составляет R²=0,58. Доверительный интервал прогнозируемого количества летальности при оперативном лечении получен на основе дисперсионного анализа [7, 9]:

2,05≤Y ₂₀₁₈ ≤4,98.

Результаты. Геометрическая интерпретация исходной информации количества проведенных операций и построенная модель представлены на рис. 1, где 1-й ряд соответствует исходной информации, а 2-й ряд — построенной модели. Построенная модель была протестирована на 2017 г. Доверительный интервал прогнозируемого количества операций:

385,66≤Y ₂₀₁₇ ≤521,69.

Фактическое значение на 2017 г. составило Y ₂₀₁₇ =463 операции. Трендовая компонента свидетельствует о тенденции уменьшения количества операций по диагнозу «геморрагический инсульт».

На рис. 2. представлена геометрическая интерпретация исходной информации и построенной математической модели динамики числа оперированных пациентов с гипертензивными внутричерепными гематомами: 1-й ряд соответствует исходной информации, а 2-й ряд — построенной модели. Доверительный интервал прогнозируемого результата на 2018 г.:

22,28≤Y ₂₀₁₈ ≤25,14.

Фактическое значение показателя на 2018 г. составило 24 операции.

Геометрическая интерпретация исходной информации и прогнозируемых данных математического моделирования частоты послеоперационной летальности представлена на рис. 3, где 1-й ряд соответствует исходной информации, а 2-й ряд — прогнозируемым данным.

Для сравнения приведено фактическое значение показателя Y ₂₀₁₈ =4.

Нами выявлено, что в период с 2011 по 2017 г. отмечалось сокращение количества операций по поводу гипертензивных внутримозговых гематом с 35 до 19; снижение летальности этих больных с объемом гематом от 30 до 60 мл с 2011 по 2017 г.; уменьшение количества операций в группе больных от 50 до 70 лет, у которых инсульты встречались наиболее часто, с 2010 по 2017 г.

Обсуждение. В работе построены прогностические модели показателей хирургической активности и послеоперационной летальности пациентов с гипертензивными внутримозговыми гематомами, показатели качества которых достаточно высоки. Анализ моделей и их комментарии позволяют определить порядок мероприятий, направленных на повышение эффективности оперативного лечения пациентов.

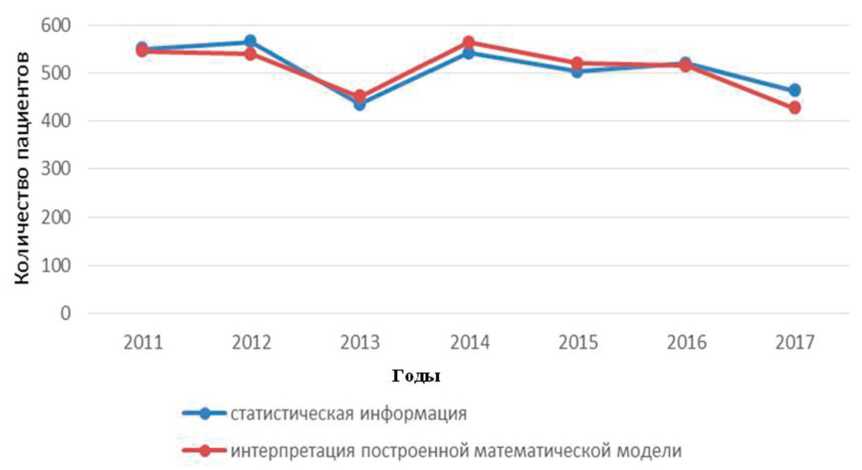
Рис. 1. Количество операций с 2011 по 2017 г.: 1-й ряд — статистическая информация по количеству операций с 2011 по 2017 г.; 2-й ряд — интерпретация построенной математической модели количества операций с 2011 по 2017 г.

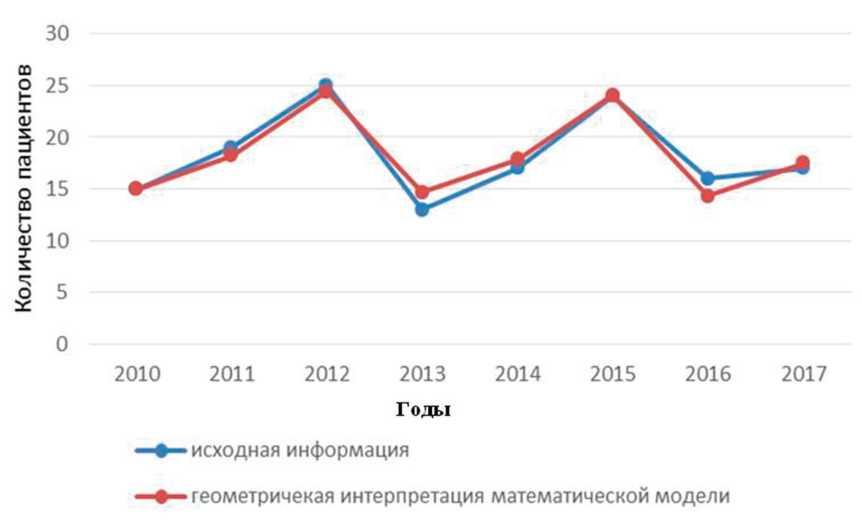
Рис. 2. Количество больных, оперированных по поводу гипертензивных гематом в возрастной категории от 50 до 70 лет за период с 2010 по 2017 г.: 1-й ряд — исходная информация; 2-й ряд — геометричекая интерпретация математической модели

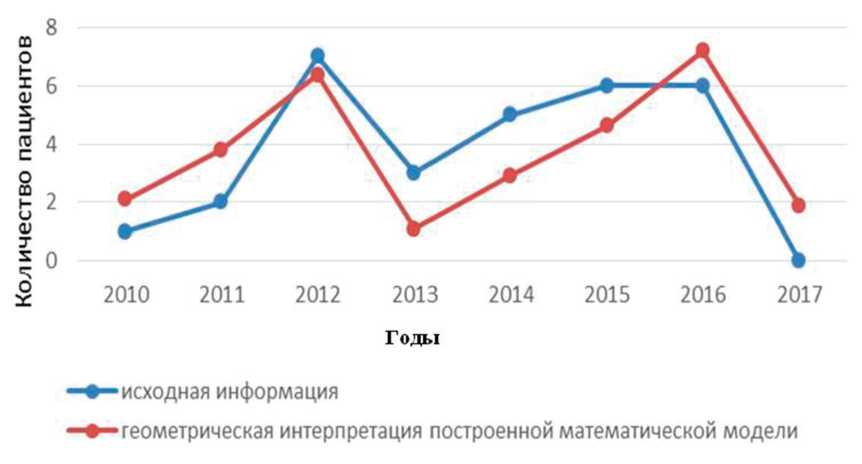
Рис. 3. Динамика летальности при хирургическом лечении гипертензивных гематом в возрастной категории 50–70 лет: 1-й ряд — исходная информация; 2-й ряд — геометрическая интерпретация построенной математической модели

Представленная в работе динамика статистических характеристик специализированной нейрохирургической помощи данной когорте пациентов, на наш взгляд, обусловлена двумя основными факторами, а именно изменениями в организационно-методической и технической составляющих лечебного процесса [10]. Первая составляющая определяет дифференцированную, основанную на индивидуальном комплексном подходе тактику лечения, как воплощение концепции персонифицированной медицины. Конечным результатом такого концептуального подхода явилось внедрение системы поддержки принятия врачебного лечения в виде балльной системы (в начале исследования) и программного обеспечения, интегрированного в электронную историю болезни в настоящее время. При этом учитываются такие признаки, как тяжесть общего состояния больного, уровень угнетения сознания, характер кровоизлияния и объем внутримозговой гематомы, состояние системы гемостаза. Это информационное обеспечение позволяет любому участвующему в лечении больного врачу ориентироваться в дальнейшей тактике ведения и проводить адекватную терапевтическую концепцию. Конечная цель такого развития: разработка и применение на практике электронной истории болезни пятого поколения по R. M. Gardner (1994) [11].

С другой стороны, следует отметить, что внедрение в повседневную хирургическую практику таких высокотехнологичных методик, как безрамная навигация, микрохирургия, нейроэндоскопия, включающая и тубулярные ретракторы, безусловно способствует снижению степени травматичности операции и, как следствие, улучшению ее исходов [12].

Внедрение на этапах диагностики, принятия решения и в ходе хирургического пособия современных медицинских технологий позволило повысить эффективность лечения больных с острым нарушением мозгового кровообращения. Математический подход, в свою очередь, помогает избежать избыточных финансовых затрат на определенных, прежде всего хирургических, этапах специализированной медицинской помощи, перераспределив их, например, на этап реабилитации.

Заключение. Адекватные статистические популяционные и медицинские когортные исследования должны проводиться с целью формирования математической модели и в конечном счете прогнозирования количества объемов оказания медицинской помощи населению по различным профилям на ближайшие годы, что реально поможет правильно оптимизировать — с точки зрения не только финансовой эффективности, но и медицинской адекватности — систему оказания специализированной медицинской помощи населению конкретного субъекта Российской Федерации.