Исследование динамики кубита во внешнем поле лазера

Теория открытых квантовых систем описывает поведение квантовой системы, взаимодействующей с внешней средой. Окружающая среда реагирует на изменения состояния системы не мгновенно, вследствие чего возникает эффект памяти. В большинстве случаев взаимодействие системы и окружающей среды достаточно слабое, поэтому эффектом памяти можно пренебречь, и, следовательно, динамику таких систем можно описать в марковском приближении [1].

В современных исследованиях встречается всё больше квантовых систем, которые не могут быть описаны посредством стандартных методов. В таких системах эффекты памяти могут играть значительную роль и динамика будет существенно немарковской. К подобным системам можно отнести микромеханиче-ские резонаторы [2], квантовые точки [3, 4], сверхпроводящие кубиты [5], источники одиночных фотонов, необходимые для квантовой коммуникации [6].

На сегодняшний день не существует общей теории немарковской динамики квантовых систем. Попытки обобщения марковского уравнения на немарковский случай приводят к появлению нефизических эффектов в решении, таких как отрицательные или большие единицы вероятности [1]. Таким вероятностям сложно придать разумный физический смысл. Альтернативой подхода на основе кинетического уравнения является подход, основанный на стохастическом уравнении Шрёдингера (СУШ) [7], который гарантированно ведёт к физическому результату для вероятностей.

Ранее в [8] рассматривалось влияние немарковской обратной связи на динамику двухуровневого атома во внешнем лазерном поле. В данной статье рассмотрена модель кубита в лазерном поле в немарковском окружении, которое описывается процессом Орнштейна–Уленбека и влияние его параметров на динамику модели. Целью статьи является выявления влияния немарковости окружения на динамику кубита.

Статья построена следующим образом: в первом параграфе строится нелинейное СУШ для немарковского случая, в параграфе два мы адаптируем нели- нейное СУШ для случая кубита во внешнем шумящем лазерном поле, в третьем параграфе обсуждаются результаты численного моделирования, и заключение содержит выводы.

1.    Стохастическое уравнение Шрёдингера

В качестве мощного инструмента для описания динамики открытых квантовых систем часто используется стохастическое уравнение Шрёдингера [7], которое для диффузионного случая имеет вид:

d y ( t ) = K ( t Ж t )d t + ^L j ( t ) y ( t - )d W j ( t ), (1)

где W j ( t ) – стандартные винеровские процессы, независимые для разных j , L j ( t ) – некоторые операторы, описывающие квантовые переходы под действием шума, K ( t ) – некоторый оператор, описывающий регулярную составляющую релаксации. Для возможности придать членам данного уравнения физический смысл необходимо, чтобы квадрат нормы волновой функции ||v ( t )|| = ^ w ( t )| V ( t )} сохранял своё значение в среднем E[|| ^ (t)||²]=1, т.е. необходимо, чтобы норма была мартингалом [7]. Данное требование налагает ограничение на структуру оператора K ( t ):

K (t) = - iH (t) -1 ^ L (t) Lj( t), (2) 2j где H(t) – эрмитов оператор, гамильтониан системы. Известно [1], что марковское СУШ (1) всегда соответствует некоторому марковскому кинетическому уравнению. Для обобщения марковского СУШ на немарковский случай в работе [8] было предложено заменить винеровский белый шум на более общий немарковский процесс. Полученное таким образом уравнение позволяет описывать случайную динамику системы в немарковском приближении.

При замене винеровского процесса более общим процессом Орнштейна–Уленбека, задаваемым уравнением:

dX j (t ) = - k_jX_j(.t )d t + d W j ( t ), k j > 0, (3)

уравнение (1) примет вид:

N( t ) = K ( t ) v ( t - )d t + X L ( t M t - )dX j (t ),      (4)

которое можно переписать:

N( t ) = I K ( t ) - X k j L j ( t ) X j ( t ) L( t — )d t +

I j J (5)

+ X L j ( t ) _V ( t - )d W j ( t ).

Условие сохранения свойств мартингала в таком

случае эквивалентно следующему условию:

K ( t ) + K ^j ( t ) - X k j X j ( t ) ( L j ( t ) + L ( t ) ) + + X L ( t ) L j ( t ) = 0,

которое должно выполняться для произвольного момента времени.

Для того чтобы условие (6) выполнялась гарантированно для любых t , необходимо, чтобы член с X j ( t ) был равен нулю. Для этого можно потребовать либо антиэрмитовость оператора L j ( t ), либо представить оператор K ( t ) в виде:

K ( t ) = - iH ( t ) + X k j X j ( t ) L j ( t ) - 1 X L j ( t ) L j ( t ). (7) j                        2 j

Чтобы придать физической смысл прибавке в виде суммы X kjXj (t)Lj (t), можно провести замену опе раторов Lj (t) на iLj (t), не меняющую средних значений наблюдаемых, тогда немарковское СУШ принимает вид:

d v ( t ) = I - i"H ( t ) + ¹ X L ( t ) L j ( t ) L( t - )d t +

^{V 2} j )                  (8)

+i XLj(t t Ж t- )d Wj( t), где Hˆ (t) – гамильтониан, модифицированный дополнительным внешним полем, скоррелированным с окружающей средой:

H ( t ) = H ( t ) + X j L j ( t ) + L ( t ) ) X j ( t ).         (9)

Уравнение (8) со случайным гамильтонианом (9) представляет собой линейное СУШ для немарковского случая, гарантированно сохраняющее среднее значение нормы волновой функции.

Переход к нелинейному уравнению

С точки зрения численного моделирования линейное стохастическое уравнение Шрёдингера является неудобным из-за огромной дисперсии стохастических траекторий. Данная проблема решается заменой волновой функции ^ ( t ), удовлетворяющей уравнению (8), на нормированную волновую функцию \pr ( t ) = v ( t ) / ||v( t )|| и построением уравнения для последней. Новое уравнение называется нелинейным

стохастическим уравнением Шредингера [7] и имеет вид

d y ( t ) = K ( t ) y ( t - )d t +

E l             1      . I

I iLj(t) "T mj( t) |'И(t-)d W/j( t), j V         2      )

где

Ki ( t ) = - i 7 H ( t ) -

• ^- 1 x f L j ⁽ t ) ^- \mjit t ) | L j ⁽ t ) ^- 1 X m j ^{2 (} t ),

• ² j V ²       )         ⁸ j

m j ( t ) = i ( V ( t ) | L j ( t ) - L j ( t )| y ( t^

Случайный процесс X_j ( t ) в новом пространстве будет иметь вид:

dz X j ( t ) = - k j X j ( t )d t + d W j ( t ) + m j ( t )d t ,          (13)

где винеровский процесс W_j ( t ) имеет вид:

d W j ( t ) = d W j ( t ) - m j ( t ) d t .                         (14)

Преобразование (14) носит название преобразования Гирсанова вероятностных мер [9]. Может быть показано, что новый процесс W j ( t ) является броуновским движением относительно новой вероятностной меры.

Уравнение (10) является эквивалентным линейному уравнению (8) в том смысле, что средние значения, построенные с помощью решений обоих уравнений, совпадают [7].

2. Кубит во внешнем поле

Рассмотрим кубит, помещённый в шумящее лазерное поле. Кубит представляет собой двухуровневую систему, гамильтониан которой во внешнем лазерном поле имеет вид:

H ( t ) = H о + H f ( t ),

здесь

H о = ² 2 c _z ,

^H f ⁽ t ) = f ⁽ t ) ст - + f ⁽ t ) o₊ ,

где v ₀ - частота перехода атома, a + , c , c z - матрицы Паули, f ( t ) – внешнее поле, которое можно описать формулой:

f ( t ) = ^ 2R-e ^{- i (v} t ^{+ k} о B o ⁽ t ) ) ,

где Q _R - частота Раби, v - частота лазера, B ₀( t ) - стохастический процесс Винера, представляющий собственный шум лазера и k 0 положительный параметр.

Единственный оператор при инкременте случайного процесса в уравнении (8) для данной модели будет иметь вид:

L ( t ) = V7c - , (18)

где у > 0 - скорость релаксации кубита.

3.    Результаты моделирования

Численное моделирование осуществлялось с помощью библиотеки NumPy языка Python 3.6.5. Использовалась схема Рунге–Кутта четвёртого порядка, адаптированная для СУШ [1], которая для уравнения dv( t) = A (t)v( t) dt + B (t )v( t) dW (t)

будет иметь вид:

v к + 1 =v к + 1 ( v k + 2 v k + 2 v k +v k ) a t + 6 + B ( t k ) V к ^ W k ,	(19)
v k = A ( t k ) v к ,	(20)
V k = A ( t k + 2 a t ) ^V к + 2 a t v k ,	(21)
v k = A ( t k + 2 a t ) ^v к + 2 a t v k ,	(22)
V к = A ( t k +a t ) ( v к +a t V 3 ) .	(23)

Решением уравнения является волновая функция кубита. Среднее значение произвольного оператора находится с помощью стохастического усреднения по формуле

1 ^N

(A ⁽ t )) = IF E V / ⁽ t ) A V / ⁽ t),                        ⁽²⁴⁾

N

• V / -( t ) — реализация случайной траектории.

Стандартная ошибка моделирования определяется по формуле:

N

^c ( t ) =V ^ 41 ^ — 1 ) E ( v * ( t ) A ² v - ( t )4 A ) .     (25)

Вероятность нахождения его в возбуждённом состоянии определяется средним значением следующего оператора:

p_H(t) = (o₊O-) .                                     (26)

На рис. 1 изображены вероятности обнаружить кубит в возбужденном состоянии для марковского случая (сплошная линия) и для немарковского случая с параметрами шума k = 1 (штриховая линия) и k = 2 (пунктирная линия). Результат для марковского случая получен из решения кинетического уравнения, которое можно найти в [1], для немарковского случая проводилось усреднение по 10000 траекторий. Ошибка не отмечена на графиках, поскольку не превышает толщины линии графика. Значения параметров v 0 , v , Q _R указаны в единицах параметра у .

Как можно видеть, стационарные состояния для k = 1 и k = 2 отличаются от марковского случая на величину 0,05 и 0,1 соответственно, что показывает, насколько сильное влияние немарковость оказывает на динамику системы при заданных параметрах. Кроме того, можно заметить небольшое увеличение частоты основных осцилляций и появление новых гармоник в динамике. Таким образом, можно заключить, что немарковость окружения может оказывать заметное влияние на динамику кубита.

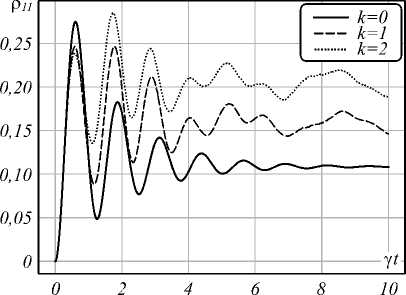
Рис. 1. Вероятности обнаружить кубит в возбуждённом состоянии в отсутствие шума лазера.

Параметры у = 1, v o = 3, v = 7, Q r = 3, к о = 0

Не менее интересным является изучение влияния собственного шума лазера на динамику системы в её немарковском окружении. На рис. 2 изображены вероятности обнаружить кубит в возбужденном состоянии для немарковского случая при наличии шума лазера с различными параметрами: k 0 = 0 (сплошная линия), k 0 = 0,3 (штриховая линия), k 0 = 0,5 (пунктирная линия), k 0 = 1 (штрихпунктирная линия). Каждый график построен усреднением по 10000 траекторий.

Как можно видеть, уже небольшое присутствие собственного шума лазера ( k 0 = 0,3) качественно влияет на динамику: увеличивается скорость релаксации, смещается стационарное состояние, а при k 0 = 1 динамика системы значительно отличается от случая без собственного шума. Можно заключить, что в данном случае собственный шум лазера уменьшает отстройку регулярной компоненты частоты лазерного поля от собственной частоты перехода кубита.

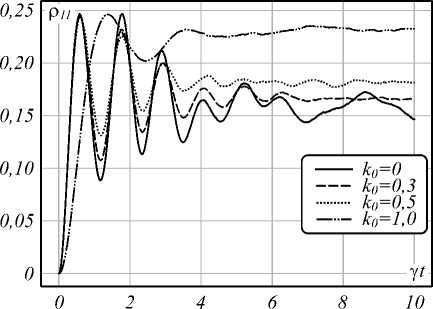
Рис. 2. Вероятности обнаружить кубит в возбужденном состоянии при различных параметрах шума лазера.

Параметры у = 1, v o = 3, v = 7, Q r = 3, к = 1

Заключение

В данной работе была исследована динамика кубита во внешнем лазерном поле с шумом. Для данной модели построено нелинейное стохастическое уравнение Шредингера, гарантирующее сохранение нормировки волнового вектора, а также отсутствие нефизических вероятностей. Влияние немарковости окружения учитывалось путем введения в уравнение процесса Орнштейна–Уленбека. При этом построенное

СУШ (8) при k =0 переходит в известное марковское уравнение Шредингера (1).

Проведено моделирование динамики кубита путём численного решения полученного нелинейного стохастического уравнение Шредингера методом Рунге–Кутты. Получены результаты в виде временных зависимостей вероятности обнаружения кубита в возбуждённом состоянии для различной степени влияния немарковского окружения на кубит, а также исследовано влияние случайного сдвига частоты лазера на динамику системы. Из анализа вероятностей показано, что стохастические компоненты лазерного поля, а также немарковость окружения могут оказывать значительное влияние на динамику.

Работа выполнена при финансовой поддержке РФФИ (грант №18-32-00249\18).