Исследование динамики лазерного излучения в зависимости от температуры в вертикально излучающих полупроводниковых лазерах

Полупроводниковые лазеры с вертикальным резонатором имеют ряд важных преимуществ по сравнению с полупроводниковыми лазерами классической полосковой геометрии: они обладают низким пороговым значением тока накачки, работают на единственной продольной моде, технологически легко формируются массивы из таких лазеров. Вертикально излучающие полупроводниковые лазеры активно применяются в беспроводных и оптоволоконных оптических системах связи, в оптических запоминающих устройствах, оптических сенсорах. Для применения полупроводниковых вертикально излучающих лазеров (ВИЛ) в таких областях, как обработка материалов, в медицинских приложениях и в качестве источников оптической накачки, необходимо увеличение выходной мощности устройства. Важной конструктивной особенностью ВИЛ является небольшой продольный размер активной среды лазера – порядка оптической длины волны, в связи с этим наиболее эффективным методом увеличения мощности ВИЛ является увеличение его поперечных размеров.

Экспериментально установлено, что поперечные размеры ВИЛ оказывают большое влияние на пространственно-временную динамику лазера и на когерентные свойства его излучения [1]. Как правило, ВИЛ с небольшими поперечными размерами (3 × 3 мкм) работает на фундаментальной поперечной моде, и характерная мощность излучения составляет порядка нескольких мВт. Увеличение мощности в ВИЛ осуществляется за счёт увеличения поперечного сечения активной области. Для поперечных размеров от 3 до 15 мкм наблюдается генерация нескольких поперечных резонаторных мод. При дальнейшем увеличении поперечных размеров в ближнем поле наблюдаются асимметричные распределения поля, которые не могут быть описаны как суперпозиция конечного числа мод пустого резонатора. Возможно по- явление нестационарных оптических структур (солитоны [2], оптические вихри [3], спиральные волны [4]) и пространственно-временной хаос.

Для получения высокой выходной мощности необходимо использование высоких инжекционных токов, приводящих к значительному разогреву активной среды лазера. В связи с этим для поддержания постоянной температуры кристалла необходимо применение охлаждающих устройств, что делает вопрос о влиянии температуры активной среды широкоапертурного полупроводникового лазера актуальным как с прикладной, так и с фундаментальной точек зрения.

Проведённые эксперименты показали, что температура кристалла влияет в первую очередь на отстройку частоты генерации от частоты продольной моды [5– 10], причём при комнатных температурах и выше отстройка частоты отрицательная, при охлаждении кристалла – отстройка положительная. Сдвиг длины волны при изменении температуры обусловлен совместным влиянием двух факторов: термического расширения активной среды и изменения показателя преломления активной среды с изменением температуры. Для устройств с круглой и квадратной апертурами при высоких температурах наблюдается преимущественно приосевая генерация. Неустойчивость режима приосевой генерации может приводить к появлению в дальнем поле множества дополнительных максимумов, расположенных вблизи центрального наиболее яркого пика. Качественно другое поведение широкоапертурного полупроводникового лазера наблюдается при достаточно сильном охлаждении устройства. В дальнем поле наблюдается множество максимумов, образующих кольцо, причём экспериментально установлено, что радиус кольца пропорционален корню из отстройки. С ростом отстройки, а также на квадратных апертурах более характерным становится наблюдение в дальнем поле четырёх ярко выраженных максимумов.

В настоящей работе показано, что модель Максвелла–Блоха качественно описывает наблюдаемую экспериментально смену режимов генерации от осевой к существенно внеосевой при изменении температуры лазерной среды.

Математическая модель

Двумерная система уравнений Максвелла–Блоха имеет вид:

( д E/ дт ) = ia A E + о ( P - E ) , <  ( д Pj дт ) = - ( 1 + i 8 ) P + DE ,

. дт

-

■ Y [ ^{D -} r ⁺ 2 ( ^E'^{P + EP} ') ,

где E , P – безразмерные комплексные огибающие электрического поля и поляризации соответственно, D - инверсия; A_± = д ² /д x ² + д ² /д y ² - двумерный Лапласиан, x , y – безразмерные поперечные координаты; Y = 7 ц / Y_± и о = к / y_± , где к , y ± и 7 ц — скорости релаксации поля, поляризации и инверсии населённости соответственно; 8 = ( to ₂₁ -to )/ Y_± — отстройка между центром линии усиления и частотой генерации, обез-размеренная на полуширину линии; a = c ² / (2 toY_± d ² ) – дифракционный параметр, где d – характерный пространственный размер в поперечном сечении пучка; r – накачка, нормированная на пороговое значение. В модели предполагается, что лазер работает на единственной продольной моде, активная среда – двухуровневая с однородно уширенной линией.

Система Максвелла–Блоха хорошо подходит для моделирования ВИЛ, поскольку принятые приближения хорошо согласуются с конструкционными особенностями ВИЛ. Продольные размеры активной области составляют порядка единиц мкм, поэтому генерация осуществляется на одной продольной моде. Усиление за проход в таком резонаторе оказывается небольшим. Основные переменные в системе за проход в резонаторе меняются слабо, что позволяет исключить из рассмотрения продольную координату z . Поперечные размеры активной области, как правило, в несколько раз больше продольных, что обеспечивает возбуждение сразу множества поперечных мод.

Метод численного моделирования

Двумерное интегрирование проводилось с помощью псевдоспектрального Фурье-метода с рас-

ˆ

ˆ

щеплением на линейный ( D ) и нелинейный ( N ) операторы (split-step Fourier method), которые можно рассматривать независимыми на малом временном промежутке dt [11]:

ˆˆ

(д U /д t) = (D + N )U,

где U =

( E )

P

D

V7

( ia A

N =

DE

-Y/ 2 (EP* + E * P) ^

Использование данного метода даёт значительное

преимущество по сравнению с конечно-разностными методами благодаря использованию быстрого преобразования Фурье. Использование симметричной формы экспоненциальных операторов обеспечивает погрешность метода порядка O ( dt ³) [11]. Решение системы (2) записывается в следующем виде:

U ( x , y , t ₀ + dt ) = exp( dt /2 • D ) x

x exp

1 0 + dt

J N t ') dt '

t ₀

• exp( dt / 2 • D ) • U ( x , y , t ₀ ).

Действие линейного оператора производится в Фурье-пространстве для основных переменных:

U ( x , y , 1 ₀ + dt /2) =

= F ¹ { exp ( dt /2 • DD k ) • F { U ( x , y , t ) } } ,

где F{..} и F-1{..} – прямое и обратное Фурье-

преобразование соответственно, k – пространственная

частота. Сама экспонента будет иметь вид:

exp ( dt /² • I ) _t ) =

( W

V

z •[ Q - W ]

Q

0         ,(5)

exp (-Y-dt/2) ^

где Z= о /( о + iak ²-1- i 8 ) , W = exp(( o + iak ²)^x dt /2) , Q = exp ( - (1 + i 8 ) • dt /2 ) - вспомогательные выражения.

Нахождение интеграла с нелинейным оператором выполняется приближенно по правилу трапеций на малом временном шаге dt в сходящемся итерационном цикле. Действие экспоненты описано ниже:

exp

t ₀ + dt

J     N /( t ') dt '

t ₀

, D =

V

1 ±

о

о

0 )

-I

(1 + i 8 )   0 ,

-Y )

• U ( x , y , 1 ₀ + dt /2) =

= U ( x , y , 1 ₀ + dt / 2) + dt /2 x

x

[ D 0 E 0 + f)Ё ]

Y^I 2r-1,2 E0P0*+ E0*P0 + EP

'* +

E * P

V

,

где E ₀, P ₀, D ₀ – величины с известного временного слоя при t = t 0 , E , P , D – переменные со слоя при t = t 0 + dt , в первом приближении равные E 0 , P 0 , D 0 соответственно. Внутри итерационного процесса также происходит действие второго линейного оператора на второй части временного шага аналогично тому, как это было на первом этапе по формулам (4) и (5). В итоге будут найдены значения E , P , D при t = t ₀+ dt , которые будут использоваться в качестве E , P , D в (6) на следующем витке итерационного цикла, и т.д.

Критерием остановки итерационного процесса является малая разница (например, = 10^–10) по норме ( L _∞ ) между получаемыми решениями E , P , D в последовательных итерациях.

Параметры в лазерной модели были выбраны близкими к реальным параметрам [9], которые характерны для ВИЛ γ = 10^–3, σ = 10^–1, r = 1..4, a = 10^–4, δ = –3..+5. Моделирование проводилось на двух формах апертур : круглой и квадратной. Форма апертуры задавалась с помощью двумерных пространственных стационарных по времени распределений параметра накачки r ( x, y ) и параметра потерь в резонаторе σ ( x, y ). По краям расчётной области располагалась поглощающая буферная зона с нулевой накачкой и очень высокими оптическими потерями, а по центру – активная область в заданной форме (круг или квадр ат). Вследствие наличия поглощающей буферной зоны за пределами активной области излучение быстро затухает . Поскольку для моделирования структур сама буферная зона является неинформативной, её размер должен быть минимальным, но достаточным для исключения взаимодействия периодов. Таким образом , апертура конечных размеров на расчётной сетке с периодическими граничными условиями моделируется исключительно параметрически. В качестве начального условия было использовано шумовое распределение вблизи состояния отсутствия генерации.

Параметры расчётной сетки были выбраны из соображений обеспечения корректного пространственного и временного разрешения моделируемых структур. При указанном выше наборе параметров возникают структуры с характерными волновыми числами k ≈ 0..200. Была выбрана пространственная сетка размером 256 ×256 и шагом dx = dy = 1/256. Она позволяет разрешать поперечные структуры с волновыми числами не более k _max = ( π / dx ) = 256 π ≈ 800, что достаточно для моделирования пространственных неоднородностей при выбранных параметрах. Выбранный шаг по времени dt = 10^–2 обеспечивает более чем достаточное временное разрешение ( ω max = 100 π ≈ 300), поскольку для характерных временных осцилляций при выбранных параметрах ω ≈ 0..5.

Результаты моделирования и обсуждение

Результаты численного моделирования распределений стационарной интенсивности в ближней и дальней зоне на прямоугольной и круглой апертурах при r = 1,5 приведены на рис. 1 и 2 соответственно.

При температурах выше 0 ⁰С ( δ ≤ 0) пороговая накачка для появления лазерной генерации зависит от величины отстройки [12, 13]:

r_thr = 1 +δ ²/(1 +σ ) ² . (7)

Вблизи порога ближнее поле широкоапертурного лазера однородно (рис. 1, 2 δ = –0,75, r = 1,5). При уменьшении абсолютной величины отстройки (рис. 1, 2 δ = 0..–0,5) в ближней зоне возникают достаточно крупные квазистационарные структуры, представляющие собой подвижные яркие пики интенсивности (волны интенсивности или филаменты) (рис. 1, 2 δ = 0..–0,5), появление которых было предсказано в работах [14 – 16]. Излучение в дальней зоне при этом имеет вид небольших размытых пятен вблизи оптической оси резонатора.

δ =–0,75

δ =–0,5

δ =0

δ =0,5

δ =1,0

δ =1,5

δ =2,0

Рис. 1. Распределения интенсивности в ближнем (слева) и дальнем поле (справа) на квадратной апертуре при r = 1,5, диапазон температур +60..-40 oC (сверху вниз)

При положительных отстройках, как показано в [12, 13], система уравнений (1) имеет простейшее решение вида бегущей волны:

E (t, r) = E0 exp (i (k± r + Q t)),

P ( t , r ) = P 0 exp ( i ( к _± r +Q t ) ) ,                      (8)

D (t, r ) = Do, где r - радиус-вектор в поперечной плоскости, | Eo|2 = r -1, Dо = 1, Po = Eo, Q = -8 , k_2 = k02 = 3/a.                                        (9)

8 =-0,75

S =-0,5

8 =0

8 = 0,5

8 =1,0

8 =1,5

8 = 2,0

Рис. 2. Распределения интенсивности в ближнем (слева) и дальнем поле (справа) на круглой апертуре при r= 1,5, диапазон температур +60..-40 oC (сверху вниз)

Физически решение (8, 9) соответствует внеосевой генерации плоской волны под углом к оси резонато- ра. То есть у волнового вектора электромагнитной волны появляется небольшая (по сравнению с продольной) поперечная составляющая k± . Пороговое условие генерации таких волн не зависит от величины положительной отстройки и соответствует rthr = 1.

Проведённое численное моделирование системы (1) подтвердило эволюционную устойчивость подобного внеосевого излучения и формируемых в результате нелинейного взаимодействия этих волн паттернов.

При 0 < 8 < 1 (соответствующая температура активной среды лежит в диапазоне 0..-20 °С [5, 9]) распределение в дальней зоне на круглой апертуре имеет форму кольца, радиус которого меняется в соответствие с (9) (рис. 1, 2 8 = 0.. 1 ). С увеличением накачки это кольцо может деформироваться и претерпевать разрывы. При этом в ближней зоне наблюдаются модулированные по пространству нестационарные оптические структуры (roll-patterns).

На прямоугольной апертуре сначала тоже образуется квазистационарное кольцо в дальней зоне, которое затем сменяется стационарным распределением в виде четырёх точек, расположенных по вершинам квадрата, вписанного в это кольцо. Это свидетельствует о преимущественном распространении четырёх поперечных наклонных (внеосевых) волн в резонаторе (рис. 1 8 = 0.. 2 ).

При температурах ниже -20 ⁰С ( 8> 1) в ближнем поле наблюдаются мелкомасштабные структуры с характерными размерами ~ k ^- 1 . Причём при d >2 в дальней зоне распределение интенсивности представляет собой четыре пика, расположенных по вершинам квадрата, и на квадратной, и на круглой апертуре.

Кроме наблюдения сценария развития динамики ВИЛ при изменении температуры, аналогично тому, что описан в экспериментальных исследованиях [510], было необходимо проверить количественное соответствие характеристик получаемых структур теоретически предсказанным.

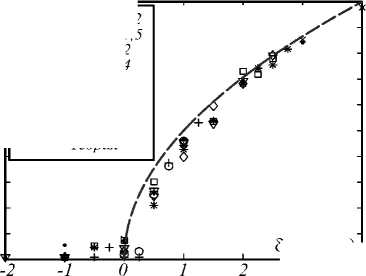
На рис. 3 представлена зависимость получаемых в дальней зоне пространственных частот от частотной отстройки. Прерывистой линией проведена теоретическая кривая (9). Маркерами нанесены точки, соответствующие различным накачкам на квадратной и круглой апертурах. Видно, что накачка и форма активной области слабо влияет на характерный пространственный спектр.

Заключение

В работе рассмотрена модель широкоапертурного полупроводникового вертикально излучающего лазера с круглой и квадратной формами апертур на основе полной системы уравнений Максвелла–Блоха в двумерном приближении. Продемонстрировано , что с помощью принятой модели может быть качественно воспроизведена экспериментально наблюдаемая смена режимов генерации от приосевой к существенно внеосевой при изменении температуры лазерной среды в ВИЛ.

Квадрат г=4 Круг г=1,2 Круг г=1,5 Круг г=2 Круг г=4

---Теория

На основе проведённого численного моделирования определена зависимость поперечной составляющей волнового числа от частотной отстройки и параметра накачки.

• к, отн. ед.

200 180 160 140 120 100 80 60 40 20 О

О Квадрат г=1,2 □ Квадрат г=1,5 х Квадрат г=2

*

О

8, отн. ед.

Рис. 3. Зависимость поперечной составляющей волнового числа от частотной отстройки для различных накачек на круглой и квадратной апертурах

Показано, что как для случая круглой апертуры, так и для случая квадратной апертуры при положительных частотных отстройках, которые соответствуют температурам ниже 0 0С, и в широком диапазоне накачек выше порога характерно внеосевое излучение. В ближней зоне при таких температурах наблюдаются промодулиро-ванные по пространству мелкомасштабные оптические структуры, в дальней зоне – излучение в виде кольца или четырёх ярких точек, лежащих на этом кольце. Радиус кольца увеличивается с отстройкой частоты (на эксперименте это соответствует дальнейшему охлаждению среды) пропорционально корню квадратному от отстройки. Напротив, при отрицательных отстройках (температурах выше 0 0С) и накачках вблизи порога наблюдается стационарный квазиоднородный режим излучения. При больших накачках получены нестационарные крупномасштабные оптические структуры. В пространственном спектре это выражается в несколько увеличенной расходимости при общем сохранении при-осевого характера излучения.

Полученное качественное соответствие построенных паттернов экспериментально наблюдаемым подтверждает применимость модели Максвелла–Блоха для теоретического исследования закономерностей формирования пространственно-временных структур в широкоапертурных ВИЛ.

Работа частично поддержана Минобрнауки РФ в рамках Программы повышения конкурентоспособности СГАУ на 2013–2020 гг. и Государственного задания вузам и научным организациям в сфере научной деятельности, проект 1451, НИР №ГР 114091840046, грантом РФФИ 14-02-31419 мол_a.