Исследование динамики процесса кручения пряжи в пневмомеханическом прядении при использовании неподвижного вьюрка ложного кручения

Введение. Известная особенность пряжи пневмомеханического прядения, заключающаяся в высоких коэффициентах крутки по сравнению с пряжей кольцевого прядения, обусловленная особенностью структуры пряжи пневмомеханического прядения и условиями ее формирования, весьма усугубляет проблему повышения потребляемой формировочнокрутильного устройства (ФКУ) мощности. Это в свою очередь делает актуальной проблему снижения коэффициента крутки пряжи пневмомеханического прядения, решение которой дало бы дополнительную возможность достижения увеличения скорости формирования пряжи в пневмомеханических прядильных машинах без увеличения частоты вращения ФКУ при соответственном снижении расхода электроэнергии [1,2,3].

Увеличение рабочих скоростей делает актуальным также вопрос изучения динамики ФКУ при кручении пряжи в новых способах получения пряжи, в частности в пневмомеханическом прядении в неустановившемся режиме во время пуска и останова.

Основная часть. Известны исследования, указывающие на перспективность применения вьюрков ложного кручения в пневмомеханическом прядении. В связи с этим исследуем работу неподвижного вьюрка ложного кручения в неустановившемся режиме. Рассмотрим элементарную технологическую схему, приведенную на рис.1. При установившемся режиме работы для вращающегося вьюрка ( n=const, v=const ) крутка первого участка будет равна

K b = n

v а для неподвижного вьюрка будет определяться по формуле /3.33 /:

KH = ПХо

Т О Г Н ( 1 - e

1 - e^GJp

- - W )

где

Х 0 - естественное кручение оси нити в пункте входа на поверхность неподвижного вьюрка, об/м;

П - поправочный коэффициент;

T ) - осевая сила натяжения пряжи, Н;

• r _H - радиус нити, м;

• G - Модуль упругости пряжи при кручении, Н/м²;

• J - Полярный момент инерции площади поперечного сечения пряжи, м⁴ ;

• ^ - коэффициент трения между материалами вьюрка и пряжи;

• ^ - угол обхвата вьюрка нитью, рад.

  

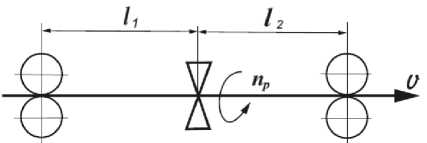
  Рис.1. Расчетная схема неподвижного вьюрка.

  Имея в виду, что при определенных условиях К н =const и приравняв правую часть (1) с левой частью (2) получаем:

  
  

n = K H v ,                     (3.)

то есть неподвижный вьюрок оказывает такое же действие, как и вращающийся вьюрок с частотой вращения, определяемой по (3).

Эту величину обозначим пР = KHv и назовем приведенной частотой вращения неподвижного вьюрка. Тогда при пуске для 1 участка пряжи можем составить уравнение

dk

n np - K 1 ^v 1 1

dt

где dK 1 - приращение крутки пряжи на первом участке за время dt ;

• 1 1 - длина этого участка;

v - скорость движения пряжи.

При начальных условиях: при t=0 K 1 =К_Н , уравнение имеет решение:

к = nnp v

1 —

1+KHv

Л - vt

e

l i

к

п

np у

При К_Н = 0 (5) принимает вид:

vt

K 1 = "■■■• ¹ v

- e

— li

к

Анализ (5) и (6) показывает,

у что крутка

первого

участка изменяется

экспоненциально и в установившемся режиме достигает значения nnр v

Изменение крутки K 1 показано на рис.2 линией I (для случая K H =0).

dk2 =

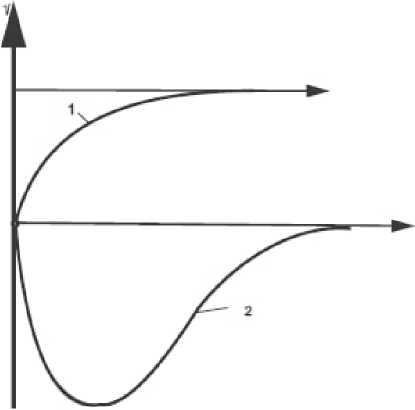
Рис.2. Зависимость крутки от времени при пуске Аналогично можем составить уравнение для второго участка:

K 1 v - n np

dt

v

Его решение при начальных условиях: при t=0 K 2 =К H имеет вид:

vt

K = K„e - l ² 2 H

ⁿ np     l 1

v ^l 1 - ¹ 2

1 +

к

K _H v

n

vt

vt

e

l ₁

-e

l ₂

np Д

7

При K H =0 (3.101) принимает вид:

K 2 =

ⁿпр     l 1

v ¹ 1 - ¹ 2

e

к

vt

l 1

- e

vt

l ₂

7

Их анализ показывает, что в отличие от установившегося режима работы ( t ^ А в пусковом режиме (при конечном t ) значение K 2 отлично от нуля. Кривая 2 на рис.2. показывает изменение крутки K 2 во времени (для случая K H = 0 ).

Приравняв нулю производную уравнения (9), то есть K1 = 0 , определим максимальное значение крутки K2m и момент времени, когда оно имеет место, tт=0 K2m

ⁿпр v

l 1

к

vt

l

—

— e

vtm

l ₁ l ₂          l ₂

t m    V 01 — 1 2 )    1 1

т. е., при неизменных l 1 и l 2 t m зависит только от скорости v , а абсолютная величина K 2m определяется соотношением l 1 и l 2. При l 1 = l 2= l :

^K 2 m

nпр

vt

v

te l

t

m

lv