Исследование динамики решетки оксифторида Rb 2KMoO 3F 3

Автор: Крылов Александр Сергеевич, Софронова Светлана Николаевна, Колесникова Евгения Михайловна, Исаенко Людмила Ивановна

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Технологические процессы и материалы

Статья в выпуске: 5 (45), 2012 года.

Бесплатный доступ

Получены полные спектры КР оксифторида Rb 2KMoO3F 3 в температурном диапазоне 7-260 K. При температуре T ~ 185 K был обнаружен структурный фазовый переход, рассчитана динамика решетки «разупорядо-ченного» кристалла Rb 2KMoO 3F 3, в спектре которого присутствуют «мягкие» моды колебаний.

Динамика решетки, оксифториды, комбинационное рассеяние света

Короткий адрес: https://sciup.org/148176953

IDR: 148176953

Текст научной статьи Исследование динамики решетки оксифторида Rb 2KMoO 3F 3

Эльпасолит Rb 2 KMoO 3 F 3 принадлежит к большому классу кристаллов эльпасолитов-криолитов с общей формулой A 2 BMO 3 F 3 (A, B = NH 4 , Na, K, Rb, Cs; M = Mo, W). В зависимости от отношения ионных радиусов R _A и R _B, а также от атома M, высокотемпературная кубическая фаза Fm 3 m данных соединений может оставаться стабильной вплоть до температуры жидкого гелия [1–6] или искажаться в результате одного [1–5; 7] или двух фазовых переходов [1–6; 8–10]. Например, несмотря на близкие значения ионных радиусов атомов ( R Mo = 0,073 nm) и W ( R W = 0,074 nm), эльпа-солит Rb₂KMoO₃F₃ испытывает фазовый переход [11], а эльпасолит Rb 2 KWO 3 F 3 не испытывает никаких фазовых превращений и остается кубическим вплоть до температуры жидкого гелия [12]. Необходимо отметить, что высокотемпературная кубическая фаза в данных соединениях реализуется благодаря разупорядочению атомов F/O по кристаллу. В зависимости от расположения атомов анионов F/O, локальная симметрия анионного октаэдра [MO 3 F 3 ]^3-может быть либо mer- (симметрия C ₂ _v ), либо fac-(симметрия C 3 v ) конфигурации. Авторами работы [13] было показано, что анионный октаэдр находится в fac- конфигурации.

Недавно выяснилось [11], что оксифторид Rb 2 KMoO 3 F 3 испытывает структурный фазовый переход типа порядок-беспорядок при T = 195 K, далекий от трикритической точки в режиме нагрева образца. Однако структуру низкотемпературной фазы решить не удалось ввиду двойникования образцов ниже температуры фазового перехода.

Целью настоящей работы является представление результатов экспериментальных и теоретических исследований динамики решетки эльпассолита Rb 2 KMoO 3 F 3 с помощью метода комбинационного рассеяния света и в рамках обобщенной модели Гордона–Кима для того, чтобы попытаться описать механизм фазового перехода в данном кристалле.

Исследование спектров КР оксифторида Rb 2 KMoO 3 F 3 . Спектры КР неориентированного кристалла оксифторида Rb 2 KMoO 3 F 3 были получены с помощью КР-спектрометра Horiba Jobin Yvon T64000.

В эксперименте был использован образец 1,5×1,5×1,5 мм № 7, описанный в работе [11]. В качестве источника возбуждения применялось излучение Ar+ лазера с длиной волны λ = 514,5 нм. Мощность на образце составляла 7 мВт.

Для того чтобы извлечь количественную информацию о спектральных параметрах из экспериментальных данных, спектры были разложены на отдельные линии. В диапазоне низких частот (< 150 см–1) в качестве модельной формы линии была использована модель затухающего гармонического осциллятора [14]. Выше 150 см–1 был использован контур Лоренца [15] (рис. 1).

Рис. 1. Спектр КР оксифторида Rb₂KMoO₃F₃ при комнатной температуре ( T = 300 K) и при T = 10 K:

а – диапазон решеточных колебаний; б – диапазон колебаний O–Mo–F; в – диапазон колебаний O–Mo–O; г – диапазон валентных колебаний Mo–F; e – диапазон валентных колебаний Mo–O [1])

Ранее [16] высокочастотная часть спектра, содержащая полносимметричные колебания связи Mo–O анионного октаэдра, была получена с низким разрешением (2 cm–1), и аппроксимирована только одним контуром Лоренца.

В данной работе эта часть спектра была прописана с лучшим разрешением (0,7 cm–1), и анализ данной области спектра показал, что в этом диапазоне, в кубической высокотемпературной фазе присутствует две линии (рис. 2), хотя это колебание в кубической фазе не вырождено.

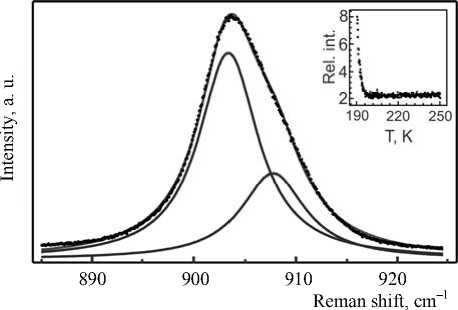
Рис. 2. Часть спектра, содержащая полносимметричное колебание Mo–O, разложенная на два контура Лоренца (на вставке – температурная зависимость относительной интенсивности данных линий)

При температуре T ≈ 185 K происходит фазовый переход кристалла Rb 2 KMoO 3 F 3 (рис. 3). Исходя из существенных изменений спектральных параметров, данный фазовый переход является переходом первого рода. Основные изменения происходят в области полносимметричных колебаний Mo–O и Mo–F, а также в области решеточных колебаний, где число линий удваивается, указывая на увеличение объема элементарной ячейки, как минимум, в два раза.

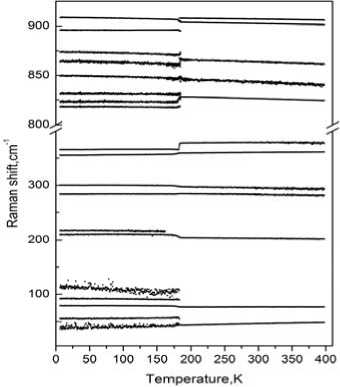
Рис. 3. Температурная трансформация спектра КР оксифторида Rb 2 KMoO 3 F 3

Хорошо виден резкий скачок в поведении частот в окрестности фазового перехода (рис. 4). Причем частота колебания Mo–O увеличивается ниже темпе- ратуры фазового перехода (рис. 4, а), а частота колебания Mo–F, наоборот, уменьшается (рис. 4, б). Данные зависимости были аппроксимированы с учетом трех- и четырех-фононного взаимодействий, которые возникают вследствие ангармонизма решетки в отсутствия фазовых превращений [17]. Согласно [18], сдвиг частоты Δω полносимметричного высокочастотного колебания (разница экспериментальных и теоретических значений) пропорциональна квадрату параметра порядка. Полученная зависимость (рис. 4, в) демонстрирует типичное поведение параметра порядка при фазовом переходе первого рода, далеком от трикритической точки.

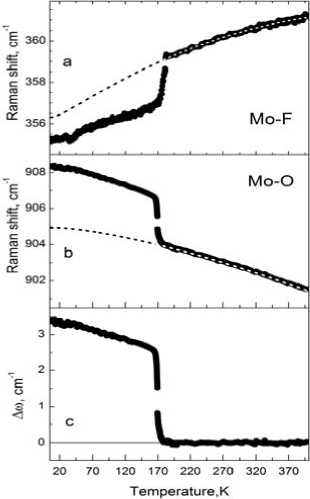
Рис. 4. Температурные зависимости частот полносимметричных колебаний Mo–F и Mo–O:

а , б – теоретические аппроксимации; в – разница между экспериментальной частотой колебания Mo–O и теоретической

Ширины полносимметричных колебаний Mo–O и Mo–F также испытывают аномалии в окрестности фазового перехода (рис. 5). Полученные температурные зависимости ширин линий не характерны для твердого тела. Наблюдается ярковыраженное аномальное λ-образное поведение ширины линии полносимметричного колебания Mo–O и, в меньшей степени, полносимметричного колебания Mo–F. Такие аномальные зависимости указывают на то, что обнаруженный фазовый переход является фазовым переходом типа порядок-беспорядок, и отражают критические флуктуации параметра порядка в окрестности точки фазового перехода [19].

В упорядоченных эльпасолитах при гелиевых температурах ширины полносимметричных колебаний анионного октаэдра стремятся к значениям ~1–3 см^–1[20–22]. Полносимметричное колебание 908 см^–1в данном случае является параметром, связанным со степенью упорядочения октаэдра [MoO 3 F 3 ]^3–.

Таблица 1

Атом	Координаты ( a ; b ; c )	«Мягкие» моды и соответствующие собственные векторы
Атом	Координаты ( a ; b ; c )	141 i (2)	141 i (2)	139 i (2)	98 i (2)	60 i (2)	59 i (2)	44 i (2)	33 i (2)
Rb	(0,25; 0,25; 0,.25)	⁽ x ;^- у ;⁰⁾	^(- ^x ;^- у ;⁰⁾	(0;0; z )	( x ;0;0)	(0;0; z )	( x ;0;0)	(- x ;0;0)	(0;0;0)
Rb	(0,25; 0,25; 0,75)	⁽ x ;^- у ;⁰⁾	^(- x ;^- у ;⁰⁾	(0;0;- z )	( x ;0;0)	(0;0;- z )	( x ;0;0)	( x ;0;0)	(0;0;0)
Rb	(0,25; 0,75; 0,25)	(- x ; у ;0)	⁽ x ; у ;⁰⁾	(0;0; z )	( x ;0;0)	(0;0;- z )	(- x ;0;0)	(- x ;0;0)	(0;0;0)
Rb	(0,25; 0,75; 0,75)	(- x ; у ;0)	⁽ x ; у ;⁰⁾	(0;0;- z )	( x ;0;0)	(0;0; z )	(- x ;0;0)	( x ;0;0)	(0;0;0)
Rb	(0,75; 0,25; 0,25)	(- x ; у ;0)	⁽ x ; у ;⁰⁾	(0;0;- z )	( x ;0;0)	(0;0; z )	(- x ;0;0)	( x ;0;0)	(0;0;0)
Rb	(0,75; 0,25; 0,75)	(- x ; у ;0)	⁽ x ; у ;⁰⁾	(0;0; z )	( x ;0;0)	(0;0;- z )	(- x ;0;0)	(- x ;0;0)	(0;0;0)
Rb	(0,75; 0,75; 0,25)	⁽ x ;^- у ;⁰⁾	^(- ^x ;^- у ;⁰⁾	(0;0;- z )	( x ;0;0)	(0;0;- z )	( x ;0;0)	( x ;0;0)	(0;0;0)
Rb	(0,75; 0,75; 0,75)	⁽ x ;^- у ;⁰⁾	^(- ^x ;^- у ;⁰⁾	(0;0; z )	( x ;0;0)	(0;0; z )	( x ;0;0)	(- x ;0;0)	(0;0;0)
К	(0,5 ;0,5; 0,5)	^(- x ; у ;^- z )	^(- x ;^- у ; z )	(0;0; z )	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0; z )	(- x ;0;0)
К	(0; 0; 0,5)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	(0;0;- z )	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0;- z )	( x ;0;0)
К	(0; 0,5; 0)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	(0;0; z )	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0; z )	( x ;0;0)
К	(0,5; 0; 0)	⁽ x ;^- у ;^- z )	⁽ x ; у ; z )	(0;0;- z )	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0;- z )	(- x ;0;0)
Mo	(0; 0; 0)	^(- ^x ; у ;^- z )	^(- ^x ;^- у ; z )	( x ;0;0)	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0;- z )	( x ;0;0)
Mo	(0,5; 0,5; 0)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	(- x ;0;0)	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0; z )	(- x ;0;0)
Mo	(0,5; 0; 0,5)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	( x ;0;0)	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0;- z )	(- x ;0;0)
Mo	(0; 0,5; 0,5)	⁽ ^x ;^- у ;^- z )	⁽ x ; у ; z )	(- x ;0;0)	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0; z )	( x ;0;0)
O/F	(0,208; 0; 0)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	(- x ;0;0)	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0;- z )	(- x ;0;0)
O/F	(0; 0,208; 0)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	(- x ;0;0)	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0;- z )	( x ;0;0)
O/F	(0; 0; 0,208)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	(- x ;0;0)	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0; z )	( x ;0;0)
O/F	(0,708; 0,5; 0)	⁽ ^x ;^- у ;^- z )	⁽ x ;у ; z )	( x ;0;0)	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0; z )	( x ;0;0)
O/F	(0,5; 0,708; 0)	⁽ ^x ;^- у ;^- z )	⁽ x ;у ; z )	( x ;0;0)	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0; z )	(- x ;0;0)
O/F	(0,5; 0,5 ;0,208)	⁽ x ;^- у ;^- z )	⁽ x ;у ; z )	( x ;0;0)	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0;- z )	(- x ;0;0)
O/F	(0,708; 0; 0,5)	^(- x ;у ;^- z )	^(- ^x ;^- у ; z )	(- x ;0;0)	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0;- z )	( x ;0;0)
O/F	(0,5; 0,208; 0,5)	^(- x ;у ;^- z )	^(- ^x ;^- у ; z )	(- x ;0;0)	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0;- z )	(- x ;0;0)
O/F	(0,5; 0; 0,708)	^(- x ;у ;^- z )	^(- x ;^- у ; z )	(- x ;0;0)	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0; z )	(- x ;0;0)
O/F	(0,208; 0,5; 0,5)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	( x ;0;0)	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0; z )	(- x ;0;0)
O/F	(0; 0,708; 0,5)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	( x ;0;0)	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0; z )	( x ;0;0)
O/F	(0; 0,5; 0,708)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	( x ;0;0)	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0;- z )	( x ;0;0)
O/F	(0,792; 0; 0)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	(- x ;0;0)	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0;- z )	(- x ;0;0)
O/F	(0; 0,792; 0)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	(- x ;0;0)	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0;- z )	( x ;0;0)
O/F	(0; 0; 0,792)	⁽ x ;^- у ; z )	⁽ x ; у ;^- z )	(- x ;0;0)	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0;- z )	( x ;0;0)
O/F	(0,292; 0,5; 0)	⁽ ^x ;^- у ;^- z )	⁽ x ;у ; z )	( x ;0;0)	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0; z )	( x ;0;0)
O/F	(0,5; 0,292; 0)	⁽ ^x ;^- у ;^- г )	⁽ x ;у ; z )	( x ;0;0)	( x ;0;0)	(0; у ;0)	(0; у ;0)	(0;0; z )	(- x ;0;0)
O/F	(0,5; 0,5; 0,792)	⁽ x ;^- у ;^- z )	⁽ x ;у ; z )	( x ;0;0)	( x ;0;0)	(0;- у ;0)	(0; у ;0)	(0;0; z )	(- x ;0;0)
O/F	(0,292; 0; 0,5)	^(- x ;у ;^- z )	^(- ^x ;^- у ; z )	(- x ;0;0)	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0;- z )	( x ;0;0)
O/F	(0,5; 0,792; 0,5)	^(- x ;у ;^- z )	^(- ^x ;^- у ; z )	(- x ;0;0)	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0;- z )	(- x ;0;0)
O/F	(0,5; 0; 0,292)	^(- x ;у ;^- z )	^(- x ;^- у ; z )	(- x ;0;0)	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0;- z )	(- x ;0;0)
O/F	(0,792; 0,5; 0,5)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	( x ;0;0)	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0; z )	(- x ;0;0)
O/F	(0; 0,292; 0,5)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	( x ;0;0)	( x ;0;0)	(0;- у ;0)	(0;- у ;0)	(0;0; z )	( x ;0;0)
O/F	(0; 0,5; 0,292)	^(- x ; у ; z )	^(- x ;^- у ;^- z )	( x ;0;0)	( x ;0;0)	(0; у ;0)	(0;- у ;0)	(0;0; z )	( x ;0;0)

Собственные вектора «мягких» мод колебаний ( Z = 4)

Ширина линии данного колебания ~ 6 см-1 при гелиевых температурах. Так как это значение в несколько раз превышает значения ширин линий полностью упорядоченных эльпасолитов, можо предположить, что полного упорядочения анионных октаэдров в исследуемом соединении не происходит даже при гелиевых температурах.

Расчет динамики решетки в рамках обобщенной модели Гордона-Кима. Для расчета динамики решетки эльпасолита Rb 2 KMoO₃F₃ был использован обобщенный метод Гордона-Кима [23].

В высокотемпературной кубической фазе атомы F/O разупорядочены по всему кристаллу. Вследствие этого беспорядка, каждый октаэдр может равновероятно находиться в 20 различных состояниях (8 состояний с тригональной симметрией и 12 состояний с орторомбической симметрией C ₂ v ).

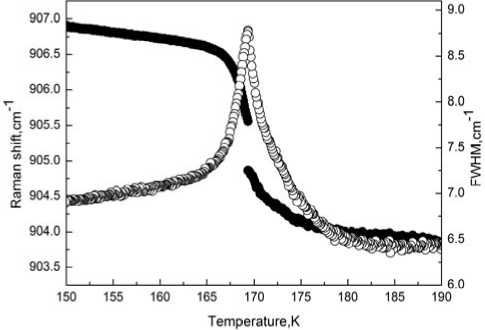
Рис. 5. Температурные зависимости частоты и ширины полносимметричного колебания Mo-O (белые кружки -ширина; черные кружки - частота)

В работе [13] было показано, что октаэдр [MoO 3 F 3 ]^3– преимущественно обладает тригональной симметрией (fac-конфигура-ция), поэтому в дальнейшем мы будем рассматривать только fac-конфигурации октаэдра.

Как уже было сказано, атомы анионов F/O разупо-рядочены по кристаллу в высокотемпературной кубической фазе. Для моделирования аналогичной ситуации в теории, была выбрана кубическая элементарная ячейка типа эльпасолита-криолита, содержащая четыре формульные единицы (Z = 4).

Чтобы смоделировать «усреднение» в кубической фазе Fm 3 m , мы вычисляли динамические матрицы (собственные значения которых и являются частотами колебаний) 4096 структур, в которых перебирались все возможные ориентации октаэдра в fac- состоянии (4 октаэдра в элементарной ячейке, и каждый может находиться в 8 равновероятных ориентациях). Затем мы усредняли динамические матрицы и определяли частоты колебания.

Параметр решетки сохранялся кубическим, и определялся из условия минимума полной энергии ( a cub = 8,427 Å). Расчетный спектр «мягких» мод содержит частоты, принадлежащие как центру зоны Бриллуэна, так и ее граничным точкам. Поэтому в исследуемом кристалле возможны фазовые переходы с увеличением объема элементарной ячейки. Смещения атомов, соответствующие собственным векторам «мягких» мод представлены в табл. 1.

Таким образом, в кристалле эльпасолита Rb 2 KMoO 3 F 3 был обнаружен фазовый переход типа порядок-беспорядок при температуре T ≈ 185 K в режиме охлаждения образца. Исходя их теоретических и экспериментальных результатов, можно предположить, что данный фазовый переход связан с изменениями в молекулярном октаэдре [MoO 3 F 3 ]^3–и может сопровождаться увеличением объема элементарной ячейки. В настоящее время вопрос об упорядочении F/O октаэдров и их роли при структурном фазовом переходе остается открытым. Необходимы дальнейшие исследования для определения симметрии низкотемпературной фазы и для понимания природы обнаруженного фазового превращения.

Статья научная