Исследование динамики системы управления объектом второго порядка с учетом расположения действительных полюсов

По многочисленным источникам научной и технической литературы можно выделить следующие методы синтеза ПИД-регуляторов [1-10]: эмпирическая настройка; методы Зиглера-Никольса [1] и производные методы [2]; алгебраические методы; методы модального синтеза; методы синтеза в частотной области; методы оптимального синтеза; метод оптимальной ПФ замкнутой системы (технический и симметричный оптимумы). Основные тенденции развития методов синтеза ПИ- и ПИД-регуляторов - в книге Aidan O’Dwyer, 2006 [7] (443 метода синтеза ПИД-регуляторов) и в издании Aidan O’Dwyer, 2009 [8] (1731 метод синтеза ПИД-регуляторов).

Одним из методов синтеза ПИД-регуляторов, активно развиваемым учеными, является модальный метод [3, 9]. В научных работах, посвященных синтезу регуляторов, отсутствуют соотношения, связывающие значения переходной характеристики и коэффициентов объекта управления с учетом расположения действительных полюсов.

При теоретическом описании мобильных, строительных и дорожных, дорожностроительных машин как объектов управления наиболее распространенными являются математические модели второго и более высокого порядка [9-13].

Рассматривается линейная система автоматического управления с передаточной функцией (ПФ) объекта второго порядка.

Передаточные функции объекта управления второго порядка W o ( 5 ) и ПИД-регулятора W_y ( 5 ) таковы:

W o ( ^ ) =

ь05 + bl     .

• 2 .              .          ;

а о 5 + a i 5 + a 2

^Kd s + K p s + K '

Wy (5) = Kp + K + KdS = s где 5 - оператор Лапласа; Kp, Ki и Kd - коэффициенты соответственно пропорциональности, интегрирования и дифференцирования.

При последовательном соединении ПФ объекта и ПИД-регулятора образуют разомкнутую систему с ПФ следующего вида:

W ( 5 ) = W o ( 5 ) W y ( 5 ) =

K d b 0 5 ³ + (K b + K p b ₀) 5 ² + ( Kb 0 + K p b , ) 5 + Kb

3         2

a ₀ 5 + a , 5 + a ₂ 5

Передаточная функция замкнутой системы управления с единичной обратной связью к (s) =

W ( s ) 1 + W ( s )

K d b 0 s ³ + ( K d b , + K p b ₀) s ² + ( Kb 0 + K p b ) s + Kb

⁽ a 0 ⁺ K d b 0 ) ^{s 3 + (} a l ^{+ K}d^b 1 ⁺ K p b 0 ) ^{s 2 + (} a 2 ⁺ K i b 0 ^{+ K}p^b1 ) ^{s + K}i^b1 "

Исходными данными для синтеза ПИД-регулятора САУ являются ПФ объекта управления W o ( 5 ) второго порядка и заданные показатели качества: перерегулирование и время регулирования.

Решается задача определения значений коэффициентов ПИД-регулятора Kd, Kp, Ki, обеспе- p чивающих заданные показатели качества по заданным ПФ объекта управления второго порядка Wo(5) и значениям действительных полюсов 51 =—п1, 52 =—П2, 53 =—П3 ПФ замкнутой системы управления.

Вывод основных соотношений методики параметрического синтеза регулятора и определение составляющих переходной характеристики h ( t ) замкнутой системы управления с ПИД-регулятором при задании действительных полюсов подробно описаны в работе [14].

Значения всех заданных трех полюсов являются действительными:

⁵ i =— n i ; ⁵ 2 =^- П 2 ; ⁵ з = ^- П з ^-

В работе [14] в результате аналитических преобразований получены следующие равенства:

а , + K d bx + K p b0 -------------p— = П1 + n2 + Пз ; а о + K d b o         1    2    3 а 2 + K i b0 + Kb , p = П з Сп , + П 2)+ П 1 П 2 ;                                              (1) a 0 + K d b, Kb . . K b = П1П2П3 -

Представим равенства (1) в виде системы уравнений, в которой неизвестны значения коэффициентов ПИД-регулятора:

K d [ b - b о (П 1 + П 2 + П з )] + K p b 0 = а о (п + п₂ + П з ) - а ;

• ^- K d b о ( П з ⁽П 1 + п₂⁾⁺П1П₂ ) + K p b i + K i b о = a о ⁽П з ⁽П 1 + n₂⁾+nin₂⁾ - a ₂;           <²>

• -    Kb    + Kb = a

d ^{о П 1 П} 2 ^п 3+ i ¹ -a ^{о П 1 П} 2 ^п 3 .

Введем обозначения с целью представления системы уравнений (2) в матричной форме:

Л = Ь - ь о (П 1 + п₂ + П з ); Л 2 = ь о ; Л з = 0; с = a o (n + п + П з ) - а ;

Л 1 = ^{- Ь} 0 ( П з ⁽П 1 ⁺ П 2 ⁾⁺П1П 2 ) ; ^Л 22 = ^Ь 1 ; ^Л 2з = ^Ь о ; с 2 = а 0 ⁽П з ⁽П 1 ⁺ П 2 ⁾⁺П1П 2 ) — a 2 ;    ⁽³⁾

Л ; 1 = ^- Ь о^П^2 ^П з ; Л |2 = ⁰; Л )з = ^Ь 1 ; с з = a 0 ^П1^П 2 ^П з "

С учетом обозначений (3) сформируем матрицы к  ^12

Л d = ^21  z

к Л 1   ^ 32

4'

л

< J

; C d =

(c с2 ; К, - к C 3 J

f K )

K p

к > J

где Λ _d и C_d – матрица и вектор-столбец известных параметров объекта управления и заданных значений действительных полюсов соответственно; K ₁ - вектор-столбец искомых значений коэффициентов ПИД-регулятора.

Матричное уравнение для определения искомых значений коэффициентов регулятора:

(Л d • K1) = Cd, а его решение представляется в следующем виде:

K 1 = Л d ^-1 C d .

Система уравнений (1) значительно упрощается при b ₀ = 0:

a + Kb

• - —— = П 1 + П 2 + П з ;

a a 2 + K Ь1

---------=П з (П 1 + П 2Н1 П 2 ;

a

Kb

— = П1П2П3- a 0

В этом случае формулы для определения значений коэффициентов ПИД-регулятора имеют следующий вид:

Kd _ c ¹ d b i

а о ⁽П ⁺ П 2 ⁺ П з ) ^- a i .

bi                ’ a [lUk ■ ik)-1! П2] a-.

“ p    b i                   b i               ’

c ₂

K _ c ₃ _ a ₀П 1 П₂П₃

i b 1            b 1       '

Получены выражения для расчета коэффициентов ПИД-регулятора, включающие коэффициенты ПФ объекта второго порядка при заданных значениях действительных полюсов. Выполнена проверка рассмотренной методики на конкретном примере.

Пример. Задан объект управления второго порядка с ПФ:

b₀ s + Ь 1    _     0,01 s + 0,7

a 0 s ² + a i s + a 2    0,04 s ² + 0,12 s + ¹

Требуется синтезировать ПИД-регулятор, который обеспечит переходную характеристику без перерегулирования, а время регулирования t p = 1 c.

Для реализации метода синтеза применены зависимости, опубликованные в работе [14], и зависимости (4). Расчеты выполнены в среде программы MathCAD.

Исходные данные для действительных значений полюсов:

значение n i определено с учетом желаемого времени регулирования, равного 1 с, и расчета по известной приближенной формуле [15-17]

t «      ,П = Re(»), р Re(s) 1

где Re( 5 ) - действительная часть полюса, наиболее приближенного к мнимой оси корневой плоскости; значения n₂ и П 3 определяются из требуемого значения перерегулирования и влияния этих полюсов на полюс n i

П 1 = 3; П 2 = 4; П₃ = 5; b = 0,7; b О = 0,01; a ₀ = 0,04; а 1 = 0,12; a 2 = 1,0.

Для заданных действительных полюсов определены коэффициенты ПИД-регулятора

К 1 =

(к а

K p

К

V K i J

5,783

32,517

; К, = 5,783; К = 32,517; К, = 53,0. dpi

Установившееся значение h_5tab = 1.

stab

Выполнено моделирование переходного процесса для периода времени t = 0, 0.001..3.

Переходная характеристика h(t ) при заданных действительных полюсах, составляющих h _n ( t ), h _l2 (t ), h _1з (t ), обусловленных действительными полюсами 5 1 = - n 1 , 5 ₂ = — П ₂, 5 3 = - П 3 , определяется по зависимостям, полученным в работе [14].

При t = ⁰ получим h ( t ) = h stab. + h П 1 ( t ) + h П 2 ( t ) + h П 3 ( t ) = 1 - 0,809 + 1,876 - 1,132 = 0,935.

Начальное значение h init [14] переходной характеристики h ( t )

^hinit .

K d b 0

a 0 + K d b 0

= 0,935.

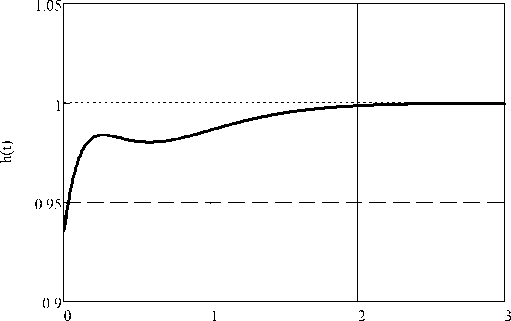
На рис. 1 представлен график переходной характеристики h(t ) замкнутой САУ с синтезированными параметрами ПИД-регулятора.

В рассмотренном примере начальное значение h init переходной характеристики h(t ) замкнутой САУ (рис. 1) входит в 5%-ю зону с оценкой времени регулирования, равного 0,04 с. В примере требования по качеству динамических характеристик могут быть повышены.

При известном значении b ₀, заданных параметрах объекта второго порядка и действительных полюсов в рассмотренном в примере время переходного процесса, исходя из условия 5%-й зоны установившегося значения, равно 0,04 с при желаемом 1 с.

Исследование влияния расположения действительных полюсов при реализации методики параметрического синтеза ПИД-регулятора [14] является актуальной задачей.

Для исследования влияния на динамику процесса управления объектом второго порядка действительных полюсов выполнено моделирование в среде MathCAD.

Задана ПФ объекта управления второго порядка

t, s

Рис. 1. График переходной характеристики синтезированной системы с заданными действительными полюсами

• Fig. 1.    Graf of step response of the synthesized system with given real poles

  W o ( 5 ) =

  
  

  b 0 5 + b 1

  a о 5 + a i 5 + a 2

  
  

0,01 ^{5 +} 0,7    .

0,04 5 ² + 0,12 5 + 1

Требуется исследовать систему управления с синтезированным ПИД-регулятором объектом второго порядка. Заданы варьируемые значения времени регулирования t _P, действительных полюсов η 1 , η 2 , η 3 .

Исходные соотношения компьютерного моделирования с учетом практики модального управления в среде MathCAD.

33η   η и ~-----, П1 = Re(s), tp ~ —; tp var 0,5...1.5; — =1...5, сшагом 1; — =1...5, с шагом 1.

Р    1    РР

Re( s )                    η₁                     η₁η₁

В соответствии с заданными соотношениями варьируемых переменных сформированы исходные данные девяти опытов (табл. 1).

Для реализации метода синтеза применены зависимости (5). Расчеты выполнены в среде программы MathCAD. Получены графики переходной характеристики: h ₁(t) при t _P=0,5 с; h ₂(t) при t P =1,0 с; h 3 (t) при t P =1,5 с.

Результаты моделирования переходной характеристики представлены: опыты 1, 2 – рис. 2; опыты 3, 4 – рис. 3; опыты 5, 6 – рис. 4; опыты 7, 8 – рис. 5; опыт 9 – рис. 6.

Обозначение на графиках: h1.01(t) – переходная характеристика при t _P=0,5 с, опыт 1; h2.01(t) – при t P =1,0 с, опыт 1; h3.01(t) – при t P =1,5 с, опыт 1. Аналогично во всех графиках в индексе меняется номер опыта.

Моделирование переходной характеристики замкнутой САУ с синтезированным по рассмотренной методике ПИД-регулятором, в заданном диапазоне времени регулирования от 0,5 до 1,5 с, соотношений действительных полюсов η 2 / η 1 = 1...5, η 3 / η 1 = 1...5 показало следующие результаты:

• -    динамический процесс имеет апериодический характер;

Таблица 1. Исходные данные для исследования

Table 1. Background data for the study

Номер опыта	Показатели
	Время регулирования t Р, с	Полюс η 1 , с-1	Полюс η 2 , с-1	Полюс η 3 , с-1
1	2	3	4	5
1	0,5	6	6	6
	1,0	3	3	3
	1,5	2	2	2
2	0,5	6	6	12
	1,0	3	3	6
	1,5	2	2	4
3	0,5	6	12	12
	1,0	3	6	6
	1,5	2	4	4
4	0,5	6	12	18
	1,0	3	6	9
	1,5	2	4	6
5	0,5	6	18	18
	1,0	3	9	9
	1,5	2	6	6
6	0,5	6	18	24
	1,0	3	9	12
	1,5	2	6	8
7	0,5	6	24	24
	1,0	3	12	12
	1,5	2	8	8
8	0,5	6	24	30
	1,0	3	12	15
	1,5	2	8	10
9	0,5	6	30	30
	1,0	3	15	15
	1,5	2	10	10

• -    перерегулирование практически отсутствует или имеет очень небольшое значение;

• -    увеличение значений действительных полюсов от η₂ = η₃ = η₁ до η₂ = 3·η₁ и η₃ = 4·η₁ приводит к постепенному уменьшению времени регулирования и улучшению динамики переходного процесса;

• -    для варианта задания времени регулирования 0,5 с и 1 с переходная характеристика h ( t ) в опытах 4, 5, 6 имеет удовлетворительное соответствие желаемому значению;

• -    хорошее соответствие заданию получено в опыте 6 при η 2 = 3·η 1 , η 3 = 4·η 1 ;

  0.5

  
  
  
0.95 0.5

^^^^^™ h1.01(t) h2.01(t) h3.01(t) h1.02(t)

■^^^^^^^^^^^^ h2.02(t) h3.02(t)

1.05

t, s

Рис. 2. График переходной характеристики (опыт 1 и 2)

• Fig. 2.    Graf of step response (experiment 1 and 2)

  

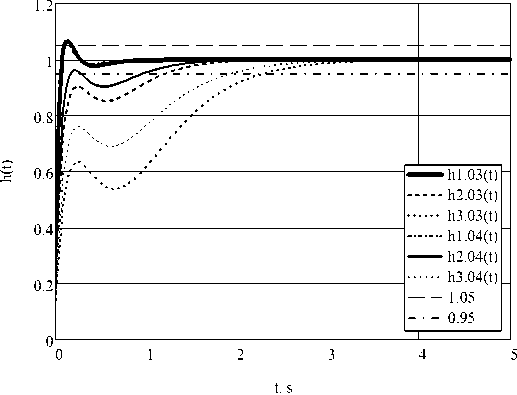
  Рис. 3. График переходной характеристики (опыт 3 и 4)

  
  

• Fig. 3.    Graf of step response (experiment 3 and 4)

  
  

  0.8

  0.6

  0.4

  0.2

  		—
  			■^^^^^^^ h1.05(t) h2.05(t) h3.05(t) h1.06(t) h2.06(t) h3.06(t) 1.05 0.95

  
  
  
  

  t, s

  Рис. 4. График переходной характеристики (опыт 5 и 6)

  
  

  Fig. 4. Graf of step response (experiment 5 and 6)

  1.2

  

  0.8

  0.6

  0.4

  
  

  0.2

  
  
  
  
  
  
  
  

  h1.07(t) h2.07(t) h3.07(t) h1.08(t) h2.08(t) h3.08(t) 1.05

  0.95

  
  
  
  
  
  
  
  

  t, s

  
  

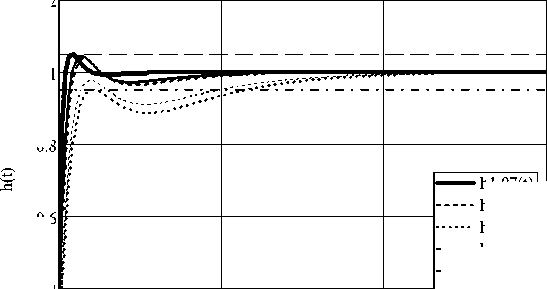
  Рис. 5. График переходной характеристики (опыт 7 и 8)

  Fig. 5. Graf of step response (experiment 7 and 8)

  
  

t, s

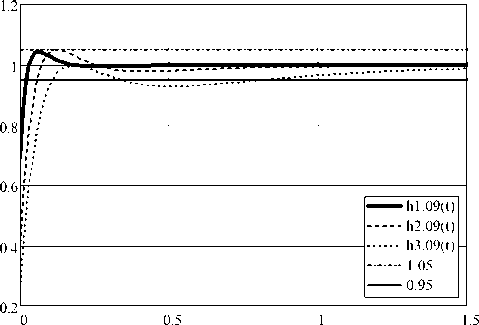
Рис. 6. График переходной характеристики (опыт 9)

Fig. 6. Graf of step response (experiment 9)

• -    в опытах 7, 8, 9 наблюдается постепенное уменьшение времени регулирования и улучшение переходного процесса без перерегулирования;

• -    при всех значениях варьируемого значения полюса п 1 переходная характеристика находится в 5%-й зоне.

Рассмотрена методика модального синтеза параметров ПИД-регулятора по заданным значениям параметров объекта второго порядка и действительных полюсов замкнутой системы управления. Методика реализована в программной среде MathCAD.

Исследование динамики переходного процесса САУ объектом второго порядка с параметрами ПИД-регулятора, полученными по предлагаемой методике синтеза, показало работоспособность в рассмотренном диапазоне динамических характеристик.

Для дальнейших научных исследований особенностей методики параметрического синтеза ПИД-регулятора и реализации положений методики для инженерного применения с учетом современных вычислительных возможностей компьютерной техники планируется разработка методики модального синтеза с размещением комплексных полюсов, выполнение задачи оптимизации назначения полюсов при исходном задании первого полюса по известным зависимостям по времени регулирования с проверкой на положительные значения коэффициентов ПИД-регулятора, устойчивости системы управления по алгебраическому критерию Рауса.

• [1]    Ziegler J. G., Nichols N. B. Optimum settings for automatic controllers, Transactions of the American society of mechanical engineers , 1942, 64, 759–768.

• [2]    Astrom K. J., Hagglund T. Advanced PID Control. Research Triangle Park, North Carolina: The Instrumentation, Systems, and Automation Society, 2006. 354 p.

• [3]    Вадутов О. С. Синтез ПИД-регулятора в системах с запаздыванием методом условной оптимизации с ограничениями на размещение полюсов. Известия Томского политехнического университета. Информационные технологии , 2014, 325(5), 16–22. [Vadutov O. S. Design of PID controller for delayed systems using optimization technique under pole assignment constraints. Izvestiya Tomskogo politekhnicheskogo universiteta. Informatsionnye tekhnologii , 2014, 325(5), 16–22 (in Russian)].

• [4]    Филипс Ч., Харбор Р. Системы управления с обратной связью . М.: Лаборатория базовых знаний, 2001. 616 с. [Filips Ch., Kharbor R. Feedback control systems . Moscow, Laboratoriya bazovykh znaniy Publ., 2001, 616 p. (in Russian)].

• [5]    Воронов А. А. Основы теории автоматического управления. Автоматическое регулирование непрерывных линейных систем . М.: Энергия, 1980. 309 с. [Voronov A. A. Fundamentals of the theory of automatic control. Automatic control of continuous linear systems . Moscow, Energiya Publ., 1980, 309 p. (in Russian)].

• [6]    Лукас В. А. Теория автоматического управления . М.: Недра, 1990. 416 с. [Lukas V. A. Automatic control theory . Moscow, Nedra Publ., 1990, 416 p. (in Russian)].

• [7]    O’Dwyer A. Handbook of PI and PID ControllerTuning Rules . London: Imperial College Press, 2006. 564 p.

• [8]    O’Dwyer A. Handbook of PI and PID controller tuning rules . London: Imperial College Press, 2009. 623 p.

• [9]    Прокопьев А. П., Иванчура В. И., Емельянов Р. Т. Синтез ПИД-регулятора для объектов второго порядка с учетом расположения полюсов, Журнал СФУ. Техника и технологии, 2016, 9(1), 50–60. DOI: 10.17516/1999-494X-2016-9-1-50-60. [Prokopiev A. P., Ivanchura V. I., Emelyanov R. T. Synthesis PID controller for objects second order with regard to the location poles. Zhurnal SFU. Tekhnika i tekhnologii , 2016, 9(1), 50–60. DOI: 10.17516/1999-494X-2016-9-1-50-60 (in Russian)].

• [10]    Замятин Д. В., Ловчиков А. Н. Методика синтеза оптимальных по быстродействию систем, Вестник СибГАУ , 2005, 4, 28–30. [Zamyatin D. V., Lovchikov A. N. The time optimal systems synthesis methodic. Vestnik SibGAU , 2005, 4, 28–30 (in Russian)].

• [11]    Замятин Д. В., Ловчиков А. Н. Определение параметров корректирующего устройства для системы четвертого порядка, оптимальной по быстродействию, Вестник СибГАУ , 2006, 4(11), 18–20. [Zamyatin D. V., Lovchikov A. N. Correctional unit parameters obtaining for time optimal four order system. Vestnik SibGAU , 2006, 4(11), 18–20 (in Russian)].

• [12]    Замятин Д. В., Ловчиков А. Н. Синтез оптимальных по быстродействию систем высокого порядка, Вестник СибГАУ , 2013, 2(48), 24–28. [Zamyatin D. V., Lovchikov A. N. Synthesis of time optimal systems of high order. Vestnik SibGAU , 2013, 2(48), 24–28 (in Russian)].

• [13]    Иванчура В. И., Прокопьев А. П. Оптимизация следящей системы автоматического управления, Вестник СибГАУ , 2011, 5 (38), 44–49. [Ivanchura V. I., Prokopiev A. P. Optimization of a tracker system of automatic control. Vestnik SibGAU , 2011, 5(38), 44–49 (in Russian)].

• [14]    Прокопьев А. П., Иванчура В. И., Емельянов Р. Т., Скурихин Л. В. Методика синтеза регуляторов для объектов второго порядка, Вестник СибГАУ , 2016, 17(3), 618-624. [Prokopiev A. P., Ivanchura V. I., Emelianov R. T., Scurihin L. V. The technique of synthesis of regulators for objects of the second order. Vestnik SibGAU , 2016, 17(3), 618–624 (in Russian)].

• [15]    Ефимов С. В., Замятин С. В., Гайворонский С. А. Синтез ПИД-регулятора с учетом расположения нулей и полюсов системы автоматического регулирования, Известия Томского политехнического университета, 2010, 317 (5), 102-107. [Efimov S. V., Zamyatin S. V., Gayvoronskiy S. A. Synthesis of the PID controller with respect to the location of zeros and poles of the system of automatic control. Izvestiya Tomskogo politekhnicheskogo universiteta , 2010, 317(5), 102–107 (in Russian)].

• [16]    Ефимов С. В., Гайворонский С. А., Замятин С. В. Задачи корневого анализа и синтеза систем автоматического управления, Известия Томского политехнического университета , 2010, 316(5), 16–20. [Efimov S. V., Gayvoronskiy S. A., Zamyatin S. V. Root tasks of analysis and synthesis and synthesis of automatic control systems. Izvestiya Tomskogo politekhnicheskogo universiteta , 2010, 316(5), 16–20 (in Russian)].

• [17]    Удерман Э. Г. Метод корневого годографа в теории автоматических систем . М.-Л.: Госэнергоиздат, 1963. 112 с. [Uderman E. G . Root locus method in the theory of automatic systems. Moscow-Leningrad, Gosenergoizdat Publ., 1963, 112 p. (in Russian)].