Исследование динамики управляемого углового движения космического аппарата с вращающимся солнечным парусом

Ранее в работах [1, 2] было найдено точное аналитическое решение уравнения в частных производных для поперечных колебаний вращающейся мембраны с центральной жесткой вставкой. В радиальном направлении решение было получено в виде ряда, по локальным функциям Хейна. (К. Heun). В тангенциальном направлении решение сводится к волновому уравнению с периодическими граничными условиями. На основе полученного аналитического решения разработана математическая модель в виде набора независимых гироскопически связанных мод движения или, другими словами, разработан механический аналог вращающегося пленочного диска, в виде набора, гироскопов в упругих подвесах, каждый со своим приведенным моментом инерции и жесткостью подвеса. Из нормировки полученных мод движения на. приведенные массы (моменты инерции) строго следует, что 99,9% массы пленочного диска, паруса, совершает колебания на. первых двух гироскопически связанных кососимметрических формах колебаний паруса (с одним узловым диаметром и без узловых окружностей). Это позволило с большой степенью точности заменить описание динамического поведения объекта, управления как системы с распределенными параметрами его описанием как КА с одним гироскопом в упругом подвесе (вращающийся мембранный диск солнечного паруса) и управляющим силовым гироскопом в подвесе Гука, с равным по величине и противоположно направленным кинетическим моментом.

Базовая конструкция космической платформы как объекта, управления, показанная на. рис. 1, включает в себя собственно солнечный парус, который представляет собой вращающийся пленочный диск с центральной жесткой вставкой, приборный отсек с целевой аппаратурой и компенсирующим гироскопом во внутреннем кардановом подвесе (сочленение Гука) с регулируемой скоростью вращения ротора. Солнечный парус и компенсирующий силовой гироскоп вращаются в противоположных направлениях, образуя «спарку» [3, 4].

Такая конструкция обладает скрытым кинетическим моментом. Внутренний карданов подвес с управляемыми и контролируемыми углами поворота, предназначен для отклонения оси вращения ротора силового гироскопа от оси вращения центральной жесткой вставки паруса, с целью создания управляющего гироскопического момента. Центральная вставка, паруса, выполненная в виде вантовой конструкции, служит для передачи момента, импульса. приборному отсеку. Рабочая поверхность солнечного паруса, представляет собой в развернутом состоянии сплошной круглый пленочный диск радиусом R = 50 м, радиус центральной жесткой вставки а = 5 м, толщи на пленки Һ = 1.2 • 10^-5 м и плотность материала р = 1.4 • 103 кг/м³. Диск вращается с угловой скоростью П = 0.5 рад/с, вследствие чего материал паруса, (полиамидная пленка) находится в напряженно-деформированном состоянии.

Рис. 1. Базовая конструкция космической платформы с вращающимся солнечным парусом

3.    Уравнения движения КА с солнечным парусом вокруг центра масс

Введем систему координат OXYZ, связанную с осями чувствительности датчиковой аппаратуры, следующим образом. Ось OX направим в сторону, противоположную оси вращения центральной вставки паруса, ось OY в плоскости ее вращения, а ось OZ дополняет систему осей до правой тройки. Оси этой системы координат для вращающейся мембраны являются осями Резаля.

Рассмотрим угловое движение КА вокруг поперечных осей аппарата, полагая, что вокруг продольной оси система, управления с достаточной степенью точности удерживает аппарат. «Разобьем» объект управления на два тела и рассмотрим каждое по отдельности: тело 1 — солнечный парус, тело 2 — приборный отсек вместе с силовым гироскопом. На рис. 2 представлена динамическая схема объекта управления, где ш — угловая скорость вращения аппарата. Q — относительная угловая (скорость вращения паруса.. ш_рот — относительная угловая скорость вращения ротора силового гироскопа, р — угол отклонения плоскости вращения мембранного диска, 3 — угол отклонения ротора силового гироскопа в подвесе Гука.

В Приложении на. основе материалов работы [1] приводится строгий вывод описания системы с распределенными параметрами, а именно вращающегося мембранного диска с жесткой центральной вставкой в виде набора, гироскопов в упругих подвесах, каждый со своим приведенным моментом инерции и жесткостью подвеса. При этом доказывается, что 99,9% массы мембраны совершают колебания на. первых двух гироскопически связанных кососимметричных модах движения, что позволяет с высокой степенью точности описать динамическое поведение мембранного диска, динамикой одного гироскопа, в упругом подвесе.

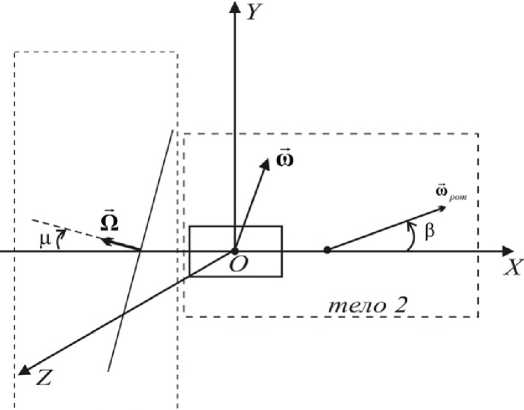
тело 1

Рис. 2. Динамическая схема объекта управления в системе координат OXYZ

На основании этого вывода кинетический момент тела. 1 можно представить в виде

Һ1 = MJ1(Q + Мтш), где M — матрица малого поворота вектора, Ji   приведенный момент инерции паруса, ш — угловая скорость вращения аппарата.

1   -фг   фу фх - П + ф"х " А 0   0" м = фг    1   - фх , ш = фу , П = фу ,  J1 = 0С 0 _-фу   ф,     1 . Фг_ фг 0  0 С где А л С — осевой и экваториальный моменты инерции паруса (А = 2С).

После линеаризации, полагая фх = 0, с точностью до второго порядка малости получаем кинетический момент паруса:

• —АП + Аф" _х + Аф_х

  
  

  ^ 1 =

  
  

• —А П фг + Сфу + Сфу АПфу + Сфг + Сфг

Кинетический момент тела. 2 вычисляется по следующей формуле:

h2 = .Кш + BH, где J2 момент инерции КА, B — матрица направляющих косинусов малых угловых отклонений ротора силового гироскопа в подвесе Гука, H — кинетический момент ротора

силового гироскопа в подвесе	Гука в связанной с	НИМ	системе координат,
"Ах   0	0 1            Г 1	-Зг	Зу 1           "н 1
J 2 =  0  Ау	0  , B =   Зг	1	—Зх , н =  0
00	Аг_         -Зу	Зг	10

После линеаризации с точностью до второго порядка малости, а также учитывая, что З_х = 0, получаем кинетический момент тела 2:

Ах

0

0

Фх

1

-Зг

з у

" н

Ахфх + н

h 2 =

0

Ау

0

·

Фу

+

Зг

1

-Зх

·

0

=

Ау фу + НЗг

.          (2)

0

0

Аг

. фг_

.—Зу

Зг

1

0

. Аг фг + НЗу_

Зная кинетические моменты каждого тела. (1) и (2), применяя теорему об изменении кинетического момента, ко всему объекту управления и отделвно к парусу, получим

Г^(Һ 1 + ^Һ 2 ) + ш х ( h i + Һ 2 ) — М _5ИП, 1 Һ 1 + ш х Һ 1 — —к^С ц ,

(3а)

Q2 _ ^{(3 + г)} 2 ^2Q2 _ _{0 01} -2

^П ~ 2(1 +г) Д ^{2 П} ~ ^U‘^U1C

где к2С — эффективный коэффициент жесткости, к2 — ш2о

—

(см. Приложение). Пренебрегая моментами сил солнечного давления, M _stm, воздействующих на парус, получим следующую совокупноств уравнений:

{ Һ 1 + Һ 2 — const ,

Һ 1 + ш х Һ 1 — —к²Сц.

Расписывая систему уравнений покомпонентно, получаем уравнения движения объекта, управления вокруг осей Оу и Oz:

—A n ^z + С/І у + (С + Jy ) ф у + H3z — 0, А П ^у + С/г ₂ + (С + Jz ) ф z — НЗу — 0, —АП/г ₂ + СЦу + Сфу — А П ф _z — —tfCry , АП/г у + Cp z + Сфz + А П фу — —k^Grz .

(3c)

Полученную систему уравнений дополним законом управления: 3z — К1фу + К2фу + К з/ z у — вокруг ОСИ Оу II Зу — — ( K1фz + К2ф>z + К 3 /Іz) — вокруг оси Oz, где 3_z,3_у ~ угловые скорости прецессии ротора силового гироскопа вокруг соответствующих осей, Кі, К2, К3 — коэффициенты усиления обратной связи по состоянию, численные значения которых находятся из условий асимптотической устойчивости замкнутой системы, Ду, ц_z — оценки угловых скоростей колебаний мембранного диска паруса, полученных с помощью адаптивного наблюдателя [5].

Адаптивный наблюдатель применяется ввиду того, что переменные Ду и Д_z не могут быть измерены датчиковой аппаратурой. При проведении моделирования предполагалось, что оценки полностью соответствуют фактическим угловым скоростям колебаний л л ⁽Ду — /^у, ^г z — Д z )•

Из системы уравнений (Зс) следует, что стационарное движение при равномерной прецессии, например вокруг оси Оу, описывается следующими уравнениями:

( v- . ' + (С + Jy ) ф у ' + Н0?” — 0, ( АПф у^р — — к²С^ \

где фу^р — угловая скорость прецессионного движения вокруг оси Оу объекта управления (скорость программного разворота КА с вращающимся солнечным парусом), 3”^{Р —} установившийся угол отклонения вокруг оси Oz ротора силового гироскопа в подвесе Гука, обеспечивающий прецессионное движение КА, и г^^{р —} угол отклонения плоскости вращения паруса вокруг оси Oz при стационарной прецессии.

Решая систему уравнений (4) относительно г^Р с учетом выражения для к2, получим

Н

^ ^— .шкси) ^С (3+    ^,

АП + (С +Jy)А2(1+г) Д2П где г — 0.4 — коэффициент Пуассона материала мембранного диска.

Геометрическая интерпретация полученного соотношения отражена, на. рис. 3. Так как

Н — АП . то знаки г?' и 3”^р совпа.тают. а. 1^3 '| <  ІЗУ '|-

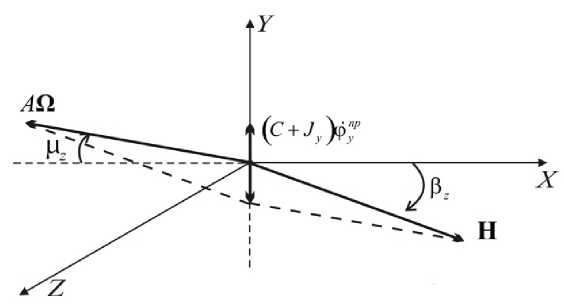
Рис. 3. Гиростатическая схема программного разворота вокруг оси Оу КА с солнечным парусом в установившемся режиме

4.    Расчетная схема математического моделирования

Рассмотрим систему уравнений, полученную при применении теоремы об изменении кинетического момента, для солнечного паруса.

Зная кинетический момент солнечного паруса, в проекциях на. связанные оси (1), применяя теорему об изменении кинетического момента, отделвно к парусу, а. также пренебрегая силами солнечного давления, воздействующими на парус, получим систему уравнений движения солнечного паруса вокруг осей Оу и Gz;

( —А П Ц _г + С Цу + С фу — А П ф _г = —к²Сцу , (АЮЦ у + С’^ + Сф, + А ^ фу — -к² С^ .

Учитывая соотношение между осевым и экваториальным моментами инерции паруса. (А = 2С), перепишем систему в следующем виде:

{ Цу — 2Qi _г + к ² Цу — —фу + 2^ф _z, 'i z + 2О.Ц у + к² iz — — фz — 2^ф у .

Вводя вектор состояния X( t ) — [ц_у(t) ц_у(t) ц (t) ц _z (t)]^T, запишем систему (6) в виде неоднородного матричного дифференциального уравнения: X (t) — AX (t) + F (t), где

0 1 0 0 0 A— —к2 0 0 0 0 0 2Q 1 , F(t) — —ф у + 2Qфz 0 0 —2Q —к2 0 _ — ф5 z — 2^фу_ неоднородного

Как известно, решение вид

уравнения через матричную экспоненту имеет

t

X (t) — e^A(t-to) X (to) + e A^ e^-A F( ^ ) d^. ^t0

Решая характеристическое уравнение однородной системы уравнений, получим собственные значения:

А2 + к2 2QA

—2QA

А2 + к2

— (А2 + к2 )2 + 4Q2A2 — А4 + 2(2Q2 + к2) А2 + к4 — 0,

А1,₂ — ±гш1, Аз,4 — ±гш₂, где ш1 — VQ² + к² — Q, ш₂ — VQ² + к² + Q.

Тогда, решение однородной системы уравнений выглядит следующим образом:

{ Д_у = A_i cos(w_it) + B_i sin(wit) + С_І cos( w₂t ) + D_i sin(w₂t), Д_г = В1 cos(w_it) — A_i sin(w1t) + D_i cos( w₂t ) — С_І sin(w₂t),

где Ai,Bi, Ci, Di — постоянные коэффициенты, которые находятся из начальных условий:

Ду(0) = Ду = Ai + С1, Дг (0) =Д° =Bi +D1, < /г у (0) = Ду = BiWi + D1W2, ^/7 г (0) = /70 = —AiWi — CiW2.

Ai = (/7 г + W2д0)/ ( w 2 — Wi), Bi =(—/7°+w2дг)/(w2—Wi),             (g) СІ = (—/7 ° — WiдУ ) / ( w 2 — Wi), _ Ai = (/7у — Wi7°)/ ( w 2 — Wi) -

Решение однородной системы уравнений X (t) = e^At X (0), где

е

At _

w ₂ — w_i

W2Ci — WiC2

— WiW2(Si — 82)

—W28i + Wi82

—WiW2(Ci — C2)

— Si + 82      W28i — Wi82       Ci — C2

—WiCi + W2 C2   WiW2 ( Ci — C2)   —Wi8i + W282

— Ci + C2      W2Ci — WiC2      —8i + 82

Wi8i — W282   —WiW2 ( 8i — 82)  —WiCi + W2C2

в обозначениях Ci = cos(w_it). C₂ = cos(w₂t). 8_i = sin(w_it) II 82 = sin(w₂t).

Чтобы найти решение неоднородной системы уравнений, найдем решение на. малом промежутке времени t Е [t°,t° + ^д], г де Һ — такт интегрирования разностного уравнения. После некоторых преобразований, считая, что F (£) = F (t) = const на малом интервале времени t. получаем

t

X(t) = eA(t-to)X(to) + eAt У е-A5F(£K = to eA(t-to) (X(to)+ F(t) — F(to)).

Таким образом, разностное уравнение, соответствующее неоднородному дифференциальному уравнению, будет

Х( п + 1) = e ^Ah (X( n ) + F (n + 1) — F (n)).

Перечисленная ниже совокупность уравнений полностью описывает расчетную схему математического моделирования динамического поведения космической платформы с вращающимся солнечным парусом.

—АПд_г + СД у + (С + Jy ) Д у + НЗг = 0,

АПду + СД г + (С + Л )д г — НЗу = 0, < X (n + 1) = e^Ah( X (n) + F (n + 1) — F (n)),

Зг = Ki Ду + К2фу + К3Ду, (Зу = —(KiДг + К2Д г + К3Д г ).

Моделирование проводилось в программных пакетах MATLAB 7.9.0 и Simulink. Блок-схема моделирования с параметрами модели представлена на рис. 4.

При математическом моделировании коэффициенты в законе управления скоростью прецессии силового гироскопа, в подвесе Гука, имели следующие значения:

Ki = 0.8c ^{- 1} , К2 = 3.6, Кз = 1.2.

Необходимо отметить, что исследования были проведены без учета естественного демпфирования колебаний мембранного диска, солнечного паруса, то есть рассматривался вариант активного демпфирования.

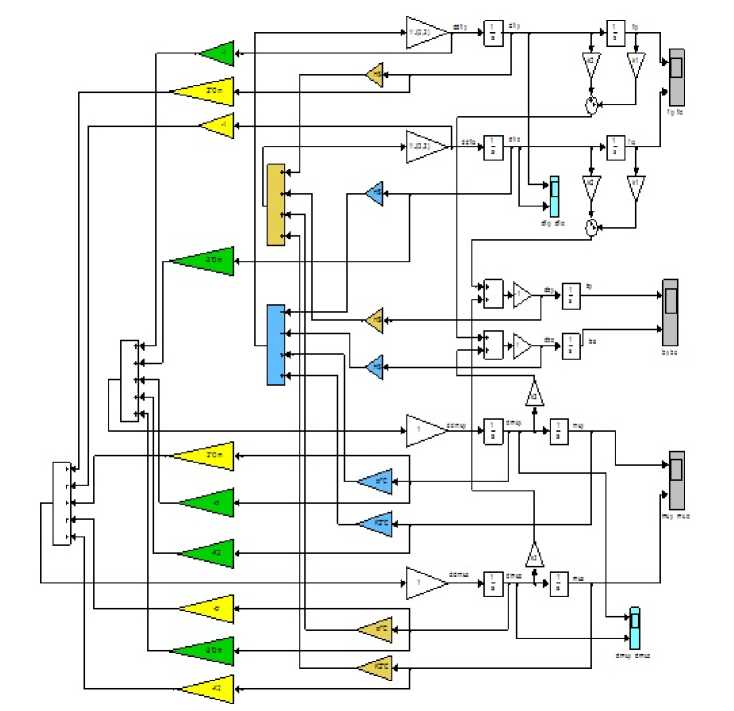
Рис. 4. Блок-схема, моделирования динамического поведения космической платформы с вращающимся солнечным парусом

5.    Моделирование режима демпфирования начальных угловых скоростей и режима программных разворотов

Динамическое поведение космической платформы с солнечным парусом в режиме гашения начальных угловых скоростей при активном демпфировании упругих колебаний мембранного диска, солнечного паруса, проиллюстрировано на. рис. 5.1-5.6. Для иллюстрации переходного процесса, на. рис. 6.1-6.6 приведены те же графики в увеличенном временном масштабе на. начальном этапе демпфирования.

Динамическое поведение космической платформы с солнечным парусом в режиме программных разворотов проиллюстрировано на. рис. 7.1-7.6. Для иллюстрации переходного процесса, на. рис. 8.1-8.6 приведены те же графики в увеличенном временном масштабе на. начальном этапе программного разворота.

В представленной реализации математического моделирования режима, гашения угловых скоростей значения начальных угловых скоростей вокруг осей Оу и Oz были заданы равными по 0.3 град/с.

При математическом моделировании режима, программного разворота, угол разворота, вокруг оси Оу был задан равным 90°. Скорость разворота принималась равной 0.06 град/с.

Из приведенных рисунков видно, что при выбранных законе управления и параметрах конструкции космической платформы с вращающимся солнечным парусом углы отклонения плоскости вращения мембранного диска, паруса, в режиме активного демпфирования не превосходят 1 градуса, а. в режиме программных разворотов со скоростью 0.06 град/с не превосходят 3.5 градуса. При этом во всех промоделированных режимах скорости прецессии ротора силового гироскопа в подвесе Гука не превосходят 1.5 град/с, а углы отклонения оси ротора не превосходят 3.5 градуса.

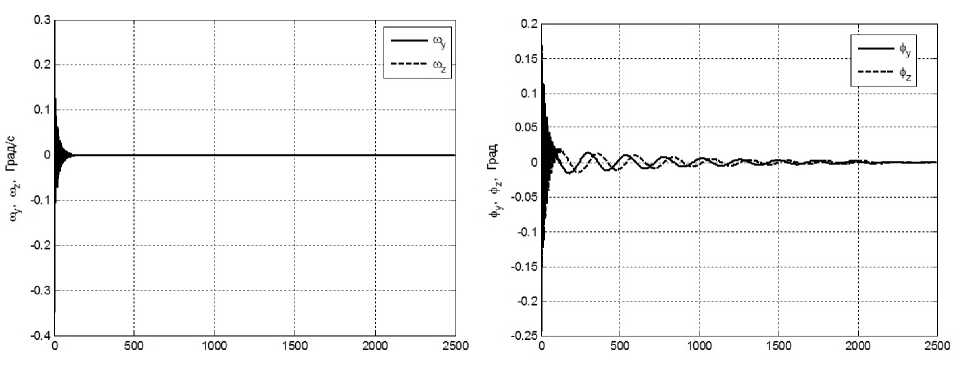
Рис. 5.2. Поведение угловых компонент положения КА вокруг осей Оу и Ох в режиме гашения

Рис. 5.1. Поведение компонент абсолютной угловой скорости КА вокруг осей Оу и Ох в режиме гашения

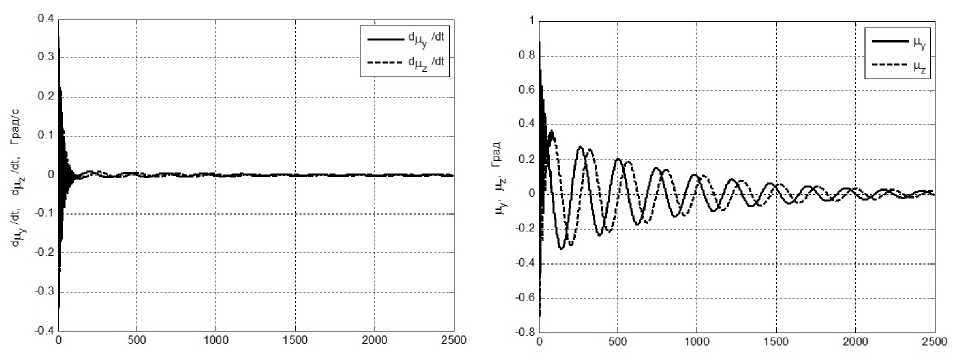
Рис. 5.3. Угловая скорость плоскости вращения солнечного паруса, относительно связанного базиса вокруг осей Оу и Ох в режиме гашения

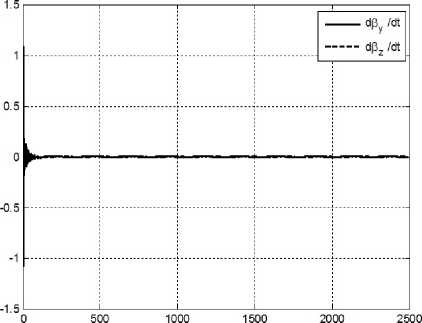
Рис. 5.4. Угловое отклонение солнечного паруса вокруг осей Оу и Ох в режиме гашения

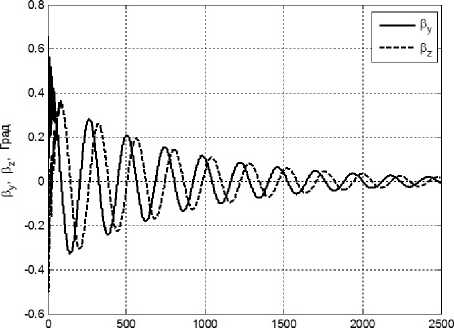
г г п                                   Рис. 5.6. Углы отклонения ротора, силового

Рис. 5.5. Скорости прецессии силового                                    L L гироскопа, в подвесе Гука, вокруг              гироскопа, в подвесе Гука, относительно осой Оу II Ох в режиме гашения            связанного базиса, вокруг осей Оу и Ох в режиме гашения

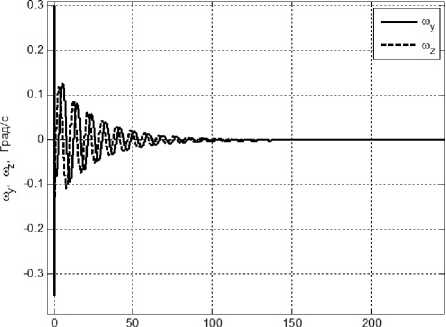
Рис. 6.1. Поведение компонент абсолютной угловой скорости КА вокруг осей Оу и Ох в

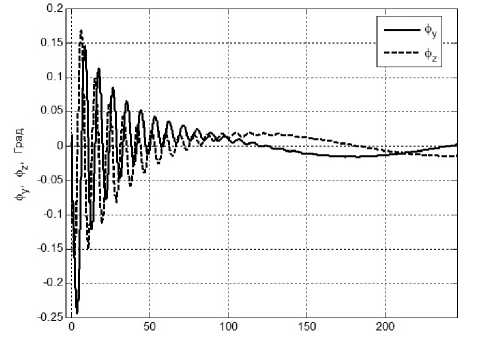
Рис. 6.2. Поведение угловых компонент положения КА вокруг осей Оу и Ох в режиме

гашения

режиме гашения

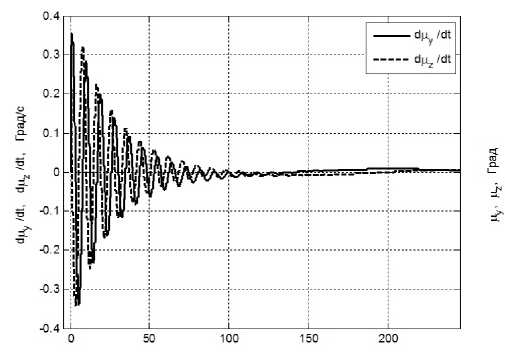
Рис. 6.3. Угловая скорость плоскости вращения солнечного паруса, относительно связанного базиса вокруг осей Оу и Ох в режиме гашения

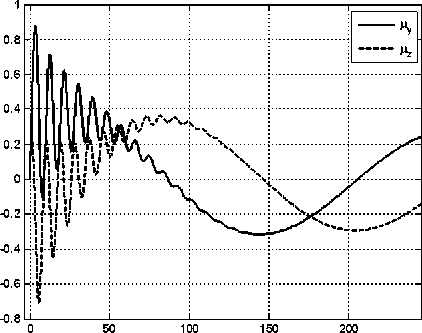
Рис. 6.4. Угловое отклонение солнечного паруса, вокруг осей Оу и Ох в режиме гашения

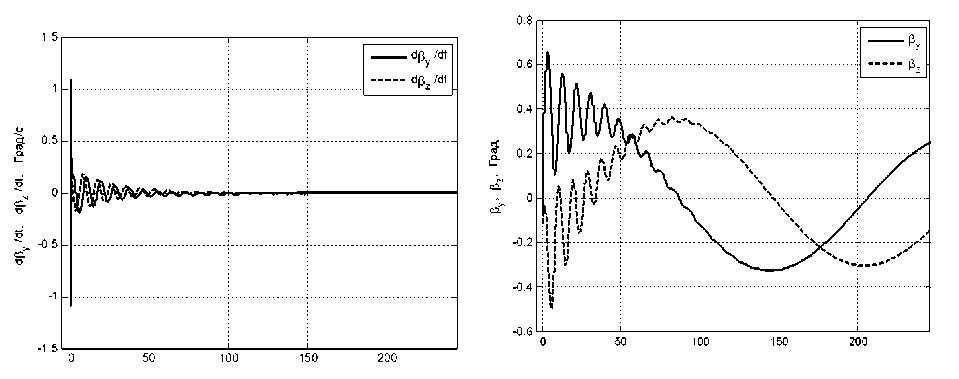
Рис. 6.6. Углы отклонения ротора, силового гироскопа, в подвесе Гука, относительно связанного базиса вокруг осей Оу и Ох в режиме гашения

Рис. 6.5. Скорости прецессии силового гироскопа в подвесе Гука вокруг осей Оу и Ох в режиме гашения

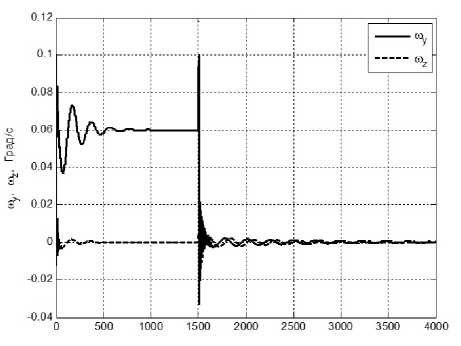
Рис. 7.1. Поведение компонент абсолютной угловой скорости КА вокруг осей Оу и Ох в режиме программного разворота.

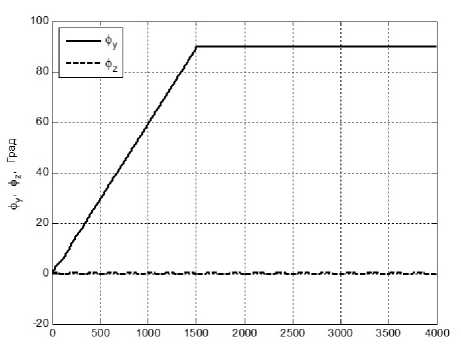
Рис. 7.2. Поведение угловых компонент положения КА вокруг осей Оу и Ох в режиме программного разворота.

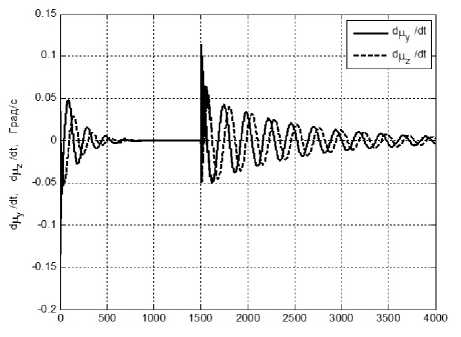
Рис. 7.3. Угловая скорость плоскости вращения солнечного паруса, относительно связанного базиса вокруг осей Оу и Ох в режиме программного разворота.

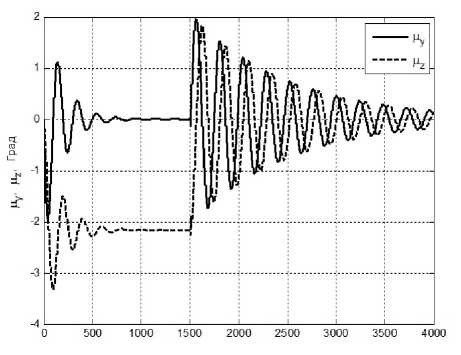
Рис. 7.4. Угловое отклонение солнечного паруса, вокруг осей Оу и Ох в режиме программного разворота.

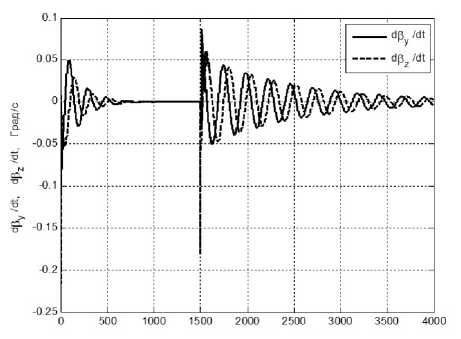
Рис. 7.5. Скорости прецессии силового гироскопа в подвесе Гука вокруг осей Оу и Ох в режиме программного разворота.

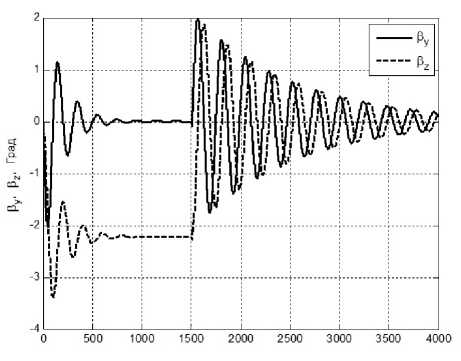
Рис. 7.6. Углы отклонения ротора, силового гироскопа, в подвесе Гука, относительно связанного базиса вокруг осей Оу и Ох в режиме программного разворота.

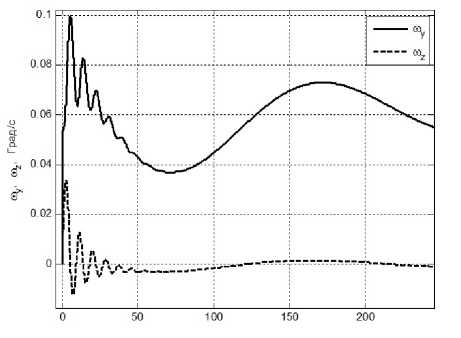
Рис. 8.1. Поведение компонент абсолютной угловой скорости КА вокруг осей Оу и Ох в режиме программного разворота.

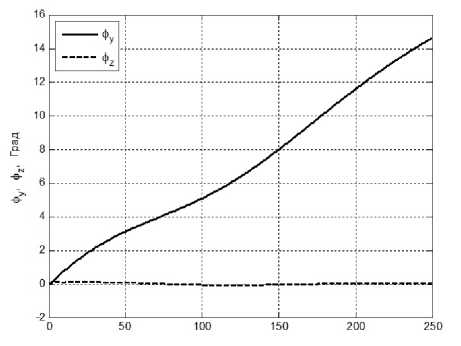
Рис. 8.2. Поведение угловых компонент положения КА вокруг осей Оу и Ох в режиме программного разворота.

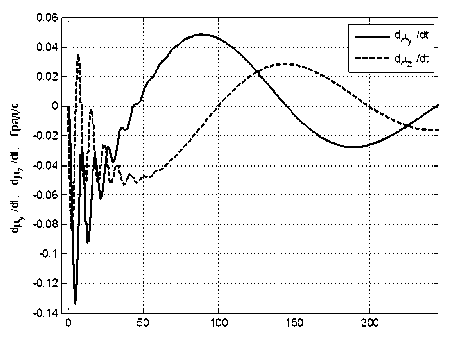
Рис. 8.3. Угловая скорость плоскости вращения солнечного паруса, относительно связанного базиса вокруг осей Оу и Ох в режиме программного разворота.

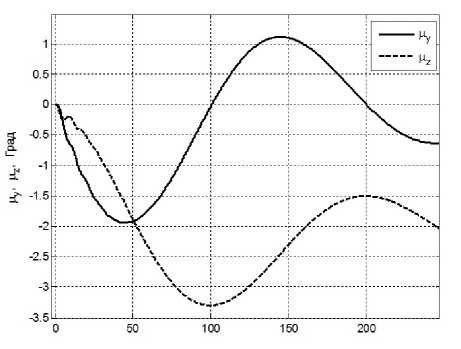
Рис. 8.4. Угловое отклонение солнечного паруса, вокруг осей Оу и Ох в режиме программного разворота.

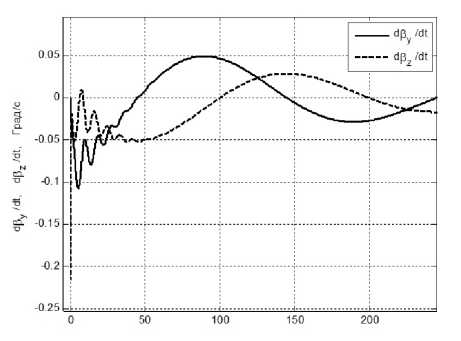
Рис. 8.5. Скорости прецессии силового гироскопа в подвесе Гука вокруг осей Оу и Ох

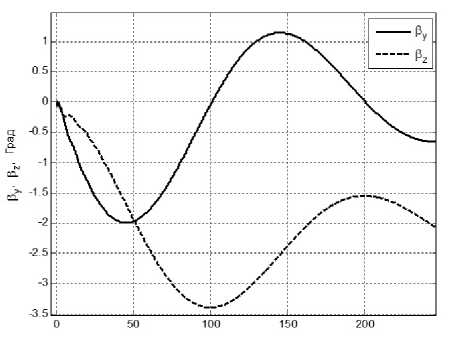
Рис. 8.6. Углы отклонения ротора, силового гироскопа, в подвесе Гука, относительно связанного базиса вокруг осей Оу и Ох в

в режиме программного разворота.

режиме программного разворота.

6.    Заключение

На основе полученных фундаментальных результатов [1, 2], позволяющих преодолеть сложности в описании динамического поведения космического аппарата как объекта управления с распределенными параметрами в процессе выполнения им угловых маневров, а. также позволяющих представить поведение вращающегося мембранного диска, с центральной жесткой вставкой в виде гироскопа, в упругом подвесе со своей приведенной жесткостью крепления подвеса, и приведенным кинетическим моментом, разработана, математическая модель динамики вращающегося мембранного диска, с центральной жесткой вставкой.

С целью подтверждения правильности выбранной концепции построения космических платформ с вращающимся солнечным парусом, выбора, основных параметров базовой конструкции платформы и проверки разработанных алгоритмов управления ее движением было проведено математическое моделирование динамического поведения объекта, управления в режиме гашения начальных угловых скоростей при активном демпфировании упругих колебаний мембранного диска, солнечного паруса, а. также в режиме программных разворотов.

Моделирование реализовано в программных пакетах MATLAB 7.9.0 и Simulink. Анализ результатов моделирования подтвердил правильность выбранной концепции конструкции космической платформы, а. также законов управления движением.

В дальнейшем при описании динамического поведения КА с большим вращающимся солнечным парусом в режиме развертывания мембраны предполагается учесть колебания полотнища, вокруг продольной оси аппарата, (ось вращения паруса).

Работа, выполнена, при финансовой поддержке Российского фонда, фундаментальных исследований (12-08-00254-а).

7.    Приложение

Уравнение возмущенного движения солнечного паруса, во вращающейся системе координат Ox'y'г' , жестко связанной с центральной вставкой, имеет вид

£ (Vr^) + д f ^ dW^ = pr^ + 2- L;pr2 cos(y + Ot) + dr у dr у dy у r dy у      dt2                                  (П .1)

+ шуpr2 sin(y + Ot) + 2Owzpr2 sin(y + Ot) — шzpr2 cos(y + Ot), где W(r,y,t) - поперечное смещение точки мембраны, а аг и и^ - радиальное и тангенциальное напряжения [1]. Краевые условия имеют вид W(a,y,t) = 0 и W(r, y, t) - ограничено при r ^ R — 0.

Собственные формы соответствующей краевой задачи были вычислены в [1] и выглядят соответствующим образом:

Vnk ( r, y) =

^^nfc ^(r) V ^Inkh

cos ny,

Vnk (r, ?) =

Дш „(r)

^n/c

V ^kkh

sin ny,

где w_nk ~ собственные частоты; l_nk ~ нормирующие коэффициенты; явное выражение Кш_пк (r) через функции Хейна F ( a,q,a, 3,^,6, г) приводится в [1, 6].

Ищем решение уравнения (П.1) в виде ряда, по собственным функциям

∞∞

W ( r,y,t ) = ЕЕ [qnk(t) Vnk ( r, y ) + Snk ( f ) Vnk ( r, y)] ,              (П.2)

n=0k=0

где q_nk и s_nk — обобщенные координаты.

Подставляя (П.2) в (П.1) и сравнивая коэффициенты при собственных функциях в левых и правых частях, получим уравнения

{ q ik (t) + w2_kqik (t) + aik [(2Ошу — ш_г) cos Ot + ( Шу + 2Ош_г) sin Ot] = 0, Sik(t) + w²_ksik (t) + aik [(Ш_г — 2O wy ) sin Ot + (Шу + 2Oш_г) cos Ot] = 0,

(П .3)

где “_nk — коэффициенты Фурье разложения функций г cos д и г sin д по системам {V_nk } и {V_nk } соответственно. (При п = 1 коэффициенты “_nk равны нулю, поэтому в уравнениях (П.З) рассматривается только случай п = 1).

Если обозначить tik = -qik + isik, уравнения (П.З) записываются в виде одного комплексного уравнения:

tik + ш2кtik + “ik [iz - 2Qiy + i ( iу + 2Qiz)] е^ — 0.              (П.4)

Само решение в терминах комплексных коэффициентов запишется как

∞

W (г, д,t) = - ReV .-tik(t).                      (П.5)

k=o V ^h

В уравнении (П.4) неоднородность является сильно осциллирующей, поэтому целесообразно сделать замену tik — t^e^zQt. Нетрудно видеть, исходя из (П.5), что эта замена соответствует переходу от вращающейся системы координат к приборной, то есть если ^tik = -ik ^{+ is}ik- ^то

∞

W(г, д, t) = - Re £ k=0

^Ргще e^^ik^(t) = £ [^qik^{(t) cos} Д ^{+ s}ik^{(t) sin} Д] ^^ГЩ)

V Mikh          k=0                        V'ikhh будет разложением по собственным функциям в приборной системе координат (при этом полярные углы во вращающейся системе координат и в приборной отличаются на Qt).

Итак, производя в (П.4) указанную замену и отделяя действительную и мнимую части, получаем уравнения на. обобщенные координаты в приборной системе координат:

f qik(t) + 2QSik(t) + (i2k - Q2)^ik(t) + “ik (2Qiy - ^z) =

(П .6)

1 Sik(t) - 2Qqik(t) + (i2k - Q2)si k(t) + “ik (iy + 2Q^z) =0.

Моменты, действующие co стороны мембраны на. жесткую вставку относительно осей Оу и Oz, вычисляются по формулам

Му = - £ “ikS'ik(t) + 2Q 5 “ikHik(t) - C(ciу + 2Q^z), k=0k=0

Mz = £ “ikqik(t) + 2Q 52 “ikS’ik(t) - c(ciz - 2Qiy), k=0k=0

где C — экваториальный момент инерции мембраны.

Так как моменты, создаваемые мембраной, должны быть противоположны моментам, действующим на. жесткую вставку со стороны остальной части КА (тело 2), и переход от обобщенных координат к физическим производится по формулам /zk = -^М- и /yk = -k^-1 “ik          “ ik то получаем следующую совокупность уравнений:

'c(ciy + 2Q iz ) + ЕГ=о “i k [/iyk(t) - 2Q ^zk (t)] = M™ ^сш, _< C (ciz - 2Qiy) + E^=o “i k [/zk(t) + 2Q/yk (t)] = M™ ^еш, ^zk ^{(t) - 2Q/}yk ^{(t) + (i}2k ^{- Q2)}/zk^{(t) +} ^ⁱ z ^{- 2Qi}y = 0, J^yk ^{(t) + 2Q}/^ zk ^{(t) + (i}2k ^{- Q2)}/yk^{(t) + ci}y ^{+ 2Qi}z = 0.

Данная система напоминает систему уравнений движения гироскопов в упругом подвесе. Поэтому /yz и /zk приобретают физический смысл углов поворотов гироскопов относительно соответствующих осей.

Отсюда можно сделать вывод, что коэффициенты “ik характеризуют степень участия тонов в движении мембраны как твердого тела, а Е/Ео “2k = C, поэтому по процентному вкладу Q2fc в момент инерции мембраны можно судить о важности учета отдельно взятого тона, в данной математической модели мембраны.

В реальности при обычных параметрах мембраны ( a/R = 0,1 ид = 0,4) приведенные моменты инерции первых двух гироскопически связанных мод движения (а2о) дают 99,9% от моментов инерции мембраны как твердого тела. Поэтому математическая модель упругой мембраны сводится к модели одного гироскопа, в упругом подвесе. При желании можно учитывать и большее число гироскопов.

Таким образом, усеченная модель динамики мембраны с центральной жесткой вставкой с учетом а2о ~ С может быть описана следующей системой уравнений:

( ш, ₊ 2Пш , + д , (,) ₊ 2Яд . (t) = 1^,

С

Ц. - 2^ + д(t) - 2»д , (t) = 1^,                     (ПЛ)

Дг (t) — 2ПД, (t) + (ш20 — П2)дг (t) + ш z — 2Пш, = 0, д, (t) + 2Пд z (t) + (ш2о — П2)д, (t) + ш, + 2Пшг = 0, где д, = д,о, дг = дго.

По виду уравнения (П.7) напоминают уравнения (Зс) из основного текста. Более детальный вывод уравнений можно найти в [1, 2].