Исследование динамики захвата гильзы валками пилигримового стана
Автор: Раскатов Е.Ю.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Общие проблемы машиностроения
Статья в выпуске: 1-3 т.13, 2011 года.
Бесплатный доступ
Описана методика расчета максимальных динамических нагрузок в линии привода пилигримового стана при мгновенном приложении нагрузки.
Пилигримовая прокатка, алгоритм, энергоёмкость, математическая модель, динамический момент, расчетная модель
Короткий адрес: https://sciup.org/148199688
IDR: 148199688 | УДК: 621.771.06-589.4
Текст научной статьи Исследование динамики захвата гильзы валками пилигримового стана
одной трубы) и др. На пилигримовых станах производят трубы весьма широкого сортамента и практически любого назначения: трубы нефтяного сортамента, обсадные, баллонные, котельные, трубы из специальных сталей и сплавов, биметаллические трубы разных сочетаний (для АЭС и для транспортировки сыпучих абразивных материалов), трубы спецна-значения для ВПК. Эти преимущества дают основание считать, что способ пилигримовой прокатки труб еще долгие годы будет успешно конкурировать с другими способами производства труб.
Бесшовные трубы диаметром более 406 мм с разными толщинами стенок без применения специального оборудования (гидравлических прессов и станов расширителей) можно производить только на ТПУ с пилигримовыми станами. Экономичность производства труб малыми партиями (до одной трубы) также следует отнести к достоинствам установок с пи-лигримовыми станами. Об этом также свидетельствует анализ технико-экономических показателей различных способов производства стальных труб [1]. При пилигримовой прокатке бесшовных труб цикл деформации гильзы периодически осуществляется за один оборот валков с переменным радиусом калибра, причем направление вращения валков противоположно направлению подачи гильзы. При этом особенно важно оценить условия захвата металла валками, закономерности формирования мгновенного очага деформации, и изменения скорости перемещения гильзы, а также уровень динамических нагрузок в линии привода пилигримового стана. Уравнение движения гильзы при её захвате имеет вид:
G dVr 2 g dt
= n R 2 5 ( т cos a - g sin a ) kn
где G – вес гильзы и дорна, кН; V r – скорость перемещения гильзы, м/с; R – переменный радиус бойковой части валка, м; δ – дуга соприкосновения металла с валками, рад; τ k – касательное контактное сопротивление, МПа; σ n – нормальное напряжение, МПа; α – угол захвата, рад.
Скорость гильзы и угол δ связаны зависимостью [2]:
d S
V r = R cos a —; dt
Подставив зависимость (2) в уравнение (1) по лучим дифференциальное уравнение для δ:
где dS1 dt2
+ Pi 5 = 0
12 g ( ^ n tg a - T k )
G
Общее решение уравнения (3) имеет вид
δ = с 1 sinβ 1 t + c 2 cosβ 1 t
Начальные условия : t=0, δ=0, dδ/dt=ω 0 , где ω 0 – угловая скорость валка , 1/ с . С учетом началь ных условий зависимость для определения ду ги соприкосновения металла с валками прини мает вид :
5 = ^°sin Pt(5)
Pi отсюда dS
— = dt 01 С учетом (6) зависимость для определения скорости гильзы принимает вид: Vr = R cosα ω0 cosβ1t(7) Расчет параметров механической системы пилигримового стана показал, что отношение массы якоря двигателя и маховика к суммарной массе системы, которое называют коэффициентом распределения масс, близка к единице. В связи с этим амплитуда колебаний якоря и маховика в десятки раз меньше амплитуды колебаний валка, а переходный процесс захвата гильзы валками может без больших погрешностей рассматриваться как упругие колебания приведенной массы валка относительно якоря двигателя и маховика, вращающихся с постоянной скоростью. Для одномассовой расчетной модели дифференциальное уравнение движения валка при наличии упругой связи в переходной стадии захвата имеет вид: J ip + cp = -nR 35тк (8) где J – момент инерции валка, т·м2 (кН·м·с2); φ - угол поворота валка, рад; p - угловое ускорение валка, с-2; c – жесткость упругой связи, кН·м. Подставив δ из (5) в уравнение (8) получим: o ic nR 3T^-2 P = ; с 1; h =—, N J Jp1 Общее решение дифференциального уравнения (10): ф = с1 cos pt + c2 sin pt + h P2— Pi2 sin p1t С учетом начальных условий: t=0, ф=0, & = 0 , решение уравнения (10) принимает вид: Ф = h P2 — Pi2 sin Pi t — ^sin Pt I P 7 Динамический момент крутильных колебаний MД = —9c^ 9 sin Pt -—sin Pt P2- Pi I P Исходные данные для расчета, результаты расчета на рис. 1: ω0 = 4,72 c-1, Rc = 0,27 м, J = 0,7 тм2, с = 9000 кН м, α = 15о, σn = 105 МПа, G = 1,87 +1,66 = 3,53 т, β = 113 1/с, β1 = 9,7 1/с, h = 1230 c-2, MД = 520 кН м. Рис. 1. Зависимость максимальной амплитуды динамического момента от жесткости шпинделей пилигримового стана Вывод: на основе теоретического исследования динамики захвата гильзы валками пи-лигримового стана разработана методика рас- 1. чета максимальных динамических нагрузок, 2 возникающих в линии привода пилигримового стана, при мгновенном приложении нагрузки.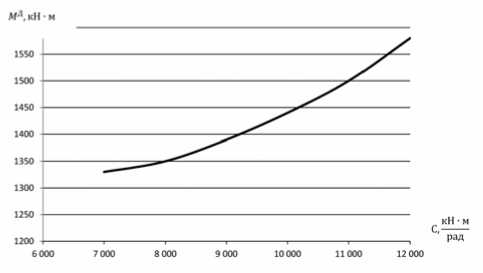
Список литературы Исследование динамики захвата гильзы валками пилигримового стана
- Тетерин, П.К. Теория периодической прокатки. -М.: Металлургия, 1978. 256 с.
- Лехов, О.С. Динамические нагрузки в линии привода обжимных станов. -М.: Машиностроение, 1975. 184 с.
- Чечулин, Ю.Б. Измерение нагрузок на шпинделях валков пильгерстана/Ю.Б. Чечулин и др.//Металлург. 2007. №6. С.47-49.


