Исследование дискретных преобразований Уолша-Адамара в обработке результатов

1. Преобразование Уолша-Адамара

Преобразование Уолша-Адамара - это ортогональное преобразование, которое разделяет сигнал на набор ортогональных прямоугольных волновых форм, называемых функциями Уолша. Преобразование

не имеет множителей и является вещественным, поскольку амплитуда функций Уолша имеет только два значения, +1 или -1. Простейшей матрицей Адамара является матрица второго порядка, имеющая вид:

H 2 =

-1

Пары дискретного преобразования Уолша-Адамара в показательной форме показано в таблице 1.

Преобразование Уолша-Адамара может использоваться во многих различных анализах, таких как анализ спектра мощности, фильтрация, обработка речевых и медицинских сигналов, мультиплексирование и

кодирование в связи, определение характеристик нелинейных сигналов, решение нелинейных дифференциальных уравнений, логическое проектирование и анализ.

2. Базис Уолша-Адамара

Таблица 1. Дискретные преобразования Уолша-Адамара в показательной форме

Прямого преобразования	Обратного преобразования	Преобразования в матричном виде
N - 1 b ( к )   2 5 ( ” )( - 1) k” , n = 0 к = 0,1,..., N - 1	N - 1 s ( n ) = N - | 2 b ( к )( - 1) к ” , к = 0 n = 0,1,..., N - 1	B = HS s = N-1 HB

В матрице Уолша-Адамара функции Уолша располагаются в таком порядке, что их отсчеты образуют матрицу Адамара. Это означает, что систему Уолша-Адамара можно синтезировать, основываясь на известных свойствах этих матриц. Матрица Адамара второго порядка представлена в формуле (1).

Поскольку дискретная частота играет роль номера функции в базисе, а дискретное время - аргумент базисной функции, то для упрощения дальнейших записей введем следующее обозначение для фазовращающего множителя:

—

W = е А 2 J = е 7^ = —1 (2)

то матрицу H2 можно записать в виде г W0  W"l,,,

^H 2 = [W »   W 1 ] ⁽³⁾

При N = 2 2 = 4 элементами матрицы H 4 Адамара станут матрицы H 2 :

^н 4 = [^н 2

н2

—^Н 2

Г0  0  001

1    0  1  0

]   0 011

L 0   1  10J

Видно, что при увеличении параметра n на единицу количество строк матрицы Адамара удваивается, так же, как и коли-

чество элементов в каждой из них. Для любого двоично-рационального порядка выполняется следующее равенство

H₂ ”+i = RJ² ”    ^Hf ](5)

• ²     LH 2 ” — Н 2Ч

Используя матрицу (4) синтезируем матрицу Адамара восьмого порядка Н₈ :

	0	0	0	0	0	0	0	0
	0	1	0	1	0	1	0	1
	0	0	1	1	0	0	1	1
н8 =	0	1	1	0	0	1	1	0	(6)
	0	0	0	0	1	1	1	1
	0	1	0	1	1	0	1	0
	0	0	1	1	1	1	0	0
	-0	1	1	0	1	0	0	1-

Сформулируем некоторые свойства полученной матрицы: Она является симметричной. Это означает, что все выводы относительно ее строк можно применить и к ее столбцам. Каждая строка этой матрицы, за исключением нулевой, состоит из равного количества нулей и единиц. Нулевая же строка изоморфного отображения матрицы Уолша-Адамара любого порядка состоит из нулей. Равенство всех элементов первой строки нулям и одинаковое количество нулей и единиц во всех остальных строках являются особенностями не только системы Уолша-Адамара, но и любой другой системы Уолша. Анализируя матрицы приходим к выводу о том, что для первой функции в матрице Адамара любого возможного порядка выполняется равенство:

^ 1

( +1, для четных I

I-1, для нечетных I

• 3.    Обработка ЭКГ-сигналов

Часто возникает необходимость записывать сигналы электрокардиограммы (ЭКГ) пациентов в разные моменты времени. В результате образуется большой объем данных, который необходимо сохранить для последующего анализа и сравнения. Преобразование Уолша-Адамара подходит для сжатия ЭКГ -сигналов, поскольку обладает такими преимуществами, как:

• 1)    Быстрое вычисление коэффициентов Уолша-Адамара;

• 2)    Меньший объем памяти, поскольку достаточно хранить только те коэффици-

• енты последовательности, которые имеют большие значения;

• 3)    Быстрое восстановление сигнала.

Ниже приведена оценка ЭКГ-сигнала и соответствующего ему преобразования Уолша-Адамара. При тестировании системы рассматривалась одиночная волна ЭКГ-сигнала, равная 512, который зашумлялся при помощи АБГШ. Так же для обработки данных использовалось быстрое преобразование Уолша-Адамара. Результаты моделирования представлены на рисунке 1.

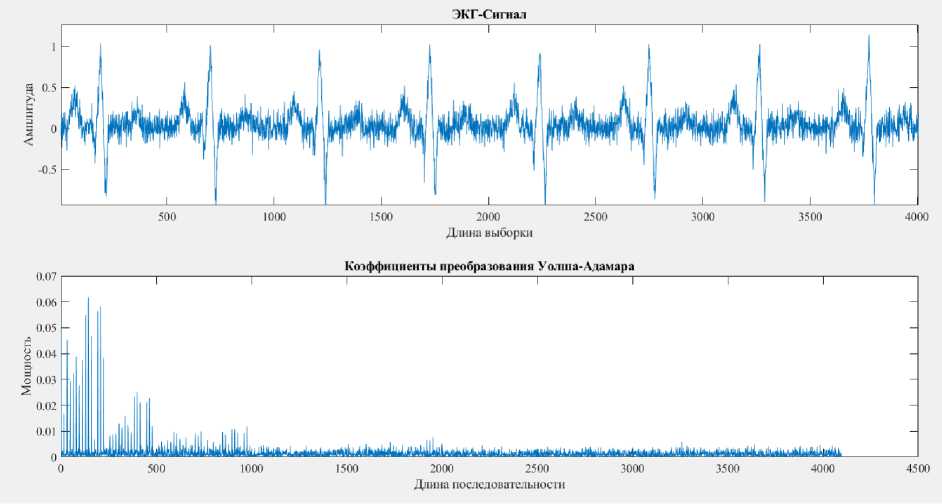
Рис. 1. Исходный ЭКГ-сигнал и полученный сигнал при использовании быстрого преобразования Уолша-Адамара

Как видно из рисунка 1, большая часть энергии сигнала сосредоточена в нижних значениях последовательности. Для целей исследования сохраняются только первые 1024 коэффициента, которые используются для восстановления исходного сигнала.

Усечение коэффициентов более высокой последовательности также способствует подавлению шума. Оригинальный и восстановленные сигналы показаны на рисунке 2.

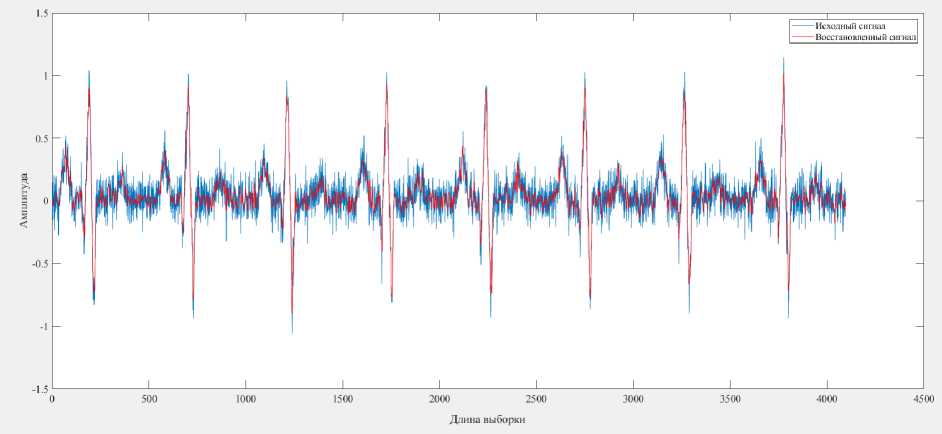
Рис. 2. Оригинальный и восстановленный сигнал

По результатам моделирования видно,    первые 1024 коэффициента и длину сигна- что восстановленный сигнал очень близок   ла ЭКГ, что соответствует степени сжатия

• к исходному сигналу. Чтобы восстановить примерно 4:1.

исходный сигнал, мы сохранили только