Исследование донных линий потока при развороте потока

Значительный круг задач, рассматривающих течение рабочего тела в проточной части лопаточных машин, связан с необходимостью интегрирования уравнений пограничного слоя по сложной криволинейной поверхности с поперечным градиентом давления. Наиболее верные и продуктивные шаги в этом направлении были сделаны Г. Ю. Степановым [1] и С. Н. Шкарбулем [2], построившим свои гипотезы на анализе сил, действующих на элементарный объем жидкости при повороте. Однако отсутствие обоснования коэффициентов Ламе для рассмотрен-

терные толщины ППС) [1], которые для практических расчетов в безотрывной зоне считаются постоянными величинами:

*

н = ^, 8 **

ф

**

L = 4

2   **

^{£ 8} ф

8 **

I _^v

*ф*

,

*

K=-^L K о** , ^£8 ф

ных ими каналов, а также то, что ядро потока принимается потенциальным (безвихревым), не дает возможности адап-

тировать уравнения для случая произвольного закона распределения скоростей и давлений в ядре потока. Для эффективного выбора метода решения и построения расчетного алгоритма необходимо привести систему уравнений импульсов пространственного пограничного слоя (ППС)

к виду, определенному по переменным и позволяющему

вести как численное, так и аналитическое интегрирование.

Общий вид уравнений пространственного пограничного слоя [3] в естественной системе координат

1 55_ф 1 5 И            гЛ

--— +--28л + 8^-8 + нф дф   нфи дф ( ф ф )

+д8 Фк₊ U _х н , «V   H , U д»

* ( 2 ⁸;-⁸ , ) + -nV ^н ( ^{2 8}ф; - ⁸; ) = H ф H V ^д»

¹    д р ₈,2 о^

Р н ф и ² дф   Р и ^2,

1 «8 » + X Хк ₊ 2 8 "ф д U + н » д» н ф дф   н ф и дф

₊ 2 8 »* д и ₊ 2 8 »ф д н » ₊ н » и д» н ф н » дф

**

, M = ¹

**

^{£ 8} ф

,

N = —, 8 ** ф

где 8 ф* - толщина потери импульса в направлении <р (вдоль т ₀ »

линии тока); £ = tg O 0 =---- тангенс угла скоса донной

**     **    ** Т0ф линии тока; 8ф», 8»*, 8»*ф - характерные толщины потерь импульсов; 8ф, 8» - толщины вытеснения в проекциях на оси естественной системы координат (продольной р и поперечной »); 8ф, 8» - толщины ППС в проекциях на оси естественной системы координат [3].

В естественной системе координат координатная линия р совпадает с проекцией предельной линии тока на стенке, а координатная линия » ортогональна р . Дифференциал дуги координатной линии равен дифференциалу по аргументу dS_i = H_idq_i , следовательно в естественных координатах, привязанных к известным линиям тока, коэффициенты Ламе н _р = н » = 1. В результате преобразований получаем систему из двух уравнений с двумя неизвестными:

д8 **       д8 **         ds

—+ I £^^ + 1 8ф—= дф     д»    ^ф д»

_Х« p 8" -(2 + н - N ^х

Р и ² дф ^{ф v} ’ и дф

-(2 1 - K )^£8^^{д и} + т(и ; 8 ** ; у)

⁽      ) и д» ^{( ф} )

д8* *         д8 **

M £^^L + L £ ²    +

дф      д»

-

,

д н

+--^Х*+8**+8*-8) = нн д» ( » ф ф )

+ M 8 **— + 2 L 8 **£— = ^ф дф ^ф д»

- 1 д р     ^т o v

Р н V и ² д»   Р и²

N д р 8» + ² L ^£ 2 ⁸ ф* д и + Р и ² д» ^ф и д»

не позволяет провести интегрирование, поскольку число неизвестных функций здесь превышает число уравнений.

Воспользуемся известным приемом и введем относительные существенно положительные величины (харак-

2 M £8 ф* д и

++ и дф

£ T ( и ; 8 ф* ; v )

где принятый закон трения T ( и ; 8 ф* ; v ) = Ц ф ₂ . Для тур-

булентного распределения скорости

U- = I У ) ⁷ и (зJ закон трения записывается в виде [5]

/               X Т 2

т ( и ; 3 ф*; v ) _р'

I и 3 ** = 0,01256 —^L

-0,25

-

Система (2) принадлежит к виду квазилинейных дифференциальных уравнений в частных производных [4]. Дискриминант характеристического уравнения (2) имеет вид

D = 4 L £ ²( 5 ф* )² ( L - MI ) , следовательно эта система относится к эллиптическому, параболическому или гиперболическому типам, если величина L /( MI ) меньше, равна или больше единицы соответственно. Для различных профилей скорости эта величина близка к единице [ 1].

В случае параболичности у системы уравнений импульсов (2) существует одно семейство характеристик

X- *- I = , d ф

а дифференциальное соотношение на характеристике имеет вид

, . d ^£      .

M— = - MN

d ф

N д p

£ д p p U ² дф

р U ² дф

KM £ ² д U

- ( N - Я ) Ml ^д и ^v ’ и дф

U дф

( M + 1)jr т ( и ; 3 ф* ; v ) . з _ф

Во многих случаях потенциального течения в ядре потока удобнее использовать несколько упрощенную запись уравнений импульсов (2) и дифференциального соотношения (5).

Во внешнем безвихревом потоке

1 д p = и д и - 1 д p = и д и р дф дф    р дф дф

-

Подставим эти выражения в (2) и (5) и получим уравнения импульсов ППС в случае потенциального ядра потока

д3Г     де :*        д^£

+ I £^-+ 1 3ф*—^£ дф     дф    ^ф дф

^{-( 2 +} H )Ц ^{-( 2} I ^- K )

**

£3 _ф д и ^хяг^+ ^т ( ^и ; ³ф ; ^v )

U дф ''

д3**

M£—+ L£2

,

дф

дф

Яр         Яр

+ M 3 **— + 2 L 3 **£— = ^ф дф      ^ф дф

d £ MH £ д и /        ₂Х

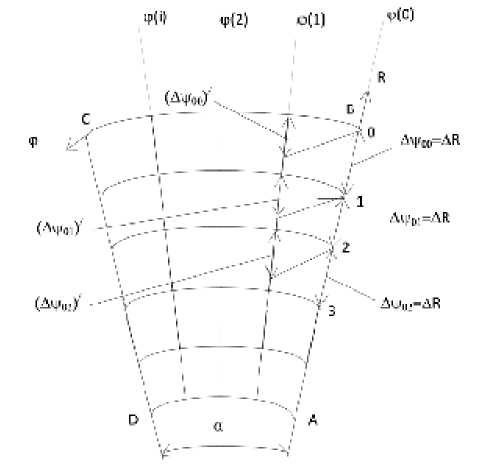
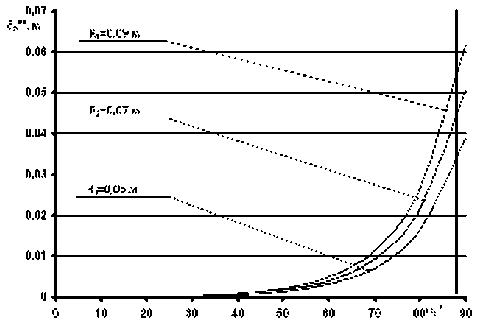
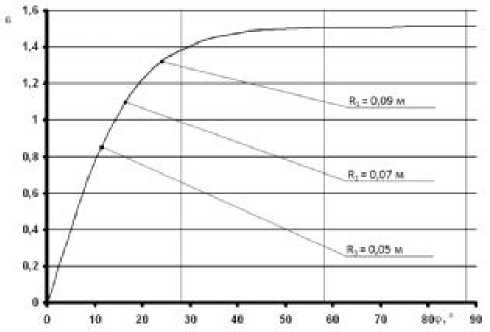
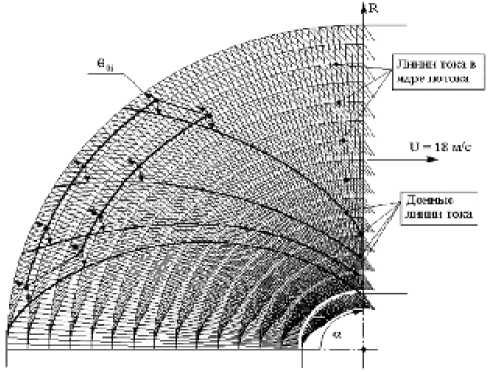
M — =--+ N - KM £ х d ф U дф v ’ х U 1ф-

где £ - тангенс угла скоса донной линии тока, £ = tg 00.

Дифференциальное уравнение (7) выражает зависи-

**

мость £ от ф и 3ф вдоль характеристик.

Для потенциального течения в круговом секторе сделаем некоторые допущения. Скорость потока вдоль линии тока не изменяется:

^ди = 0.

дф

Распределение скорости по радиусу подчиняется закону свободного вихря UR = C, тогда ди = д U = - d | C^ = 2 C дф = дR ” dR (R J= R2 .

Для решения используем комбинированный метод, совмещающий метод конечных разностей и метод характеристик. Система уравнений записывается в конечных разностях с учетом принятых выше допущений и включает уравнение характеристик

Аф = I £Аф = I £RAa,              (8)

дифференциальное соотношение на характеристике

А£ = Я

£ AU ,..₂х 1 AU --+ N - KM £-- и Аф         ’ MU Аф

M +1 £

M 3ф* и уравнение импульсов

T (-; ³ф*; v) ^Аф

**                              **

A3** = (K - 21) f-A^^ - (2 + Я) f^^AU + ^{ф (}      ) U Аф ⁽     ) U Аф

/         X     A3**

+T (U; 3ф*; v)-I £— v ф 7     Аф

I3** — Аф ^ф Аф

Численное интегрирование выполняется следующим образом (рис. 1).

В области решения ABCD определяются поля скоростей, линии тока и строятся естественные координаты ф и ф. На входе в область (кривая АВ) задаются значения £₀ и (5ф )₀. По выражению (8) находятся точки пересечения характеристик, выходящих из узлов в плоскости ф(0) с плоскостью ф(1): Аф₀₀, Аф₀₁, Аф₀₂,.... Отметим, что эти точки не совпадают с узлами на линии тока в плоскости ф (1) (см. рис. 1).

По выражению (9) определяются приращения вдоль каждой характеристики:

^А£00, ^А£01, ^А£о2^,.

.. .

Значения £ в плоскости ф(1) находятся по выражениям (^£10 ) = ^£00 ^+А£00’ (^£11 ) = ^£01 ^+А£01’

(2L£²- N+ '         ' и дф

2M£3** Эи     / х

+-------- + £ T U; 3**; v)

_ и дф ^{( ф}) и дифференциальное соотношение

(^£12 )    ^£02 ^{+ А£}02 ’ .

.. .

где обозначения для £ взяты со штрихом, поскольку точки пересечения характеристик с плоскостью ф(1) не совпадают с узлами.

Затем делается допущение о гладкости функции £(R) (или £(ф)), после чего выполняется коррекция значений,

т е. определяются значения = непосредственно в узлах:

=1о =-----(^) "*Е")-----; (AVoo )' + (=„)',

AR _(Ay 00 ) +(AVoi )

=11 =-------'' ' '■ )-------г(4V«)' +(=11)'

AR _(AVo1) +(aVo2 )

Рис. 1. Схема численного интегрирования

Приращение толщин потери импульса вдоль координатной линии ф (y = const) рассчитывается по выражению (10). Поскольку

А __< dyd то разностные аналоги производной имеют вид

**         c** c**

^Л5Ф I _Ao A

AR I       AR’

**          ^** e**

Л5Ф I _A -A AR I        AR’ "'■

Таким же образом определяется и As/AR.

При нулевых начальных условиях: (5ф* )_o. = O - для старта решения при переходе a_o^ а₁ необходимо использовать выражения для толщины потери импульса на плоской пластине [5]:

(5ф*)_1o_ O,O36Лфoo

(5ф*)11 _ O,O36Лфo1

Это допущение вполне справедливо, поскольку s_oo= O, а шаг интегрирования Aa ^ O. Далее на переходе a1 ^ а₂ используется выражение (1O).

Результаты расчета представлены ниже (рис. 2...4).

Анализ полученных результатов показывает, что толщина потери импульса расслаивается в зависимости от радиуса линии тока. Тангенс угла скоса донной линии тока не зависит от радиуса и достигает величины насыщения £ = 1,511.

Справедливость принятых допущений подтверждается совпадением теоретических расчетов (рис. 4) с данными эксперимента по визуализации донных линий тока (рис. 5).

Рис. 2. Зависимость толщины потери импульса от угла поворота потока на круговом секторе с углом поворота потока 90° при скорости потока 25 м/с

Рис. 3. Зависимость угла скоса донной линии тока от угла поворота потока (условия те же, что и на рис. 2)

Рис. 4. Результаты теоретических исследований данных линий тока

На основании вышеизложенного можно сделать следующие выводы:

– получена форма записи уравнения импульсов и дифференциального соотношения на характеристике, позволяющая вести интегрирование совмещенным разностно-характеристическим методом в естественной системе координат с произвольных начальных координат при течении в круговом секторе;

– расчетная и экспериментальная визуализация донных линий тока показывает, что угол скоса этой линии изменяется от нуля в прямолинейном потоке до предельного значения насыщения при повороте потока на криволинейном участке.

Рис. 5. Экспериментальная визуализация донных линий тока при течении в прямоугольном колене (скорость потока 18 м/с)