Невыход летательного аппарата (ЛА) за пределы поля допуска является одной из важнейших в авиации. Характеристика невыхода навигационного параметра, в данном случае – высоты, за заданные пределы позволяет отслеживать то, что самолёт в следующий момент времени не покинет пределы заданного эшелона, что предотвращает сближение воздушных судов. Эту величину также важно знать пилотам, поскольку, даже при правильном управлении, самолёт может выйти за пределы поля допуска в следствии попадания в нестабильные воздушные массы или из-за самих аэродинамических характеристик воздушного судна.

Процессы оценки достоверности невыхода летательного аппарата за пределы поля допуска используются для: обеспечения безопасности полета ЛА; управления ЛА; проектирования новых, более безопасных ЛА.

В этой статье оценивается достоверность невыхода за пределы поля допуска на определенном интервале времени. Поставленная задача решается априорно на основе спектрально-финитного метода и непрерывного базиса Фурье. Для решения задачи используется разложение Каруне-на-Лоэва, которое предполагает решение сложных интегральных уравнений. После чего производится статистический анализ по выборке в 600 реализаций, который сравнивается с теоретическими данными. Помехи в данной работе не учитываются.

Спектрально-финитный метод уникален тем, что освобождает от необходимости решения интегральных уравнений, то есть позволяет избежать поиска собственных чисел и собственных векторов, а значит дает возможность значительно сократить объём затрачиваемой оперативной памяти, требующийся на решение данной задачи.

Задачами исследования, отраженного в этой статье, являются:

• 1.    Разработка и моделирование алгоритма спектрально-финитного прогнозирования полезного сигнала без помехи с использованием непрерывного базиса Фурье;

• 2.    Исследование алгоритма оценки достоверности недостижения измеряемым

• 3.    Анализ полученных данных.

сигналом и его оценкой заданных пределов эшелона на выбранном интервале времени для класса летательных аппаратов при условии, что процесс может выходить из любой точки начала прогноза, известно его распределение в начале, рассматривается марковский стационарный процесс с гауссовским распределением;

В этой статье будет рассмотрен этап установившегося горизонтального полёта.

Описание математического метода

Классическим решением подобных задач является решение на основе уравнения Фоккера-Планка-Колмогорова [1]. Такой подход является очень сложным и ставит большое количество ограничений: необходимость выделить регулярные участки для граничных областей; граничные условия не должны зависеть от времени; решения возможны только в частных случаях при порядке марковских случайных процессов не более второго, но и тогда, в результате решения, получается ряд с низкой сходимостью. С помощью этого метода решается точная задача, но стоит рассмотреть эту же задачу в интервальном представлении: проверить вероятность невыхода за пределы поля допуска на интервале времени.

Предложенный в этой статье математический метод базируется на решении Л. Френкс и В.С. Пугачевым [2] важнейшего случая случайного стационарного марковского процесса с корреляционной функцией:

k ( т ) = а ² e ^{-а ( т} ) . (1)

Моделирование основывается на использовании непрерывного базиса Фурье, для которого справедливо выражение:

T

J K x ( Л , т )у_к Т = a k ^ k ( Л ) , где 0 <  Л <  T .                           (2)

Данное уравнение решено для корреля- случайного процесса по времени пред- ставляет собой представление в евклидовом пространстве, где осями координат выступают значение процесса и время. После разложения в ряд Фурье осуществляется переход в гильбертово, бесконечномерное, пространство, где количество собственных функций определяет размерность пространства.

SL i tVW) (3)

ординат выступают собственные функции и значение в каждой собственной функции.

x(t — T^W^dT (4)

Разложение Карунена-Лоэва обладает следующими достоинствами: ряд Каруне-на-Лоэва обеспечивает наилучшую сходимость среди всех рядов Фурье в среднеквадратическом к представляемому слу-

ционной функции стационарного случайного процесса, найдено бесконечное количество собственных чисел и собственных векторов, что и позволяет сэкономить время и ресурсы на вычисления.

Представленный математический метод позволяет перевести из временного представления непрерывного случайного процесса – в спектральное. Представление

То есть задача решается не в пространстве с координатами время-значение, а в многомерном пространстве, где осями ко- с(() = £

Это позволяет заменить задачу невыхода случайного процесса за пределы поля допуска – задачей невыхода случайных величин, коэффициентов, за пределы, указанные для каждой из них.

чайному процессу; коэффициенты ряда Карунена-Лоэва некоррелированы и при нормальном законе распределения исследуемого процесса независимы; численный метод на основе представления случайного процесса рядом Карунена-Лоэва является более простым методом и применяется для более широкого класса задач.

Преимущества представленного метода:

• 1.    Осуществляется переход случайного процесса к квазидетерменированному;

• 2.    Компоненты охватывают весь рассматриваемый интервал времени;

• 3.    Первая спектральная компонента даёт 98% энергии, поскольку используется разложение Карунена-Лоэва и интервал не длинный (произведение α × t значительно меньше интервала корреляции, что позво-

• ляет не учитывать остальные или учитывать только первые две спектральные компоненты);

• 4.    Обладает высокой универсальностью

• 5.    Не требует марковости и стационарности процесса, единственным ограничением выступает гауссовость рассматриваемого процесса.

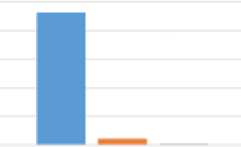
Наибольший интерес у нас будет вызывать первый спектральный коэффициент, поскольку в связи с разложением Каруне-на-Лоэва далее будет происходить сжатие информации и каждый следующий коэффициент будет намного меньше предыдущих, а значит и влияние компонент значительно снизится. Это наглядно иллюстрирует диаграмма (рис. 1).

Алиями* чисел

■ Комлоиеит* 1 ■ Комломемс* 2 ■ Иомлоилны 3

Рис. 1. Влияние первых трех компонент при α=0,01 (Λ1=23,045, Λ2=1,146, Λ3=0,308)

Сравнение статистической и теоретической достоверностей

Статистические данные получены на основании моделирования стационарного случайного процесса с заданными пара- метрами и подсчетом количества выходов за пределы поля допуска с усреднением по количеству реализаций. Получены следующие результаты (рис. 2).

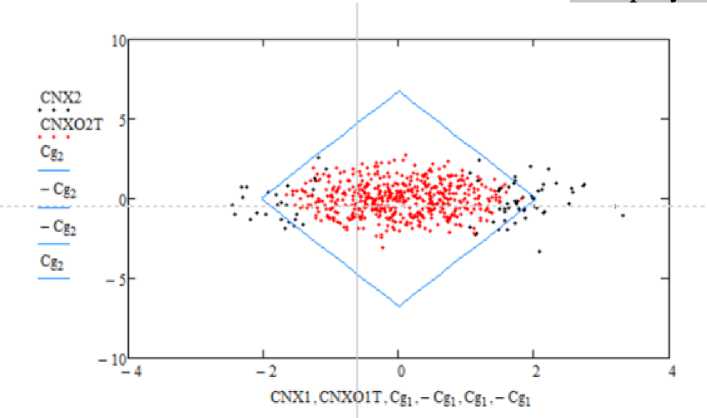
Рис. 2. Проверка поля допуска для компонент

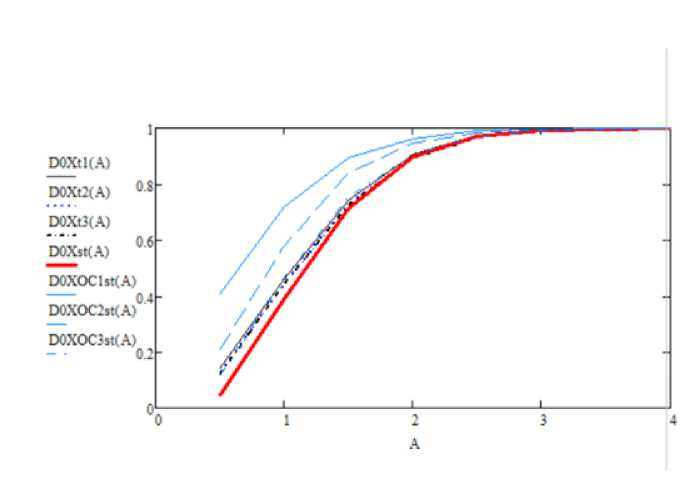
Рис. 3. График зависимости статистической и теоретической достоверности от количества используемых компонент при α=0,01

D0Xt3(A)-D0Xst(A)

D0Xt2(A)-D0Xjt(A)

DOXtKA)-DOXst(A)

DOXOC3st(A)-DOXst(A)

DOXOC2st(A)-DOXst(A)

DOXOC1 st( A)-DOXst( A)

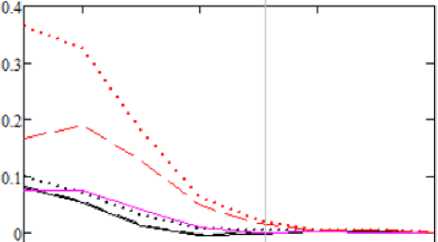
Рис. 4. График зависимости ошибок статистической и теоретической достоверности от количества используемых компонент при α=0,01

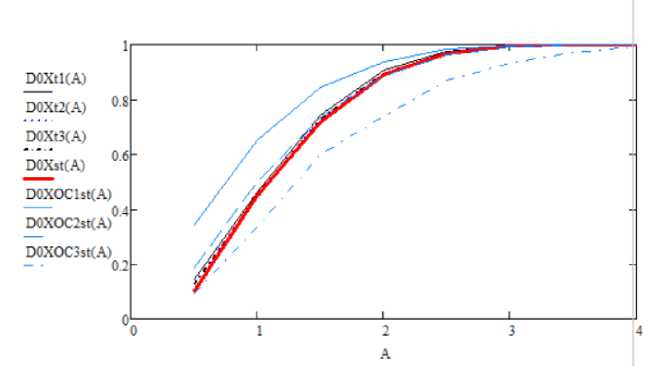
Рис. 5. График зависимости ошибок статистической и теоретической достоверности от количества используемых компонент при α=0,1, тогда Λ1 =2,305; Λ2 =0,115; Λ3 =0,038

D0Xt3(A)-D0Xst(A)

DOXtKA)-DOXst(A)

DOXtKA)-DOXst(A)

DOXOC3st(A)-DOXst(A)

DOXOC2st(A)-DOXst(A)

DOXOClst(A)-DOXst(A)

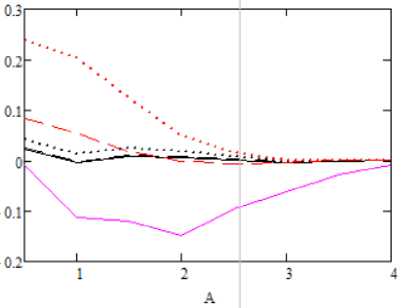
Рис. 6. График зависимости ошибок статистической и теоретической достоверности от количества используемых компонент при α=0,1

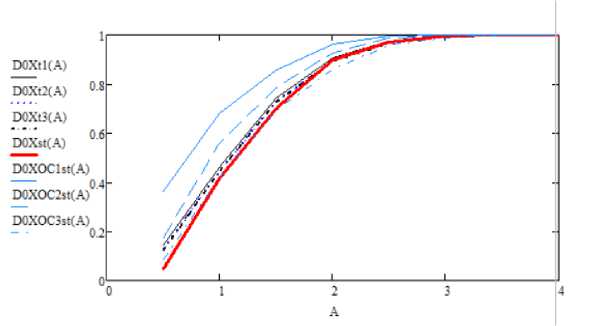
Рис. 7. График зависимости статистической и теоретической достоверности от количества используемых компонент при α=0,05 Тогда Λ1 =4,609; Λ2 =0,229; Λ3 =0,062

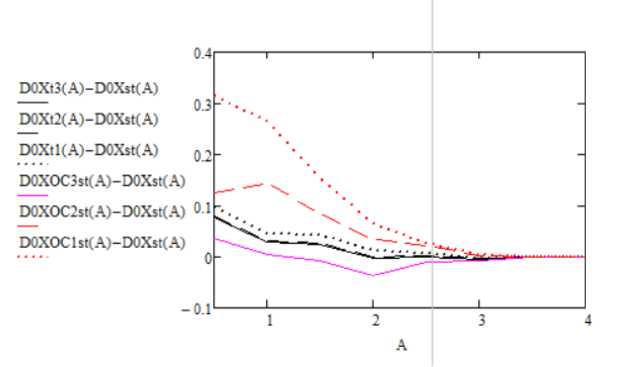
Рис. 8. График зависимости ошибок статистической и теоретической достоверности от количества используемых компонент при α=0,05

На данных графиках видно, что при использовании от одной до трех компонент априорная достоверность по непрерывному базису составляет 95,4-99,7%.

Важно заметить, что представленный метод может быть использован не только в авиационных целях, но и в медицине, например, для прогнозирования состояний пациентов, или на атомных электростан- циях – для отслеживания уровня радиации. Так же в виду своей универсальности он подходит для решения задач с другой заданной корреляционной функцией.

Заключение

• 1.    В этой работе был проанализирован алгоритм спектрально-финитного прогнозирования полезного сигнала без помехи с использованием непрерывного базиса Фурье.

• 2.    Анализ полученных данных показывает, что априорная достоверность по непрерывному базису составляет 95,4-99,7% при использовании от одной до трёх компонент.

• 3.    Данный метод также можно использовать не только для корреляционной функции, представляющей собой экспоненту, но и любой другой корреляционной функции.

  Библиографический список

  
  

  • 1.    Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем: Учебное пособие для вузов. – М.: Радио и связь, 2004. – 608 с.

  • 2.    Пугачев В. С. Теория случайных функций и ее применение к задачам автоматического уравнения: монография. – Москва: Государственное издательство физикоматематической литературы, 1962.

  • 3.    Иванов Ю.П., Бирюков Б.Л. Информационно-статистическая теория измерений. Модели сигналов и анализ точности систем: учебное пособие. – СПб.: ГУАП, 2008. – 160 с.

  • 4.    Иванов Ю.П., Никитин В.Г. Информационно-статистическая теория измерений. Методы оптимального синтеза информационно-измерительных систем, критерии оптимизации и свойства оценок: учебное пособие. – СПб.: ГУАП, 2011. – 104 с.

  • 5.    Пономаренко А.А. Исследование спектрально-финитного метода оценки достоверности безопасности полёта летательного аппарата: бакалаврская работа. – СПб.: ГУАП, 2022. – 50 с.