Исследование движения клубня картофеля на противоточной сепарирующей горке

Клубень на горке вначале скользит и катится одновременно (скольжение с качением), а потом катится по горке без скольжения, при этом он может перемещаться по горке перекатываясь, причем вращение клубня может быть неравномерным. Таким образом, движение клубней на горке значительно сложнее для аналитического описания, чем движение сорняков. На рис.1 показаны два участка на горке: участок 1-2 — скольжение клубня при одновременном качении (качение со скольжением) и участок 2-3 — чистое качение клубня. Для аналитического описания движения клубня на горке примем следующие обозначения: m — масса клубня; г— радиус клубня; Q = m g — вес клубня; N—нормальная реакция горки на клубень; F—сила трения, действующая на клубень от горки; α—угол наклона горки; Vтр — скорость 2             2

полотна горки; Момент инерции клубня, принятого за шар J = m--r2, кгм ; dω е - угловое ускорение вращения клубня, е = —, c ;- а - угловая скорость dt клубня;      t - время; Мт - момент сопротивления качению клубня; M = N ⋅к, hm; К - коэффициент сопротивления качению клубня; K =r⋅tgp , м; где ρ - угол качения клубней; f -коэффициент трения скольжения клубня по горке; as -ускорение центра масс клубня; -скорость клубня вдоль горки; ∆ас - ускорение скольжения клубня, м/с2; as = a =∆a - r ⋅ε-полное ускорение центра масс клубня при скольжении с качением на участке 1-2; (см. рис.1); VH - начальная скорость клубня; V - скорость клубня. В соответствии с принятыми обозначениями движение клубня на горке описывается следующими уравнениями:

m ⋅ a = - Q ⋅ sin α + F (1)

N = Q ⋅ cos α (2)

F ⋅ r = M + J ⋅ ε (3)

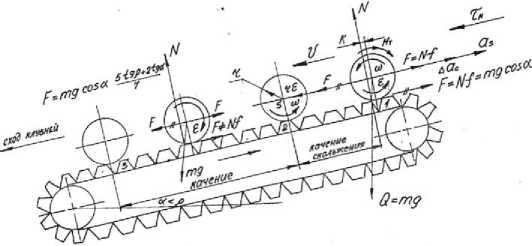
Рис.1 Расчетная схема движения клубня на противоточной сепарирующей горке: 1 - начало качения - скольжения клубня; 2 - конец скольжения, начало чистого качения; 2-3 - чистое качение клубня. На участке 1-2 (см. рис.1) сила трения F

F = N ⋅ f = mg ⋅ cos α ⋅ f (4)

Соответственно уравнение (3) примет вид m ⋅ g ⋅ cosα⋅ f ⋅ r = m ⋅ g ⋅ cosα⋅ r ⋅ tgp + m ⋅ r ⋅ ε откуда:

r ⋅ ε =  - cos α - ( f - tgp )

Уравнение (5) определят ускорение качения клубня на участке 1-2, полное же ускорение на участке 1-as =∆a -r⋅ε, которое определим из уравнения (1),

Подставив в это уравнение значение r - ε из (5), и выразиа ∆а_с, получим

∆ a_s

g ⋅ cos α

dV

(7 f - 5 tgp - 2 tg α ) = ^c dt

где: V c —скорость скольжения клубня на участке 1-2.

Проинтегрировав уравнение (6) получим уравнение:

g ⋅ cos α

V_s =          (7 f - 5 tgp - 2 tg α ) - ⋅ t + c ₁

постоянную интегрирования C I определяем при: t o =0 и V C =-V H

Ci = —V H — начальная скорость подачи клубня на горку в направлении

поверхности горки

g - cos α

V_c =          (7 f - 5 tgp - 2 tg α ) = t - V_H

В точке 2 (рис 1.) скорость V c

0, соответственно время

скольжения t ₂ определяется:

т =

T 2 =

2 V H

g ⋅ cos α (7 f - 5 tgp - 2 tg α

С учетом скорости горки V тр время скольжения t ¹ равно

t 2 ¹

2( V H - V TP )

g ⋅ cos α (7 f - 5 tgp - 2 tg α

Полное ускорение клубня as на участке 1-2 равно as = s • r — Aac = g • cos a( f — tga)    (11)

Скорость клубня V на участке 1-2 получим интегрированием уравнения (9):

V = g • cos a ( f — tg a ) • t + C 1   (12)

При начальных условиях: t0=0 и Vo=-VH, C1=-VH соответственно уравнение

(12) примет вид

V — 2 = g • ^{COS a ( f} - tg ^{a )}t ^— V H

Путь S1-2 определим интегрированием уравнения

S 1 — 2

g • cos ^{a ( f —} tg ^{a )} • t ^V h

• t + C₂

при начальных условиях. t0=0 и S1-2=0, C2=0.

Время t в уравнении (13), соответствующее точке 2, определяется уравнением (9), соответственно подставив в уравнение (13), значение из уравнения (9) получим:

_{s =}   2V ² H(5tgp — tga — 6 f )

2    g • cos 2

Это уравнение (14) не учитывает движение полотна горки со скоростью V Tp . С учетом этой скорости время скольжения t ¹ на участке 1-2 определяется уравнением (10) (см. выше). Тогда путь S_1-2 клубня определится следующим

уравнением:

S 1 — 2

t ¹

g • tg a • ( f — tg a ) -^ — V H

• t 1 (15)

Скорость центра клубня V2 в точке 2 равна.

V 2 = V H ^— g • ^{COS a (}.^{f —} tg ^{a )} • t 2   ⁽16)

Соответсвенно время t з движения клубня по горке от точки 2 до точки 3 равно.

1 3 =     V 2

⁽ r • ^S ) 2 — 3

VH

— g • cos a ( f — tg a ) • t ¹

• g • cos a (tgp — tg a )

Путь клубня S 2-3 (от точки 2 до точки 3) определится

5 2 ⋅ g ⋅ cos α ( tgp - tg α ) ⋅ t ²

_{S 2-3 =} ( r ⋅ ε ) 2-3 ₌ 7                          3   ₍₁₈₎

Общий путь скольжения и чистого качения клубня по горке

S = S 1 - 2 + S 2 - 3 (19)

В точке 3 клубень будет вращаться за счет энергии полотна горки.

Следует заметить, что на участке 2-3 движение клубня описывается уравнениями (1); (2) и (3) в зависимости от величины угла а, т. е. α <р, то будет замедление качения клубня и уравнения будут:

m ⋅ ( r ⋅ ε ) sin α + F (20)

F ⋅ r = M + J ⋅ ε    (21)

Причем F ₃ ^ N • f ; F ₃ = mg - cos a - —(5tgp + 2tga) ^ F

В этом случае из (17) имеем F = m ⋅ r ⋅ ε + m ⋅ g ⋅ sin α ; подставив это значение F в (18) получаем значение замедления качения клубня   ( r ⋅ ε )   при

α<р

( r ⋅ ε )_{2 - 3} =  ⋅ cos α ( tgp - tg α )     (22)

С учетом движения полотна система становится неголономной и ее исследования необходимо проводить энергетическим методом.