Исследование двумерной плазмы на примере полевого транзистора

В последнее время отмечается большой интерес к детектированию терагерцевого излучения полупроводниковыми приборами, связанный с использованием плазменных эффектов. Резонансное и нерезонансное детектирование в таких полупроводниковых приборах, как полевые транзисторы, исследовалось в работах [1–3]. Целью работ [1–3] является создание управляемых напряжением быстрых детекторов терагерцевого излучения. Терагерцовому диапазону (0 , 3–10 ТГц) соответствуют частоты многих возбуждений в конденсированных средах, таких, как фононы, переходы с участием мелких примесей, циклотронный и парамагнитный резонансы, вращательные и колебательные возбуждения в жидкостях, а также газах и биологических объектах. Значительный интерес представляет использование терагерцево-го излучения для неразрушающего контроля и визуализации в медицине, мониторинге окружающей среды, пищевой индустрии, борьбе с терроризмом. В настоящее время для детектирования терагерцевого излучения в основном применяются широкополосные приёмники излучения. Использование селективных и перестраиваемых детекторов при спектральном анализе позволяет отказаться от дифракционных решёток или механически перестраиваемых интерферометров. Во многих случаях предпочтительнее иметь приёмник терагерцевого излучения, перестраиваемый приложенным напряжением. Таким приёмником может быть полевой транзистор с двумерным электронным газом в канале. Поэтому важной задачей является рассмотрение собственных колебаний двумерного электронного газа в такого рода приборах, частоты которых соответствуют тера-герцевому диапазону.

Полевые транзисторы — это полупроводниковые приборы, в которых ток изменяется в результате действия перпендикулярного току электри- ческого поля, создаваемого входным сигналом [4]. Различают полевые транзисторы с управлением посредством изолированного электрода — затвора — это полупроводниковые приборы, в которых ток через канал управляется электрическим полем, возникающим при приложении напряжения между затвором (3) и истоком (1) (рис. 1). Истоком называют металлический электрод полевого транзистора, через который втекают носители заряда, собираемые при выходе из канала другим металлическим электродом — стоком (2). Канал (4) — область полупроводникового кристалла, в которой поток носителей регулируется изменением её поперечного сечения с помощью управляющего напряжения затвора.

Рис. 1. Принципиальная схема полевого транзистора (1 — исток, 2 — сток, 3 — затвор, 4 — двумерный электронный канал)

Исходным полупроводником для полевых транзисторов является AlGaAs, где создан канал из GaAs. Такая структура позволяет удерживать электроны в канале в квантовой яме. При этом канал легируют донорным полупроводником. Тогда при напряжении на затворе относительно истока равным нулю образованный в канале слой квазинейтрален, так как положительный заряд, созданный примесями, имеет ту же плотность, что и плотность электронов. Проводимость канала меняется не за счёт поперечного сечения канала, а

20 Полупроводниковая электроника за счёт изменения концентрации носителей в нём под действием напряжения на затворе. Если характерное расстояние, на котором изменяется потенциал, много больше, чем расстояние между затвором и каналом, мы можем рассматривать канал — затвор — как плоский конденсатор с диэлектриком между ними.

Поверхностная плотность электронов в случае, когда к затвору приложено положительное напряжение относительно канала, имеет следующий вид:

So = ^+ - U ⁰- ,

0 d + 4neW, где Sd — плотность дырок, U0 — потенциал на затворе относительно канала, W — расстояние от затвора до канала. При этом, как показано в работе [5], поведение электронного газа описывается стандартными уравнениями газодинамики в предположении, что имеется возмущение вдоль оси x, а именно уравнением непрерывности:

где G ( £,,£, ' ) — функция Грина.

В силу симметрии задачи распространяющиеся волны могут быть симметричные или антисимметричные. Разлагая выражение (4) в ряд Фурье на отрезке [0 ,а ], получим

V ( х ) = ^ ^=1 2 k - 1 ^cos( п 2 k^-1 х ) для симметричных волн,

V ( х ) = ^ k =1 a k sln( п 2a х ) для антисимметричных волн.

Подставляя эти разложения в выражение (4), получим: ХшSk = 6Sk, Sy

где λ ω

mω ² aκ 2 π ² e ² Σ 0 ,

либо Х _ш a k = 6 kk , S k , ,

6 kk, = ^{п (2 k} - 12⁽² k - 1) | | «с ( и' )

- 1 - 1

/ п (2k — 1)        п (2k' - 1) Д x cos (2---^) cos (-^---^ ) ,   (5)

д S .   .

dt- + div(E v ) = 0

и уравнением движения:

∂v ∂v dt + v^

e E = e_ d£_ m *      m * dx

где S( x,t ) — поверхностная плотность электронов в канале, v = v ( x,t ) — скорость электронов в канале, v ( x,t ) — распределение потенциала в канале, т * — эффективная масса электронов в канале. Также необходимо учитывать уравнение Пуассона, описывающее распределение потенциала в канале и в диэлектрике:

6 kk , =2 пкк ' | I d^d^'G ( ^,^ ) sln( пк^ ) sln( пк ' ^ ' ) .

- 1 - 1

Находя собственные значения бесконечномерной матрицы (5) или (6), из условия Х _ш = А “ или Х _ш = А ® можно найти дискретный спектр частот для волн, распространяющихся в двумерном элек-

д2V , д2 V _ 4пе дх2 + dz2 к (S Sd)5(z), (1) где e — заряд электрона, κ — диэлектрическая проницаемость, 5(z) — дельта-функция Дирака.

Уравнение Пуассона (1) является основным при решении задачи о нахождении спектра собственных колебаний двумерного электронного газа в ограниченном по x и z пространстве. Для решения этой задачи используют формализм функции Грина [6]. Запишем уравнение Пуассона (1) в виде д2V(1) + д2V(1) = —5( )S 4ne2 д2V(1) (2)

∂x2 ∂z2 0 mω2κ ∂x2 , где ϕ(1) — возмущённая часть распределения потенциала. При этом будем учитывать следующие граничные условия:

тронном канале.

Таким образом, решение задачи о нахождении дискретного спектра для волн, распространяющихся в двумерном электронном канале, сводится к решению уравнения (4) с использованием граничных условий (3), следовательно, к построению функции Грина.

Построим функцию Грина при помощи метода электрических изображений. Функция Грина G ( M,M 0 ) для случая двух измерений определяется следующим способом [6]:

• 1)    Д G = 0 всюду в рассматриваемой области S кроме точки M = M 0 ;

• 2)    G \ c = 0, где C — граница области S ;

• 3)    в точке M = M 0 функция G ( M,M ₀ ) имеет особенность вида ¹ Ln ¹   .

2 π   R MM ₀

Здесь M и M 0 — точки в рассматриваемой области, R MM ₀ — расстояние между ними.

Тогда функция Грина имеет вид

G ( M,M 0 ) = ±1п-Д

2 п   R mm 0

+ v ( M,M 0 ) ,

^V l z^ 0 ,z^a    ⁰ .

Уравнение (2) с граничными условиями (3) соответствует краевой задаче Дирихле [6], решение которой имеет вид

V ^{( х} ) ^l z =0 =

4 ne ²

S o mω ² κ

a

[ dXG г ^х.^х ) д , a a ∂x ²

где v ( M,M 0 ) — всюду непрерывная гармоническая функция, удовлетворяющая на границе условию: v ( M,M q ) = 1- In —.

⁰ 2 π R MM ₀

В рассматриваемой нами задаче область S — это бесконечная полоса: х ® у ^ (0 ,а ) • ( —ж , го ).

Пусть точка M 0 ( х 1 ,у 1 ) принадлежит области S (рис. 2). Согласно определению функции Грина, необходимо найти такую функцию v ( х,у ), что 1n | _ж - _у | + v ( х,у ) обращается в ноль на границе

области. Для того чтобы потенциал на границе области обращался в ноль, отобразим ( x 1 ,y 1 ) относительно границ. Получим образы этой точки: ( — x 1 ,y 1 ) и (2 a — x 1 ,y 1 ). Но они создают потенциал на границах x = а и x = 0 соответственно, поэтому отображаем их относительно этих границ и т. д. В итоге для функции Грина получим

_11n x 1 — x 2

2 n   x 1 + x ₂

+ У 1n

2 n

^

П1 — n=1

^

П1 — n=1

G ( x 1 ,y 1 ,x 2 ,y 2 ) =

( x 1 + x 2 ) ² 2   1

4 a ²       n ² n ²

( x 1 — x 2 ) ² 2 1

4 a ²       n ² n ²

1 2 П

^

s .(

V (( x 1 + 2 na ) — x 2 ) ² + ( y 1 — y 2 ) ²

Согласно теореме Римана [7] последнее равенство справедливо лишь при условии сходимости бесконечных произведений. Можно показать, что бесконечные произведения сходятся, причём справедливо следующее соотношение:

— In

V (( — x 1 + 2 na ) — x 2 ) ² + ( y 1 — y 2 ) ²

.

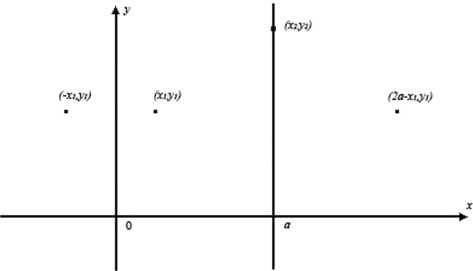
Рис. 2. Иллюстрация к построению функции Грина при помощи метода зеркальных отображений

Положим y 1 = y ₂ в формуле (7), что соответствует переходу к очень тонкому по толщине слою. Рассматривая члены с n >  0 и n <  0, нетрудно преобразовать выражение (7) к виду

G ( x 1 ,y 1 ,x 2 ,y 2 ) = ^У 1n

2 n

x 1 - ξ

x 1 + С

+

+ т E In 2 n ²—^

n = — ^

| x 1 + 2 na — £ | ^

^

+ ^ ^у In

2 n ^

n =1

sin( z )    ^         z ²

= П (1 — nn) ^{, 0} ^ z ^ ^{2 n}'  ⁽⁸⁾

n =1

Применяя выражение (8), получим

G ( x , ,x 2 ) = ± ,„ x 1 — x 2 + ± ,„ ^sin( x ^{1 +} x 2 ) П _

2 n x 1 + x ₂    2 n sin( x 1 — x ₂ ) 2 a

1 , x 1 — x 2      1 , sin( x 1 + x 2 ) n

--1n-------- =  1n 7-------- \ ar •

2 n x 1 + x 2     2 n sin( x 1 — x 2 ) 2 a

Перейдём к безразмерным переменным x 1 = x 1 2 a , x 2 = x ₂ 2 a и окончательно получим следующее выражение для функции Грина:

11 sin( x ! + x 2 )

G ( x 1 ,x 2 ) = —- 1n     ¹----2- , 0 ^ x 1 ± x 2 ^ 2 П.

2 n   sin( x 1 — x ₂ )

Рассмотрим ещё один подход к построению функции Грина, а именно предельный переход от прямоугольника к бесконечной полосе. Как известно, для простейших областей (круг, прямоугольник и др.) решение краевых задач можно получить методом разделения переменных [6]. Покажем, что исходную краевую задачу можно решить следующим образом.

• 1)    Решение задачи для прямоугольника (рис. 3).

• 2)    Сведение полученного решения к решению для бесконечной полосы с помощью метода предельного перехода от прямоугольника к бесконечной полосе.

-

2 п

oo

— - ^у In

2 n ^

n =1

= ^1n

2 n

| x 1 + 2 na — £ |

— 1

у 1n

n = — ^

-

|— x 1 + 2 na — £ |

|— x 1 + 2 na — x ₂ |

1   ^

+— у In

2 n n=1

o o

— Л ^у In

2 n ^

n =1

x 1

-

x 2

x 1 + x 2

-

( x 1 — ^ ) ²

= — In 2 n

— 4 n ² a ²

( x 1 + x 2 ) ²

+ 1П

2 n

^

П n =1

^

П n =1

x 1

-

—+

x 1 + x 2

-

— 4 n ² a ²

( x 1 — x 2 ) ²

— 4 n ² a ²

Рис. 3. Иллюстрация к построению функции Грина при помощи предельного перехода от прямоугольника к бесконечной полосе

( x 1 + x 2 ) ²

— 4 n ² a a 2

Рассмотрим следующую задачу: найдём функцию u ( x,y ), удовлетворяющую внутри прямоугольника уравнению Л u ( x,y ) = — Ф( x,y ) и принимающую на границе заданные значения: ^u \ x =0 = / 1 ⁽ У ), u l x = a = f 2 ⁽ У ), ^U \ y =0 = f 3 ^{( x} ), u | y = b = f 4 ( x ). Как известно, решение такой задачи имеет следующий вид [8]:

ab

u

^{( x,}y >=и

Ф( £,’ ) G ( x,y£,n ) dd’ +

ТРУДЫ МФТИ. — 2010. — Том 2, № 1(5) Подставляя выражения (11) и (12) в исходное уравнение, получим

d ² u m dy ²

π_am 2 _{u m}

Ф

m .

Решение этого уравнения можно записать в

b следующем виде [8]: Um(y) = g g„y(y,n) Фm(n)dn, где gm(y,n) = msh(nmb) X

b

⁺ | f 1 ⁽ П ) d j G ⁽ x^^-’ ) \ _{£ =0} dn^—

b

^— j / 2 ⁽ n ) dd G ⁽ xy^n ) \ _£ = a dn ⁺

0 a

⁺ f з ^{( £})4- ^{G ( x,}y^t-n ) \„__od€^— dn             ⁿ =⁰

a

^— j / 4 ^{( £} ) dn G ⁽ xy^n ) \ _n = b ^d^.       ⁽¹⁰⁾

Рассматриваемая задача эквивалентна пяти зада- чам:

• 1)    ^Л u = 0, u \ x =0 = f 1 ⁽ y ), u \ x = a = 0, u \ y =0 = 0, u \ y = ь = 0;

• ^{2) Л} u = 0, u \ x =0 = 0, u \ x = a = f 2 ⁽ y ), u \ y =0 = 0, u \ y = ь = 0;

• 3)    ^Л u = 0, u \ x =0 = 0, u \ x = a = 0, u \ y =0 = f 3 ⁽ x ), u \ y = b = 0;

• ^{4)    Л u} = ⁰, u \ x =0 = ⁰, u |x = a = ⁰, u \ y =0 = ⁰ , u \ y = ь = f 4 ^{( x} );

• 5)    ^Л u = ^— Ф, u \ x =0 = 0, u \ x = a = 0, u \ y =0 = 0, u \ _y = b = 0. Общее решение рассматриваемой задачи есть сумма решений всех 5-ти задач. Решение задач 1–4 получается стандартным методом разделения переменных и имеет, например, для третьей задачи следующий вид:

Г ^sh( nm n ^{)sh n}m ⁽ b ^— y )) , y ^ n ^X t sh( ⁿm y )sh ⁿm ( b — y )) , y X n ⁽¹³⁾

Таким образом, искомая зависимость u _m ( y ) в решении пятой задачи (11) определяется выражением (13). Суммируя решения задач 1–5, можно получить общее решение поставленной задачи. Тогда функция Грина в выражении (10) будет иметь вид

2 ^О

G ^{( x,}y,^,n ) = - 52 a

sin( p n x ) sin( p n ^ ) _x P n sh( p _n b )

( sh( p n y ) sh( p n ( b — n )) , b ^ n ^ y ^ 0

( sh( p n n ) sh( p n ( b — y )) , b ^ y ^ n ^ 0

где p n =

πn

. a

Симметризуем прямоугольник относительно y = 0 преобразованием y ' = y + b и n ' = n + 2 . Получим

ГГт » f - ² V ^sin( p n x ) ^sin( p n ^ ) V

^{G (} x^-’¹ ) = a 4   p n sh( p n b )    ^X

_X Г sh⁽ p n ⁽ y ⁺ 2 ^))sh( p n ⁽ 2 ^— n )) , b >  n >  y >  ^— b , ( sh( p n ( n + b )) sh( p n ( 2 — y )) , b ^ y ^ n ^ — b .

Устремим b ^ ж и положим y = n , что соответствует переходу к бесконечно тонкой полосе. В результате для функции Грина получим

О

G ⁽ xt ) = a E n =1

sin( p n x ) sin( p n t ) ^{2 p} n

^{u ( Х,}У ) =

^f /2 ^V sh ^ПП ( b — y ) a ^  sh ⁿn b

sin( —x ) sin(— aa

^{ 0

dξ.

О

= V n=1

cos( x — t ) ⁿn — cos( x + t ) nn

2 nn

Получим решение пятой задачи. Поскольку функция sin( ⁿm x ) удовлетворяет граничным условиям рассматриваемой задачи: sin( ⁿm x )| x =0 = sin( nm x )| x = a = 0, будем искать решение в виде

X_ln ^sin( 2 a ^{( x +} ^ )) ^{2 n    sin(} 2 a ^{( x —} £ ))

u ( x,y )

= ^ U m ( y ) sin (^ - ^x) .

m =1

Разложим Ф( x,y ) в ряд Фурье по x :

О О

Ф( x,y ) = ^ Ф m ( y ) sin (- ^x) .     (12)

^{0 X (} x ± ^£ ) ^{n X 2 n}.

2 a

Полученный результат совпадает с формулой (9). Заметим, что функция (9) разрывна при x '1 = x 2 , что соответствует одному из свойств функции Грина [6]. Покажем, что выражение (20) удовлетворяет также следующему свойству: функция Грина имеет вид 5 -функции при x '1 ^ x 2 ^ 0. Известно [6], что функции Грина для уравнения теплопроводности для отрезка и прямой переходят в функцию 5 ( x — x 0 ) при t ^ 0. Аналогичным образом можно показать, что выражение (9) при

X ₁ ^ x 2 ^ 0 переходит в 5 ( X 2 ). Для этого зафиксируем значение Х ₁ = 0, 001 и построим график зависимости G ( Х ₁ = 0 , 001 ,Х 2 ) (рис. 4). Из графика зависимости, изображённого на рис. 4, следует, что при Х ₁ ^ Х 2 ^ 0 функция Грина G ( Х ₁ ,Х 2 ) переходит в дельта-функцию.

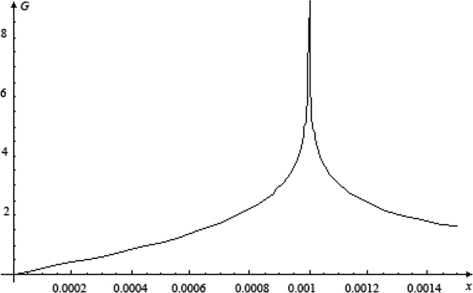
Рис. 4. Зависимость функции Грина от одного из аргументов при фиксированном втором в окрестности нуля

Итак, мы получили решение уравнения Пуассона для распределения потенциала в электронном канале полевого транзистора с заданными граничными условиями. Решение уравнения Пуассона проводилось на основе формализма функции Грина двумя различными методами: методом электрических изображений и методом предельного перехода от прямоугольника к бесконечной полосе. Результаты, полученные первым и вторым способами, совпадают и обладают свойствами функции Грина. Полученные формулы являются основными для расчёта дискретного спектра колебаний двумерного электронного газа, частоты которых лежат в терагерцовом диапазоне.

В статье рассмотрена модельная ситуация, когда частоты столкновений с электронов фононами и примесями являются малыми по сравнению с собственными колебаниями плазмы. В принципе такая ситуация характерна для двумерного электронного газа. Кроме того, использование донорного полупроводника может создать в электронном канале высокую плотность электронов, так что взаимодействие электронов и примесей будет малым.

Учёт диссипативных процессов, а именно столкновение с фононами и примесями, приводит к тому, что существует возможность рассмотрения нелинейных плазменных эффектов [9], кото- рые приводят к генерации плазменных волн тера-герцового диапазона. В работе [9] аналитически и численно показано, что в зависимости от того или иного диссипативного эффекта в двумерном электронном газе возможно возбуждение ударных волн или солитонов с помощью излучения, частоты которых лежат в диапазоне 1011 Гц. Таким образом, за счёт нелинейных эффектов возможно создание генератора терагерцового излучения на основе полевого транзистора.