Исследование ферритового преобразователя температуры системы контроля нагрева технических устройств

тический компенсационный преобразователь амплитуды импульса в постоянное (квазипостоян-ное) напряжение, МИУ – масштабный импульсный усилитель, СС – схема сравнения, ИОН – источник опорного напряжения, БП – блоков памяти, БЛ – блок логики, БСИ1-БСИ3 – блоки световой индикации, БЗИ – блок звуковой индикации, ФНЧ – фильтр нижних частот, БКЗ – блок контроля короткого замыкания датчика на корпус. Временные диаграммы и алгоритм работы данного устройства подробно изложены в [1].

Основой построения подобных систем является её первичный преобразователь (чувствительный элемент), в качестве которого предлагается использовать ферритовое кольцо. Как и у любого преобразователя, для использования его в данных целях необходимо знать его выходную статическую характеристику, т.е. зависимость его выходного параметра от входного, которыми, соответственно, являются выходное напряжение и температурное воздействие. Её получение является задачей исследования ферритового преобразователя температуры системы контроля нагрева технических устройств.

Физические явления в чувствительных элементах из ферромагнитных материалов широко освещены в [3, 4]. Намагниченность домена (области самопроизвольного намагничивания) равна намагниченности насыщения материала при данной температуре, поэтому существенно изменить намагниченность домена можно только путем изменения температуры. Магнитный момент каждого домена определяется значением и направлением намагниченности домена и его объемом. Однако при наложении внешнего магнитного поля изменяется свободная энергия домена за счет появления энергии магнитных моментов во внешнем поле. В результате домены приобретают новое равновесное состояние.

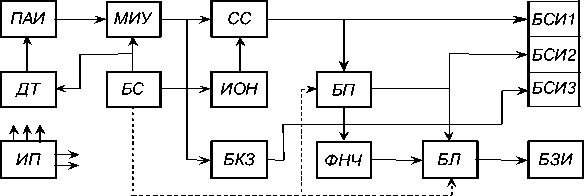
Рис. 1. Структурная схема системы контроля температуры нагрева

Намагниченность J ферромагнитного образца при постоянной температуре и намагниченности J_s домена изменяется за счет следующих процессов: 1) перемещения границ и соответствующего изменения объема доменов при росте тех из них, у которых J_s составляет острый угол с Н ; 2) вращения, связанного с поворотом вектора J_s внутри доменов. Оба процесса разделяются на обратимые и необратимые [5].

В общем виде точное аналитическое описание процессов, происходящих в ферромагнитном материале под действием низких температур (температур ниже точки Кюри) достаточно сложно и мало пригодно для выполнения инженерных расчётов. Предлагается температурные напряжения в ферромагнитном образце рассматривать как механические, влияние которых на намагниченность известно [4].

При нагреве ферритового кольца в нем возникают механические напряжения

σ_{Δ T} =σ ( Δ T ) = E αΔ T , (1) где E – модуль Юнга ферритового материала, α – температурный коэффициент линейного расширения, Δ T – изменение температуры, относительно 20 °С ( Δ T = T - 20 ° C ).

Плотность свободной энергии ферромагнетика включает в себя следующие основные составляющие: плотность обменной энергии, плотность энергии анизотропии, магнитоупругой и собственной магнитной энергии доменов, энергии внешнего магнитного поля [8]:

W = W + W + W + W + W об ан σ _{Δ T} м н .

Рассматривая различные случаи взаимного расположения векторов напряженности магнитного поля и вектора механических напряжений, вызванных изменением температуры, можно принять что изменение свободной энергии в основном равно W = W _{σΔ T} + W_н . Остальными видами энергий можно пренебречь.

Используя выражения для магнитоупругой энергии и энергии внешнего магнитного поля, запишем выражение плотности свободной энергии ферромагнетика

W = ₂ λ _s σ_{Δ T} sin² η- J _sH cos( θ ₀ -η ) , (2) где λ _s – изотропная магнитострикция, η – угол между векторами J_s и σ , θ ₀ – угол между век-

торами H и σ [5]. Исходя из условия минимума плотности свободной энергии продифференцируем (2) и найдём

H _=- 3 λ _s σ_{Δ T} sin2 η 2 J _s sin( θ ₀ -η ) ^.

Из термодинамических соотношений для обратимых термомагнито-механических процессов [4] следует, что H = H ₀ - H _{σΔ T} , где H ₀ , H _{σΔ T} – соответственно напряженности магнитного поля, необходимые для достижения необходимого значения намагниченности J при σ_{Δ T} = 0 и σ_{Δ T} ≠ 0 . Считая, что магнитная проницаемость ферромагнетика больше единицы можно записать выражение, связывающее изменение магнитной проницаемости ферромагнетика любой конфигурации в направлении действия магнитного поля с действием нормальных термомеханических напряжений (1)

3 λ              sin 2 η

Δ µ =-    ^s σ Δ T µ н µ σ

4 π J ² _s           ^{Δ T} sin 2( θ ₀ - η ) ^{. ()}

Учитывая, что под действием температуры в кольце механическое напряжение возникает в основном в радиальном направлении, то можно получить следующее выражение взаимосвязи изменения температуры и магнитной проницаемости ферромагнетика

Δµ = 0,375

λ _s α _s µ ² _нE αΔ T π B ²

Тогда, магнитная проницаемость (абсолютная) чувствительного элемента при различных температурных воздействиях определяется выражением

µ σΔT = µ н

-

_{0 375} λ s α s µ ² н E αΔ T

^,           π B ²

.

Формула (6) даёт достаточно точные результаты и легко может быть применена для инженерных расчётов. На рис. 2 приведены графики зависимости относительной магнитной проницаемости от температуры. Сплошной линией показана теоретическая зависимость µ ( Δ T ) для материала 1000НН, рассчитанная по (6), точками – экспериментальная зависимость для того же материала [6].

Для получения выходной статической характеристики вначале необходимо определить электрические параметры (сопротивления) чувствительного элемента. Определение последних сводится к задаче с сосредоточенными параметрами, т.е. к задаче электрических цепей, что достигается введением в расчет эквивалентных глубин проникновения электромагнитного поля в материал кольцевого элемента [7].

Для упрощения анализа электромагнитных явлений кольцевой элемент заменяется эквивалентной пластиной в электромагнитном поле (рис. 3). При этом принимается ряд следующих допущений:

• 1)    магнитная индукция внешнего электромагнитного поля, в котором находится пластина, изменяется по синусоидальному закону;

• 2)    магнитное поле равномерно и имеет только нормальную составляющую магнитной индукции B _z ;

• 3)    комплексная магнитная проницаемость ^Ц пластины зависит от значения температуры D T , Ц = f ( T ) ;

О д T ⁷

• 4)    плотность токов 5 _х , 5 у по толщине с пластины не изменяется, что имеет место при c /(2 А ) <  0,5 , где А - эквивалентная глубина проникновения электромагнитного поля в пластину;

• 5)    тангенциальные составляющие напряженностей электрического поля E _a и E _b на гранях пластины постоянны;

• 6)    поля выпучивания, идущие в обход пластины, относятся к полям рассеяния;

• 7)    среда пластины анизотропна или изотропна.

При принятых допущениях состояние ферромагнитной пластины (кольца) при температурном воздействии для двумерного пространства в декартовых координатах описывается системой дифференциальных уравнений электромагнитного поля, ферромагнетизма и термоупругости [10]:

д H z

д у

= у Е • I X —X ;

д H z

= у Е • ' у —у ;

^^^^^^е д х

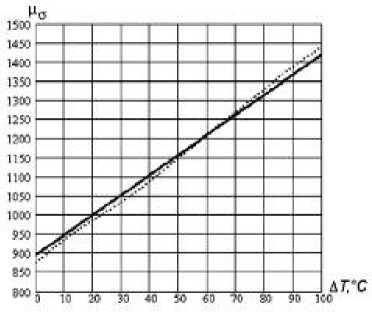
Рис. 2. Графики зависимости относительной магнитной проницаемости от температуры

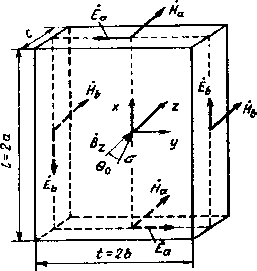
Рис. 3. Распределение электрического и магнитного полей в чувствительном элементе

• д Еу д Ex.

  ---= j ®Ц

• д х    д у         Од T    ;(9)

дBz _ 1 дBz дHz д оАт_ дHz J2 дHz д оАт дАT °Ат ”-°дт ’ (10) где Yх, Yу — удельные электрические проводимости по направлениям х и у; Ех, Еу, Hz -комплексы действующих значений напряженностей электрического и магнитного полей на поверхности пластины по осям х, у, z; ю - круговая частота.

Граничные условия при этом имеют вид (рис. 3):

	H z ( у ) при	x _ ± a ;
H z ( X , у ) _•	H a    при 0      при	x _ ± а; у _ 0 у _ ± ь ;

	" H z	( х ) при	у _	± ь ;
H z ( у , х ) = •	H b	при	У _	± Ь; х = 0
	. 0	при	х =	± а ;

О а t|_s _А T S ;0 <в о <п /2 , (11) где О д т - механические напряжения в пластине, вызванные изменением температуры А T [5].

Уравнение (10) в системе уравнений (7) – (10) было решено выше и его решением является зависимость магнитной проницаемости от изменения температуры (6).

Совместное решение (7) – (9) дает д2 h д2 h

H z = 2, 2 ⁺ 2. 2 = H z ^{( х} , у ) ⁺ H z ⁽ у , ^х ) ,(12)

X х д х X у д у где

Г--------------_ e1

X х = Vj Ю Y у Ц °АГ = Д ’ А х = / А X         >Y у Цодт ej

Xу Vj YхЦодт    д ; у     ,ю у              Xj ‘ X G А т

X _х , X _у - постоянные распространения электромагнитной волны в материале пластины;

A x , A y – эквивалентная глубина проникновения электромагнитного поля в материал; V = n /4 — P /2 - фазовый угол между индуктированной ЭДС и вихревым током; в - угол магнитных потерь.

Поскольку постоянные (13) есть величины комплексные, то решение уравнения (12) ищется в комплексном виде через круговые и гиперболические функции

H z ^{( x} , y ) = A ^ch X x ^cos qy ;

H z ( y , x ) = B ch X y cos px .     (14)

Из условия (11) определяются постоянные A и B, которые подставляются в (14), преобразуя его к виду

H z ^{( x} , y ) = H a ^h ^ ^ ^ cos qy ;

^ch X x a

5 y

^d H z ^{( x} , y ) __y E shX x^x

5 x       ^y~^a sh X _xa

где

E a ^{_ —} P y X x^Ha ^th X x a ^{_ —} j ^Ю B a a B ;

E b ^_— P x X y^Hb ^th X y b ^_— j ю B b b B ; (21)

4 ^ro ф n ^{( x} ) ^_- E

^П n " 1

Ф n ⁽ y ) ^_-

П

1 . П n    n nx

—sin — cos--- n 2     2 a

ro z n _ 1

1 . n n    n ny

—sin — cos--- n 2     2 b

ch X y

H z ⁽ y , ^x ) ^{_ H}b ——- ^cos P ^{x ch} X y^b

.

Третьи условия из (11) удовлетворяются при qb = pa _ n n /2 , тогда

ГО

H z ⁽ a , y ) ^_ E b n n _ 1

n n cos     y ;

2 b

где

ro

Hz (b, x) _S an i _1

n n cos x

2 a '

^ + a an_ v jHz(b,x)

2 a

— a

n nx cos--- _

2 a

4 Hb nn

• n n sin —. 2 ^;

1 +b’ bn _   № (a, y)

2 b

— b

^П ny _ ⁴ H a

cos—— =

2 b    n n

• n n sin

– коэффициенты Фурье ( n = 1,3,5...[5]).

Из (14) – (17) окончательно находим

H z ( x , y ) _ H a 'h ^X "  ф n ( y );

ch X _x a

B a , B b – комплексы действующих индукций, равномерно распределенных на эквивалентных глубинах a_B и b_B , которые позволяют найти участки l_э и t_э эквивалентного контура L_э вихревых токов [5].

В эквивалентном контуре действует ЭДС

Э _ 2( E a t э + E b l э ) _— j ю Ф .     (23)

Единичные функции (22), представляющие граничные условия, существенного влияния на результаты анализа не оказывают и могут быть положены ф _n ( x ) _ ф _n ( y ) _ 1 .

Полученные выражения (20) – (23) с учетом формул расчёта магнитной проницаемости чувствительных элементов при температурном воздействии (6) помогают определить сопротивления чувствительных элементов магнитоанизотропных преобразователей вихревому и намагничивающему токам при действии на них изменения температуры.

Вихревые токи в эквивалентном контуре Ь э _ 2( t э + 1 э ) пластины находятся путем интегрирования выражений (20):

, f o ,    cE_a ch a — 1

I_t B _ c 5 dx _ a

^J _n y PX ^sh X a ^;

I lB

b

^{_ c} j ⁵ x dy

cE_b ch b — 1 PX ^sh X ^b

ch X y

H z ( y , x ) _ H_b-^- Ф n ( x ), ^ch X y^b       ’

Сопротивления пластины вихревым токам вычисляют с учётом выражений (21), (23) и (24):

тогда уравнения (12), (7) и (8) принимают вид соответственно

chx^ x           ^{ch x} y y

H z ^_ H a™ ---Ф n ⁽ y ) + ^Hb "Г--"Ф n ^{( x} )'(19)

^ch X x^{a             ch} x y^{b       ;( 9}

7 Z tB	_ 2 l ItB	_ -t ^ p ej V a ; caE
Z lB	_ Эе I lB	_     p eJ V b cbE       .	(25)

5 x

^d H z ⁽ y , ^x ) 5 y

^— Y x E b

^sh X y y ^sh X y^b

Ф n ^{( x} )

;

Полное сопротивление вихревому току запишем как сумму выражений (25)

Z b _ 2( Z t _B + Z i _B ) _ 2 p

( t

Еэ- e V a ( ^caE

--^-e^{J V} b cb_E

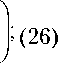
где р - удельное электрическое сопротивление чувствительного элемента (кольца); t_э , l_э – стороны эквивалентного контура вихревых токов; с – средняя длина пути магнитного потока; V a , V ь — углы сдвига между вихревым током и ЭДС по соответствующим направлениям эквивалентного контура.

, a ch k 1 - cos k 2

aE = bE = 7 л --- 7-      (27)

k у ch k 1 + cos k ₂        ^v '

– эквивалентные глубины проникновения электрического поля в пластинунайденные с учетом выражений (13);

k = a / Д = aj oyu^ T ;

k 1 = k cos( n /4 -в /2) ;

k 2 = k sin( n/4-в/2);(27а)

у = 1/ р = у cos ф - j у sin ф .

Углы сдвига между вихревым током и ЭДС k sh k + k sin k cos va = cos vb = —1   1   22

k sh² k 1 + sin² k ₂ ^;

k sh k - k sin k sin v„ = sin v?> = —2    1    12

a kд/sh2 k 1 + sin2 k2

Сопротивления пластины намагничивающему току I ф = cH по соответствующим направлениям эквивалентного контура определяют с учетом выражений (21) и (23):

^ZtФ = Э, ^/( cH t ) = to ^tэ a B М „ _Д T e ^a a / С ;

Z „ = Э , /( cH , ) = ю ^bB u . . T e* “ • I c , (29) а полное сопротивление чувствительного элемента намагничивающему току запишем как сумму выражений (29)

Z Ф = 2( Z ^ + Z_№ ) =

= 2 ^^ ( t_эa B e j ^a + l₃b_Be^{j a} B )     ⁽³⁰⁾

где цОдT - магнитная проницаемость пластины с учетом (6), a a, а в - углы сдвига между намагничивающим током и магнитным потоком по соответствующим направлениям эквивалентного контура;

^а в = ^ь в

a ich2 k 1 - cos 2 k ₂ k у ch 2 k 1 + cos 2 k ₂

– эквивалентные глубины проникновения магнитного поля в пластину, найденные с учетом выражений (13); k , k ₁, k ₂ определяются по (27а);

n   = ц„ cos a- j ц„ sin a

—°_Д T ^^а Д t        ^^а Д t      .

Углы сдвига между намагничивающим током и магнитным потоком k2 sh 2 k, + k, sin 2 k2 cos a a = cos a b = —2    11     2 -.

k \sh^:2 k 1 + sin² 2 k ₂ ^;

sin a _a = sin a _b

k 1 sh2 k 1 - k 2 sin2 k ₂

k a] sh² 2 k j + sin² 2 k ₂ ^{. (32)}

При отсутствии поверхностного эффекта, что имеет место при k = a^гоцадг у < 0,5 , эквивалентные глубины проникновения электрического и магнитного полей будут bB = b, aB = a, bE = aE = 0,5aB , а магнитная индукция распределяется равномерно по сечению Bc = BaB / a [7]. При этом можно пренебречь составляющими, пропорциональными круговым функциям в выражениях (28) и (32). Тогда cos v = sin a = k2 / k = sin(n /4 - в /2);

cos a = sin v = k 1 / k = cos( n /2 - v) . (33)

С учетом изложенного, сопротивление вихревому току элемента любой конфигурации, приведенное к виткам соответствующей обмотки, приобретает вид

Z b ⁼

P L₃ k² n e^j

caE

где L₃ = t + 1 - длина эквивалентного контура вихревых токов; t = 2 b , l = 2 a - ширина и толщина; k n = w / w₄ - коэффициент приведения сопротивления чувствительного элемента к соответствующей обмотке w ; w₄ = 1 - число витков чувствительного элемента.

Активная и индуктивная составляющие сопротивления вихревому току rB = ZB cos v; xB = ZB sin V . (35)

Полное электрическое сопротивление чувствительного элемента любой конфигурации намагничивающему току (30), приведенное к виткам соответствующей обмотки, принимает вид [5]

ю L^a_n             ю s_Q

^ZФ = ^T B П_ПД T ^k„e ^j = -ЭУ Ц_СТД T ^k„e ^j , (36) где 5 э = 5 = L₃ a B = tl при отсутствии поверхностного эффекта.

Активная и индуктивная составляющие ZФ гФ = ZФ sin a; хФ = ZФ cos a.    (37)

Приведенная к первичным виткам ЭДС эквивалентного контура

Э = to B_c5 Э W 1 .

Поскольку сопротивления вихревому и намагничивающему токам расположены относительно друг друга параллельно [7, 10], то комп- лекс полного результирующего сопротивления чувствительного элемента

Z_p = Z b Z Ф /( Z b + Z Ф ) ,        (39)

а активная и реактивная составляющая при этом

Г р = Вф /(г в + Г ф );    X p = Х в Х ф /( X b + Х ф ) . (40)

Сопротивление намагничивающему току Z_Ф изменяется при действии изменения температуры (напряжений с_д т ), и выражение (36) с учетом формулы расчёта магнитной проницаемости чувствительного элемента (6) приобретает соответствующий вид:

ю > Г    ..^./jul E aA T

2 фра. =     1н н - 0 ^!/5     П н;'----- 1 k" e . (41)

Зависимости (34) – (41) позволяют определить электрические сопротивления чувствительных элементов магнитоанизотропных преобразователей и, соответственно, электрические потери и тангенс угла магнитных потерь tg b при температурном воздействии на них.

Магнитная цепь дифференциально-трансформаторного магнито-анизотропного преобразователя имеет схему замещения, приведенную на рис. 4.

Для этой схемы по второму закону Кирхгофа составляем систему уравнений [7]:

U ч + U к = U 1 ;

U ч - U к - U с = о ,      (42)

где U_ч , U к , U с — соответствующие напряжения на чувствительном и компенсационном элементах и контурном конденсаторе С ; U 1 - напряжение питания преобразователя.

После перехода к магнитным индукциям система уравнений (42) принимает вид вч + в к = в 1; вч - в к - в С = 0,  (43)

где Bч, Bк - магнитные индукции в сердечниках чувствительного и компенсационного элементов; Bi, Be — магнитные индукции в сердечниках элементов за счет напряжения питания Ui и на конденсаторе соответственно, вч = (H1 + H 2) м„, в к = (H1 - H 2) мк, чк

B 1 = U 1 /( ю sw 1 ) , в_С = H ₂ С /( ю ² sw ₂ ² C ) . (44) Здесь H 1 , H 2 - напряженности магнитного поля, создаваемые в сердечниках чувствительного и компенсационного элементов за счет протекания тока в первичной и вторичной (измерительной) цепи преобразователя [5];

^М _ч = М ч ^- j М ч tg P ч ,

^М к = ^Ц к ^{- j Ц} к ^tg P к ,         ⁽⁴⁵⁾

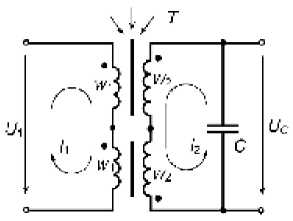
Рис. 4. Магнитная цепь дифференциальнотрансформаторного магнитоанизотропного преобразователя

М _ч и М _к - комплексные магнитные проницаемости чувствительного и компенсационного элементов; tg в _ч и tg в к - тангенсы магнитных потерь чувствительного и компенсационного элементов, ю - круговая частота питающего напряжения; s – сечение магнитопроводов коль-цевыхэлементов; W 1 и w 2 - число витков обмоток возбуждения и измерительной; с - средняя длина пути магнитного потока в элементе.

Подставив (44) в (43), получим

H 1 ⁽ М„ + М, ) + H 2 ⁽ М„ -М, ) = ^U 1 ^{/( ю sw} 1 ) ; чк   чк

H 1 ( М ч -М к ) + H ₂[ М _ч +М к - c /( ю ² sw ² C )] = 0. (46)

Решив данную систему методом определителей, имеем

U 1 ( М _к -М _ч ) ю Ck T w ₂

H 2

c ( м +М ) - 4 м М ю ² Csw ² , ⁽⁴⁷⁾ —ч —к    — ч— к       ²

где М _к - М _ч = ^М - изменение магнитной проницаемости под воздействием температуры (6); к т = w 2 / W 1 - коэффициент трансформации чувствительного элемента; W 1 = U 1 /8,88 f Btl -число витков обмотки возбуждения; f – частота питающего напряжения, s = tl – сечение элемента;

² x р ^-^ х р ю (2Z р -Д 2_р )²

– ёмкость контурного конденсатора, определяемая из условия резонанса токов при максимальной температуре; A x р , A Z p - изменения индуктивного x_p и полного Z_p сопротивлений чувствительного элемента при воздействии на него, определенные по выражениям (39), (40), приведенные к той обмотке, в которой включен контурный конденсатор С .

После подстановки в (47) значений вышеназванных величин и выражений (6) действующие значения напряженности магнитного поля Н ₂ после соответствующих преобразований принимает вид [5]

H ₌ U ₁ k_T λ _s α _s µ _н fw ₂ CE αΔ T

² 3,353 π B ² ( r ₀ - 4 πµ _нf ² Ctlw ₂²) ^{. (49)}

Выходное действующее напряжение U ₂ , снимаемое с конденсатора С, записывается выражением

1     H ₂ c 1       r ₀

U 2 ⁼ I 2      ^{=         =}      H 2 , (50)

ωC w ωC fw C , или после подстановки (49) в (50)

U ₌     U ₁ k_Tr ₀ λ _s α _s µ _н E αΔ T

² 3,353 π B ² ( r ₀ - 4 πµ _нf ² Ctlw ₂²) ^{. (51)}

Таким образом получено выражение выходной статической характеристики U ₂ = f ( Δ T ) магнитоанизотропного преобразователя температуры на кольцевых ферритовых чувствительных элементах (рис. 5). Расчёты данной характеристики имеют погрешность не превышающей 5%, что подтверждено экспериментально.

Данный преобразователь может быть использован в различных устройствах контроля нагрева и автоматики, где осуществляется измерение температуры, например, в бортовых системах контроля нагрева букс осей железнодорожных вагонов.