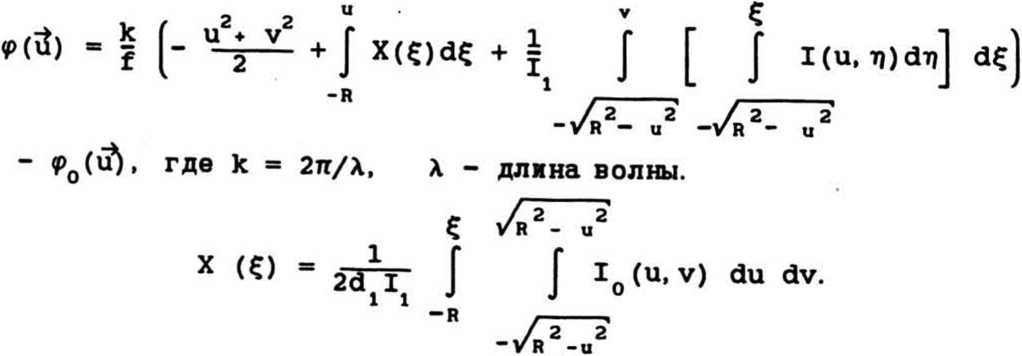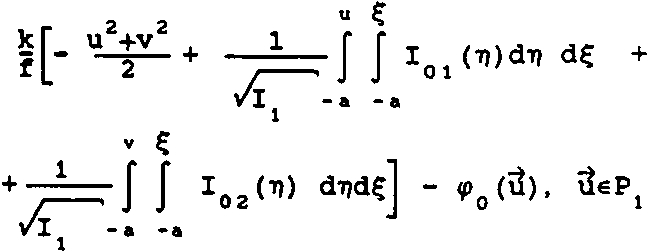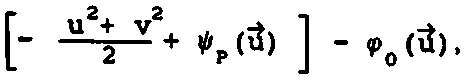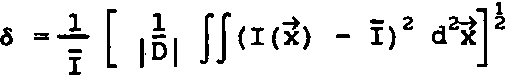Исследование фокусаторов в прямоугольник методом вычислительного эксперимента

• 2.    ПОСТАНОВКА ЗАДАЧИ

• 3.    РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ФОКУСИРОВКИ В ПРЯМОУГОЛЬНИК С ПОСТОЯННОЙ ИНТЕНСИВНОСТЬЮ

Пусть лазерный пуч ок круглого сечения радиуса R, с комплексной амплитудой w_q А- /х₀(3)' e^l^o^{, где I_Q(^) ~ интенсивность освещающего пучка, ^₀(и) - фаза пучка, падает на круглый фокусатор с апертурой G = |(u, v) | u2 + v2s R2j-, расположенный в плоскости i] = (u, v) при z = О (рис. 1), который преобразует падающее излучение в поле w(xt, 0) = = w (u) exp [i}

f где

1(х) = /^’    € ^

(О, иначе, соответствующей равномерно засвеченному прямоугольнику D= [-d; d] х [-d^  d^, где 3-  (x, у) - декартовы координаты в фокальной плоскости.

В работе [3] рассмотрен «метод согласованных прямоугольников* для численного расчета фокусаторов в плоские области. Согласно методу [3], при расчете фокусатора пучка круглого сечения в прямоугольник с постоянной интенсивностью апертура фокусатора G приближается набором апертурных прямоугольников

G^ = [u( t> u(] x Г- VR2- u2', Vr 2 u2 j, i - 1. N, u0 - - R.

• ^u, - R.

прямоугольник фокусировки D представляется набором фокальных пряноугольня-

• D, = [X, _г XJ х [-d^dj. i=l. N, х_о= - d, х„ = d,

прячем разбиение х^ i =1, N определяется из условия сохранения светового потока при распространении света из апертурного прямоугольника Gt в соответствующий фокальный прямоугольник D^

xt = хм+ -^- J J IQ(u, v)du dv, i = 1, N. (1)

• ¹    U               2

l-l -YR - u

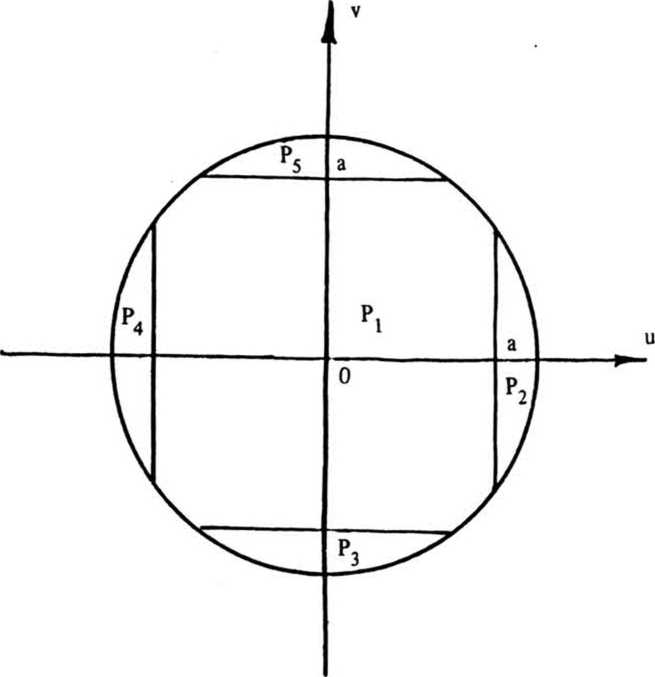
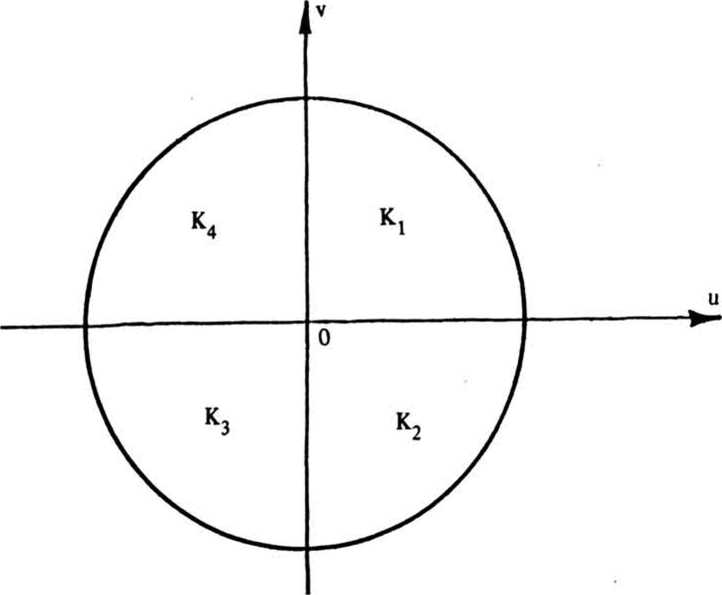
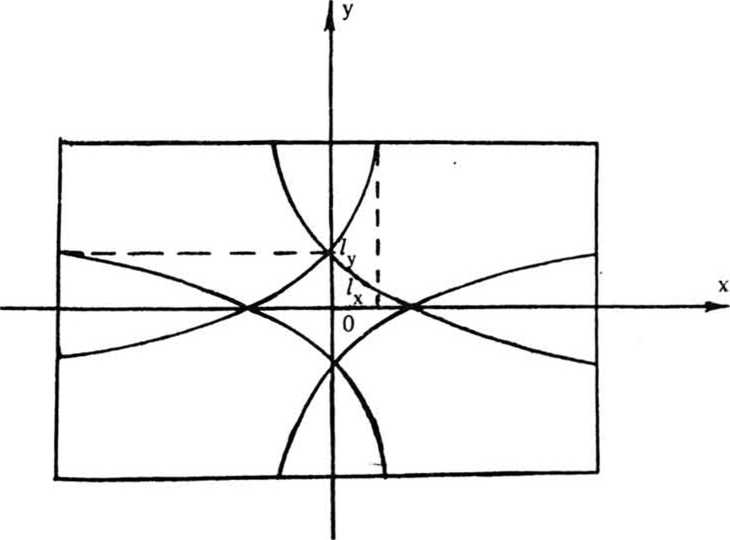
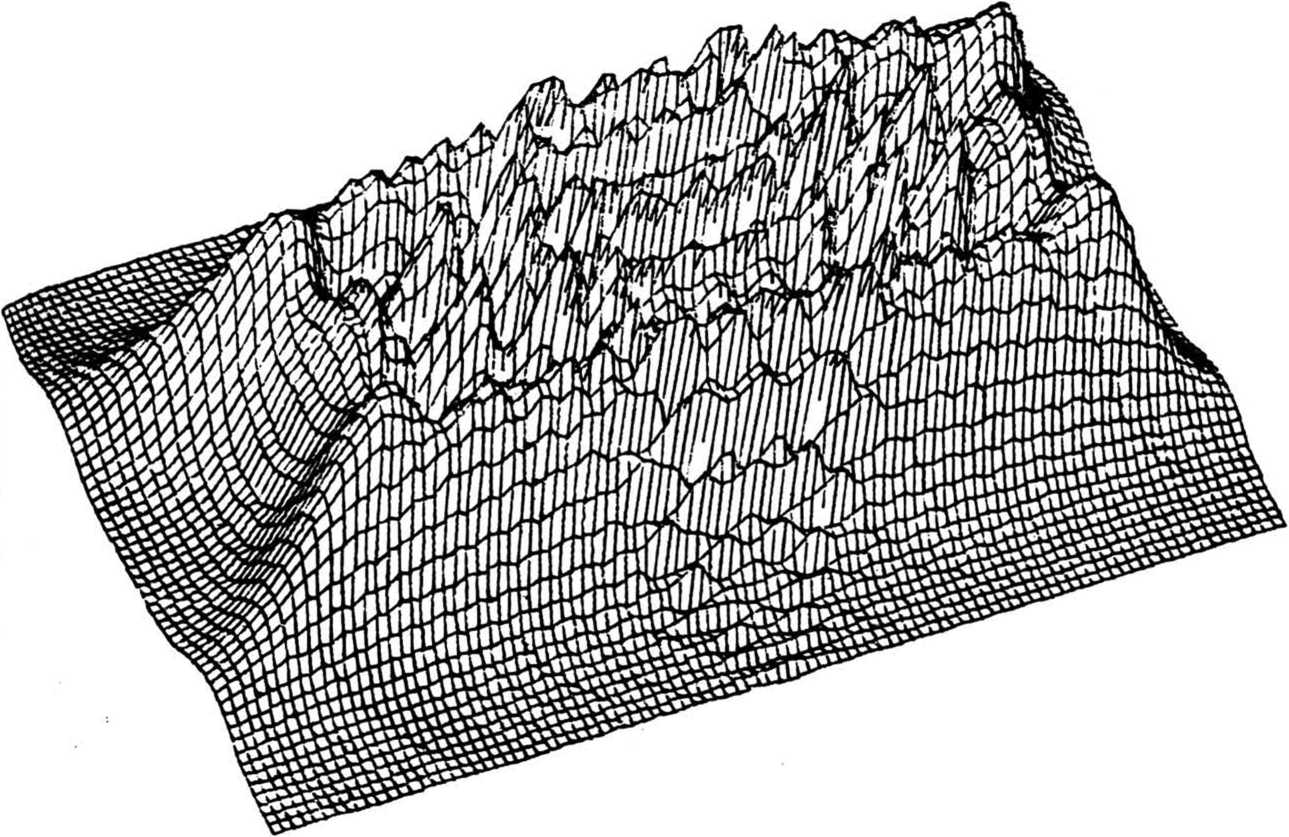
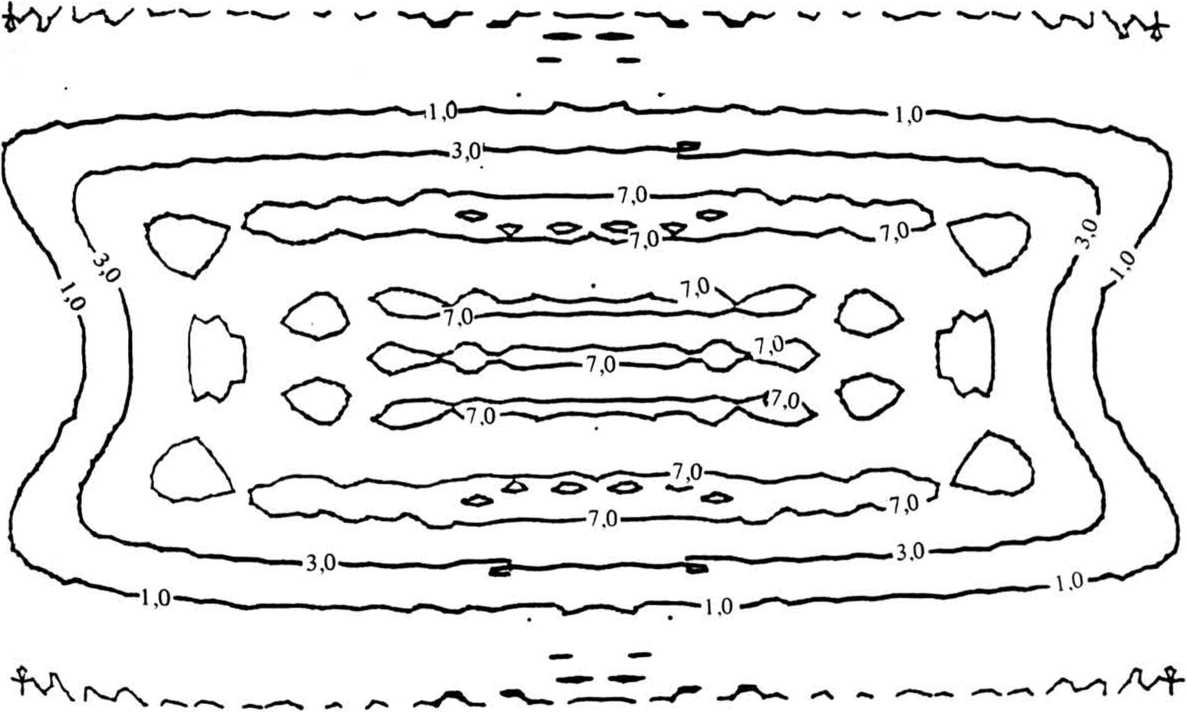
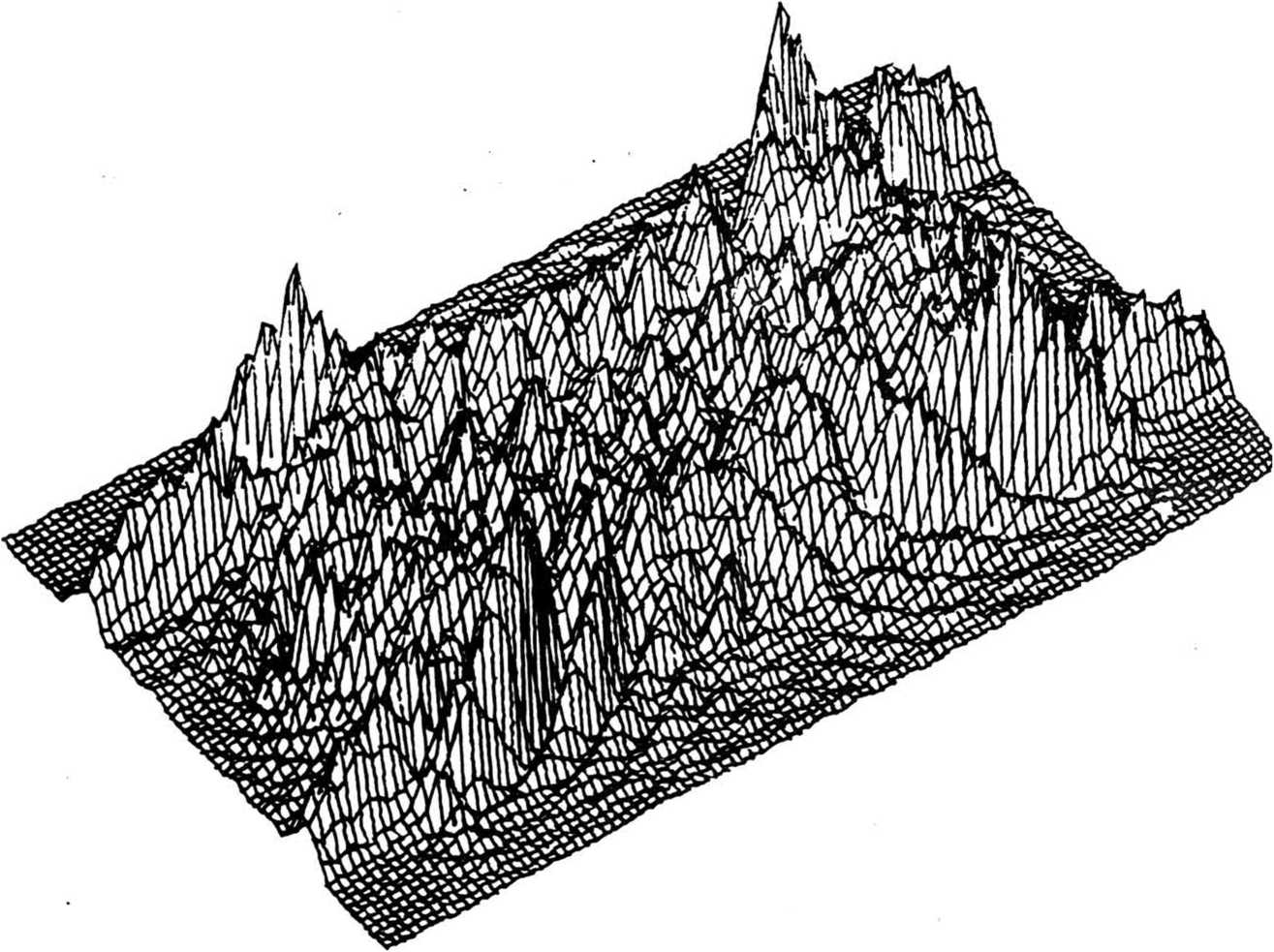
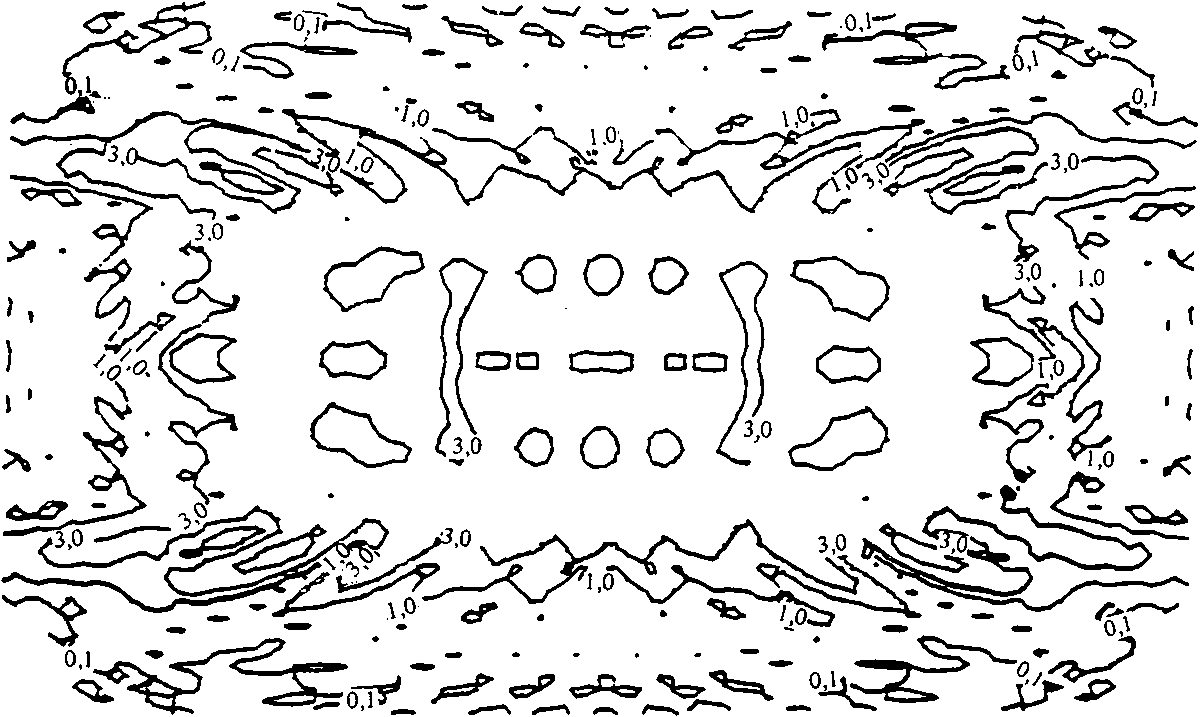
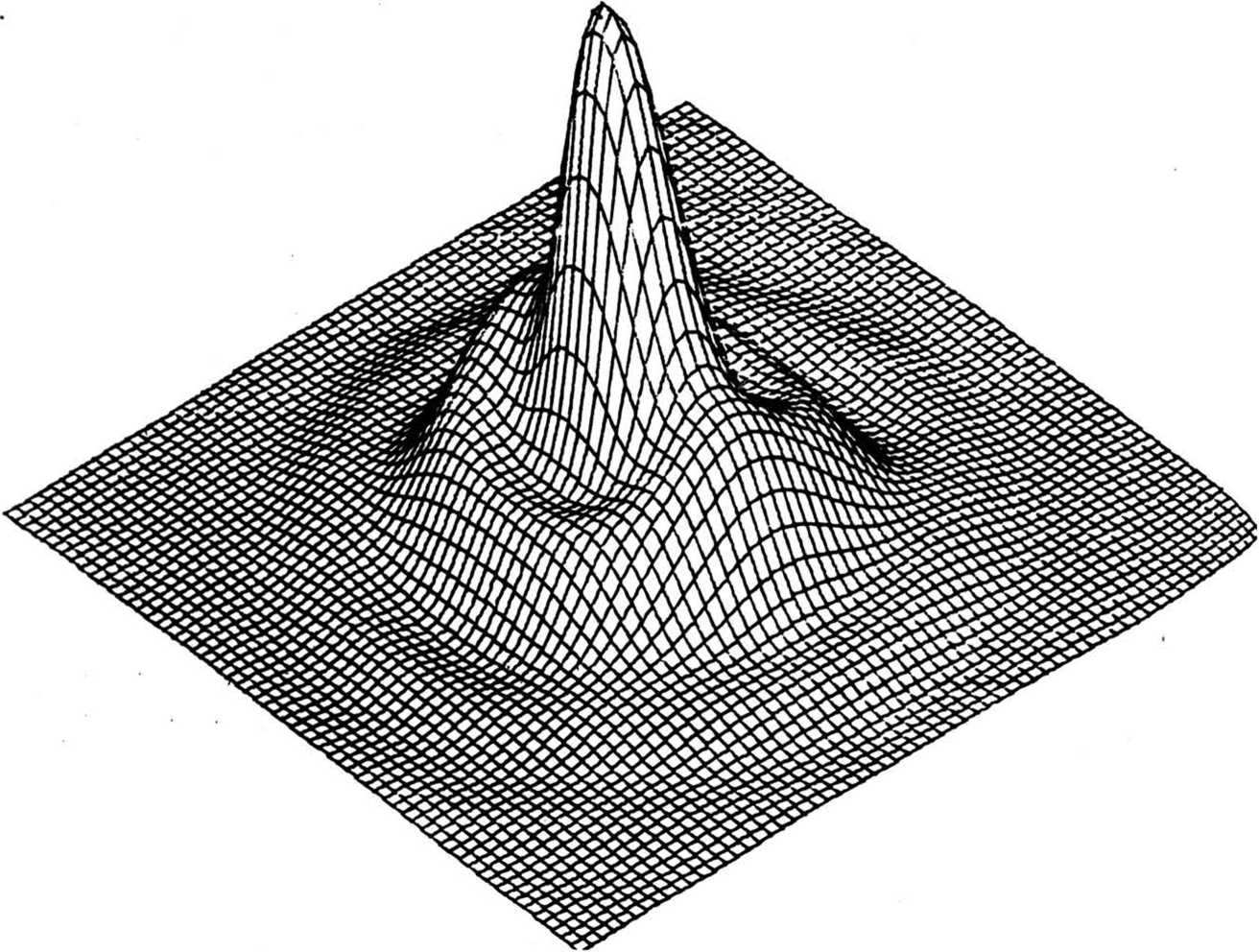
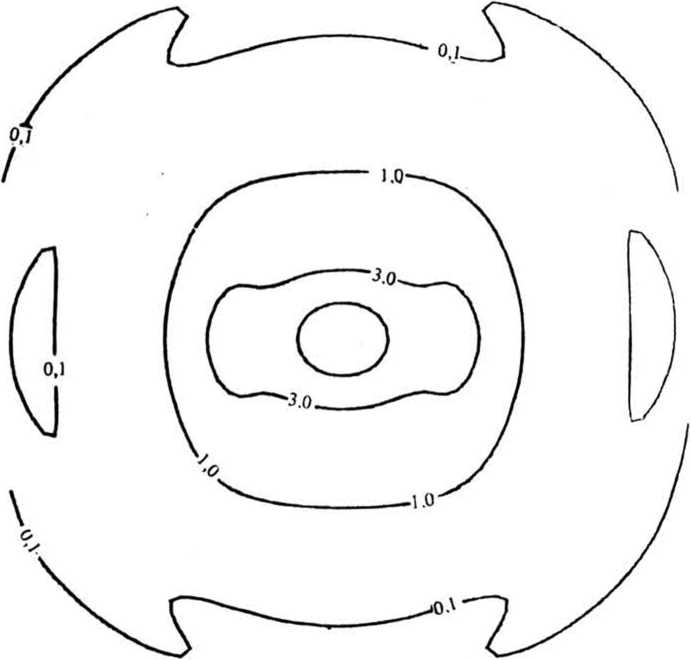
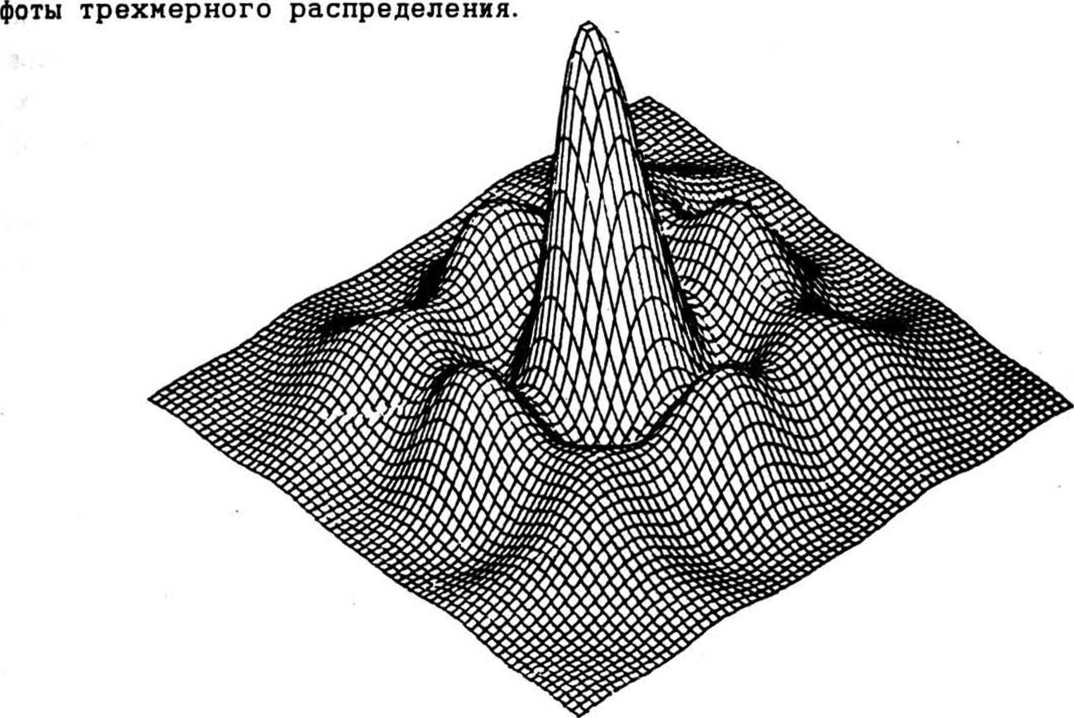
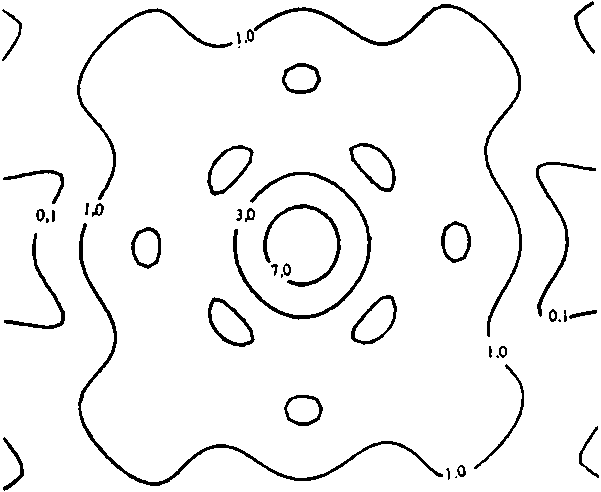
Фазовая функция фокусатора у (x£) имеет вид: .    * г               Г 2u"

р(3) -£[»,(».v) rect [-^-^-J rect [ ^ -] + p,J - ^ ^

где ^(u, v) - фазовая функция сегмента G^ обеспечивающая фокусировку в соответствующий фокальный прямоугольник Dt ;

rect (х) = i1, ^^ 2 'О, иначе ;

фазовая добавка, выбираемая из условия непрерывности у(З) вдоль оси и.

Фазовая функция p(il) терпит разрывы вдоль прямых u=u^ i=l, N.

В предельном случае А и 4 О, N 4 о», из (2) несложно получается непрерывная фазовая функция следующего вида:

Фокусатор (3) будем называть <фокусатором с непрерывной фазовой функцией». В случае гауссового освещающего пучка с комплексной амплитудой _ и

Wo^^~ е       из формулы (3) следует фазовая функция фокусатора 8

прямоугольник, полученная в работе Анализируя геометрооптическое области

1(х,у)

[4] .

распределение интенсивности в фокальной

У^)

можно видеть, что фазовая функция (3) не обеспечивает строго равномерного распределения интенсивности в фокальном прямоугольнике. Поэтому важно проанализировать полученную фазовую функцию в рамках вычислительного эксперимента и сравнить полученный результат с другими способами формирования фокусатора пучка круглого сечения в прямоугольник.

Например, рассмотрим «фокусатор в прямоугольник с сегментами линз>. Освещающий пучок будем считать факторизующимся, wo(u,v) =w01(u) w02 (V), IO(U,V) = I0l(u) I02(v).

Апертуру фокусатора G предполагаем состоящей из сегментов Р , 1=1,5 (рис. 2). Фазовую функцию ф_р (Й) сегмента P_t определим согласно приведенному в работе [3] решению задачи фокусировки факторизуемого пучка квадратного сечения со стороной а в фокальный прямоугольник D с постоянным распределением интенсивности. Такой выбор ф_р (vl) в геометрооптическом приближении обеспечивает фокусировку в фокальную область, близкую к прямоугольнику со сглаженными углами. Поэтому фазовые функции сегментов Р_2> ₽_з> Р^, р$ выбираются из условия фокусировки в точки, лежащие вблизи

Рис. 2. Фокусатор в прямоугольник с сегментами линз

углов фокального прямоугольника D.

Фазовая функция фокусатора в

прямоугольник с сегментами линз имеет вид:

Ф(Й) =

к f

иначе

где а - характерный размер сегмента Р1 .

»р(3) =

(d-eju + (d-ey)v, (d-cx)u - (d^e^v, ueP

ЙеР

з

ЙеР

. 4

^€Ps>

-(d+cju - (d+cy)v,

-(di+cx)ii + (di-ey)v, где с , с - смещения точек фокусировки относительно вершин у фокального прямоугольника.

Конкретные значения а, с*» Су могут быть определены в вычислительном эксперименте из условия лучшего качества фокального распределения интенсивности.

Другой способ формирования фокусатора - «фокусатор в прямоугольник из пересечения эллипсов». Апертуру фокусатора G предполагаем состоящей из четырех секторов круга К, i =1,4 (рис.3). Фазовую функцию каждого сектора определяем из условия фокусировки в смещенную четверть эллипса, что

।

Рис. 3. Фокусатор в прямоугольник из пересечения эллипсов

обеспечивает в геометрооптическом приближении фокусировку в «прямоугольник из пересечения эллипсов» (рис.4). Предполагается, что когда размер прямоугольника фокусировки составляет несколько дифракционных пятен, то из-за дифракционного размытия центральная часть прямоугольника фокусировки окажется заполненной и неравномерность распределения интенсивности будет не слишком велика. Фазовая функция «фокусатора в прямоугольник из пересечения эллипсов» имеет вид:

y(u, v) + J [-d^-du], 3eKt

= ■ ^U1V) + I Cdu-divb 3еКг

^V           а            к                                           (⁵)

ф(и, v) + | [du+d^J,   йеК_з

ф(и, v) + I [-du+d^], ЗеК4, к Г 2+ v2 ^+1      d+1

где ^(и, v) = § - и 1 v ■+ -^ и2+—^v -® (и) - фазовая функция фо- кусатора в эллипс с полуосями d+ly и d+lx, параметры 1х и 1у определяют степень перекрытия частей эллипсов в фокальной области.

Конкретные значения 1,1, обеспечивающие лучшее качество X у фокусировки, также определяются из результатов вычислительного экспери мента.

Рис. 4. Прямоугольник из пересечения эллипсов

использовалось параксиальное

w(x) =

^-“jK^l®^ С

i ф(^)

ехр

> (5-3)]d4

где w(x) - комплексная амплитуда в плоскости фокусировки; у (it) — фазовая функция фокусатора.

Использование даже параксиального приближения интеграла Кирхгофа не позволяет произвести аналитические расчеты поля от рассмотренных фокусато-ров. Поэтому для расчета интеграла (6) использовался численный метод работы [5], реализованный в рамках пакета прикладных программ [6].

Для характеристики качества фокального прямоугольника используются следующие величины: значения энергетической эффективности Е и среднеквадратичного отклонения интенсивности 3.

JJ I(3)d25

Величина Е =    --------- характеризует долю энергии пучка, по-

JJ I0(3)d23

G павшую в область фокусировки. Величина

D

характеризует близость распределения интенсивности 1(х)

к постоянной

Ик^«ч -

Моделирование

величине, где |D| - площадь прямоугольника фокусировки, i = среднее значение интенсивности в области фокусировки.

проводилось для фокусаторов плоского пучка в прямоугольник с размерами d = 8 мм, dt= 4 мм при следующих параметрах: R = 20, 5 мм, f = 800 мм, А = 10, 6 мкм и в квадрат d = d^ 1 мм при R = 9 им, f = 450 мм, Л = 10, 6 мкм.

При фокусировке в прямоугольник 8 х 4 мм вычислительный эксперимент проводился для «фокусатора с непрерывной фазовой функцией» и для «фокусатора в прямоугольник с сегментами линз». Для «фокусатора с непрерывной фазовой функцией» энергетическая эффективность фокусировки составила 85, 6%, а среднеквадратичное отклонение интенсивности - 34,2%.

На рис. 5 представлено трехмерное распределение интенсивности в фокальной области, а на рис.6 - изофоты трехмерного распределения интенсивности. В табл. 1 для «фокусатора в прямоугольник с сегментами линз» приведены значения дифракционной эффективности Е и среднеквадратичного отклонения 3 в зависимости от параметров фазовой функции а,с »Су" Для приведенных параметров наилучшее качество фокусировки Е = 82.2%, 3 = 37,6% достигается при а = 17 мм, с = 0,2 мм, с = 0, 4 мм. На рис. 7 к                     у представлено трехмерное распределение интенсивности от «фокусатора в прямоугольник с сегментами линз», на рис.8 - изофоты трехмерного распределения. Результаты вычислительного эксперимента подтверждают

Рис. 5. Распределение интенсивности в фокальной плоскости "фокусатора с непрерывной фазовой функцией" при фокусировке в прямоугольник 8x4 мм

Рис. 6. Изофоты распределения интенсивности в фокальной плоскости "фокусатора с непрерывной фазовой функцией" при фокусировке в прямоугольник 8x4 мм

Таблица 1

Рис. 7. Распределение интенсивности в фокальной плоскости "фокусатора в прямоугольник с сегментами линз" при фокусировке в прямоугольник 8x4 мм

Рис. 8. Изофоты распределения интенсивности в фокальной плоскости "фокусатора в прямоугольник с сегментами линз" при фокусировке в прямоугольник 8x4 мм работоспособность обоих фокусаторов, но по энергетической эффективности и равномерности предпочтительным является «фокусатор с непрерывной фазовой функцией». При фокусировке в квадрат 1 х 1 мм вычислительный эксперимент проводился для «фокусатора с непрерывной фазовой функцией» и для «фокусатора в прямоугольник из пересечения эллипсов». При указанных параметрах размер стороны квадрата фокусировки составляет всего 47), где 7) = Af/2R - размер дифракционного пятна. Для «фокусатора с непрерывной фазовой функцией» энергетическая эффективность фокусировки составила 77,2%, а среднеквадратичное отклонение интенсивности - 67,1%. На рис. 9 представлено трехмерное распределение интенсивности в фокальной области, а на рис. 10 - изофоты трехмерного распределения. В табл. 2 для «фокусатора в прямоугольник из пересечения эллипсов» приведены значения дифракционной эффективности Е и среднеквадратичного отклонения 5 в зависимос-

Таблица 2

Рис. 9. Распределение интенсивности в фокальной плоскости "фокусатора с непрерывной фазовой функцией" при фокусировке в прямоугольник 1x1 мм

Рис. 10. Изофоты распределения интенсивности в фокальной плоскости "фокусатора с непрерывной фазовой функцией" при фокусировке в прямоугольник 1x1 мм ти от параметра фазовой функции 1^ = 1 , характеризующего степень перекры- частей эллипсов.

тин

Лучшее качество фокусировки Е = 72,6%, S = 64% достигается при

1 =0,5 мм.

На рис. 11 приведено трехмерное распределение интенсивнос-прямоугольник из пересечения эллипсов», на рис.12 - изо-

1 = ти «фокусатора в

Рис. 11. Распределение интенсивности в фокальной области "фокусатора в прямоугольник из пересечения эллипсов" при фокусировке в прямоугольник 1x1 мм

Рис. 12. Изофоты распределения интенсивности в фокальной области "фокусатора в прямоугольник из пересечения эллипсов" в прямоугольник 1x1 мм

Результаты вычислительного эксперимента позволяют сделать вывод, что «фокусатор с непрерывной фазовой функцией» и «фокусатор в прямоугольник из пересечения эллипсов» не позволяют с приемлемым качеством сфокусировать излучение в квадрат, размер стороны которого составляет несколько дифракционных пятен. Таким образом, для расчета фокусаторов в прямоугольник порядка дифракционного размера т? требуется разработка специальных методов, учитывающих дифракционные эффекты. В то же время рассмотренные геометрооптические фокусаторы обеспечивают хорошую фокусировку когерентного излучения в прямоугольник с размерами, в 10 - 100 раз превышающими размер дифракционного пятна.