Исследование формирования протяженного светового пучка с продольной поляризацией с помощью высокоапертурного бинарного аксикона

Последние десятилетия особые типы поляризации электромагнитного излучения активно используются в различных приложениях. Особенно широко применяются так называемые цилиндрические пучки с радиальной и азимутальной поляризацией [1]. Причем особый интерес представляют радиально-поляризованное излучение, т.к. при острой фокусировке такого пучка в фокусе формируется мощная продольная компонента электрического поля.

В связи с поперечным характером распространяющейся плоской волны формирование продольно-поляризованного поля в свободном пространстве некоторое время считалось невозможным. Однако, теперь общеизвестно [2, 3], что любой поперечно ограниченный пучок имеет продольную компоненту даже в свободном пространстве. Разумеется, для параксиальных пучков эта компонента очень слабо выражена, и становится сравнимой с поперечными компонентами только при очень высокой числовой апертуре.

Уникальность радиальной поляризации в том, что она обеспечивает максимальное отношение интенсивности продольной компоненты к интенсивности поперечных компонент при острой фокусировке [4]. Данный эффект используется для уменьшения размеров фокального пятна [5-8], ориентированного изображения молекул [9, 10], генерации второй гармоники [11-13], в спектроскопии [14, 15], а также для ускорения частиц [16-18].

Таким образом, именно актуальность формирования продольно-поляризованного поля Савельев Дмитрий Андреевич, стажёр-исследователь ЛЛИ ИСОИ РАН, аспирант СГАУ.

объясняет повышенный интерес исследователей к радиально-поляризованным пучкам. Заметим, однако, что радиальная поляризация оптимальный, но не единственный способ возбуждения продольной компоненты в фокальной области. При линейной и круговой поляризации лазерные пучки с фазовой сингулярностью также обеспечивают формирование значительной продольной компоненты в режиме острой фокусировки [19-21].

Важным моментом при формировании продольно-поляризованного электрического поля является энергетическая эффективность. Известны оптические схемы, построенные на узкокольцевом диафрагмировании объектива, фокусирующего радиально-поляризованное излучение [5, 6, 22-24]. Это простой и удобный, но низкоэффективный способ формирования длинной (несколько десятков длин волн) продольно-поляризованной иглы.

Более энергетически выгодным является дополнение объектива фазовым дифракционным оптическим элементом [25, 26] или аксиконом [27], в том числе дифракционным [28]. Однако в этом случае световая игла будет длиной не более десятка длин волн.

Эффективный способ формирования протяженного светового пучка с преимущественно продольной поляризацией при освещении асимметричных высокоапертурных бинарных аксиконов линейно-поляризованным излучением был предложен в работе [29]. Было показано, что в этом случае продольно-поляризованный пучок имеет протяженность, пропорциональную радиусу ак-сикона. Это обеспечивает простой способ удлинения пучка без уменьшения его линейной интенсивности. Теоретически бесконечное увеличение входной энергией обеспечивает бесконечную протяженность пучка вдоль оптической оси.

В данной работе исследуется возможность формирования протяженного светового пучка с преимущественно продольной поляризацией при дифракции лазерного излучения на бинарном аксиконе с высокой числовой апертурой. Моделирование выполнено на основе метода конечных разностей во временной области.

1. ДИФРАКЦИЯ ЛАЗЕРНЫХ ПУЧКОВ НА МИКРОАКСИКОНЕ С РАЗЛИЧНЫМ РАДИУСОМ

Рассмотрим высокоапертурный ( а ₀ = 0,95) бинарный микроаксикон вида:

тb (r) = exp|i arg [cos (ka0r) cos (mф)]}. (1)

Для моделирования дифракции различных пучков на аксиконе (1) использовался метод FDTD, реализованный в программном пакете Meep. Расчеты производились с использованием вычислительного кластера мощностью 775 GFlops.

Параметры моделирования: длина волны излучения Я = 0,532 мкм, максимальный радиус аксикона R = 8,6625л, числовая апертура NA = ^а 0 = 0,95. Размер расчётной области x , y , z Е [-9 Я ;9 Я ]. Толщина поглощающего слоя PML со всех сторон окружающего расчетную область - 1,5 Я , шаг дискретизации по простран

ству - Я /40, шаг дискретизации по времени - Я /(80 c ), где c - скорость света. Источник находится на расстоянии 0,1 Я перед рельефом акси-кона, внутри подложки, которая занимает все пространство до PML со стороны, противоположной к рельефу. Время моделирования – 60 временных тактов. Показатель преломления ак-сикона и подложки, в которой выполнен бинарный рельеф вида (1), равен n = 1,5. В этом случае высота микрорельефа составляет:

h =

Я

2(n -1)

= Я

.

В качестве входного пучка рассматривалась мода Гаусса-Лаггера (0,1) с радиусом у = 3,5л:

( )

GL ( r,Ф,z ) = —Г exp [ ikz - i²^(z ) ] exP ( o ( z ) J

inr

exp _ Я ? ( z )J

° ^{2( z )}

exp ( iф ) . (3)

Зафиксировав размер входного пучка, будем варьировать размер рельефа аксикона. Результат моделирования для y-поляризации приведен в табл. 1.

Следует отметить, что уменьшение радиуса рельефа приводит к перераспределению энергии продольной компоненты на оптической оси и уменьшению интенсивности световой иглы.

Так как во многих задачах требуется формирование симметричного пятна, рассмотрим также круговую поляризацию падающего излучения

Таблица 1. Распределение в плоскости YZ [21 Я X 21 Я ], y-линейная поляризация

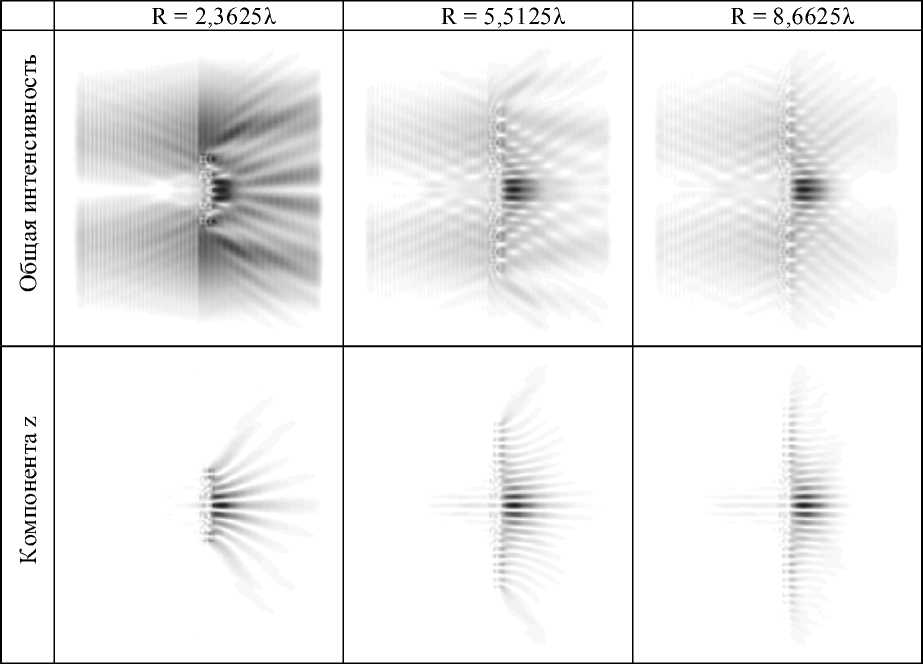
Таблица 2. Распределение в плоскости YZ [21 X X 21 X ], круговая поляризация

R = 2,3625λ R = 5,5125λ R = 8,6625λ л н о о и м к о S к § Н ко О N св Н И CD И о к 2 о « для того же пучка (табл. 2). Будем рассматривать круговую поляризацию, направление которой противоположно направлению вихревой фазовой сингулярности.

Были получены схожие результаты – при фиксированном малом освещении увеличение размеров рельефа приводит к продлению z – компоненты.

2. ДИФРАКЦИЯ ЛАЗЕРНЫХ ПУЧКОВ С РАЗЛИЧНЫМ РАДИУСОМ

В данном разделе рассматривается изменение радиуса светового пучка. Увеличим размер расчетной области, одновременно уменьшив число отсчетов на микрон. Укажем параметры моделирования, которые были изменены: радиус ак-сикона R = 14,9625 X , размер расчётной области x , y , z g [-15,5 X ; 15,5 X ], шаг дискретизации по пространству - X /30, шаг дискретизации по времени - X /(60 c )•

В табл. 3 приведены продольные сечения для моды Гаусса-Лаггера (0,1) с разным радиусом у при y-линейной поляризации. График для общей интенсивности приведен на рис. 1.

Как видно из табл. 3, при увеличении радиуса пучка удлиняется световой фокус, формируемый аксиконом. При этом центральная часть фокального распределения состоит в основном из продольной компоненты (на оптической оси присутствует только z компонента). Таким образом, с помощью высокоапертурного аксикона можно формировать световую иглу, состоящую из продольной компоненты электрического поля. Протяженность этой иглы будет пропорциональна радиусу аксикона, полностью освещенного линейно-поляризованным пучком с вихревой фазовой сингулярностью.

ЗАКЛЮЧЕНИЕ

Проведенные исследования показали возможности формирования протяженного светового пучка с преимущественно продольной поляризацией при дифракции моды Гаусса – Лаггера (0,1) на бинарном аксиконе с высокой числовой апертурой. Моделирование было выполнено на основе метода конечных разностей во временной области.

В работе показана возможность формирования с помощью аксикона, освещенного лазерным пучком с линейной или круговой поляризацией протяженной световой иглы, состоящей из продольной компоненты электрического поля. Это достигается за счет внесения в освещающий пучок вихревой фазовой сингулярности, которая позволяет перераспределять энергию компоненты z, усиливая её интенсивность на оптической оси.

Протяженность световой иглы будет пропор-

Таблица 3 . Распределение в плоскости YZ [34 X X 34 X ], y-линейная поляризация

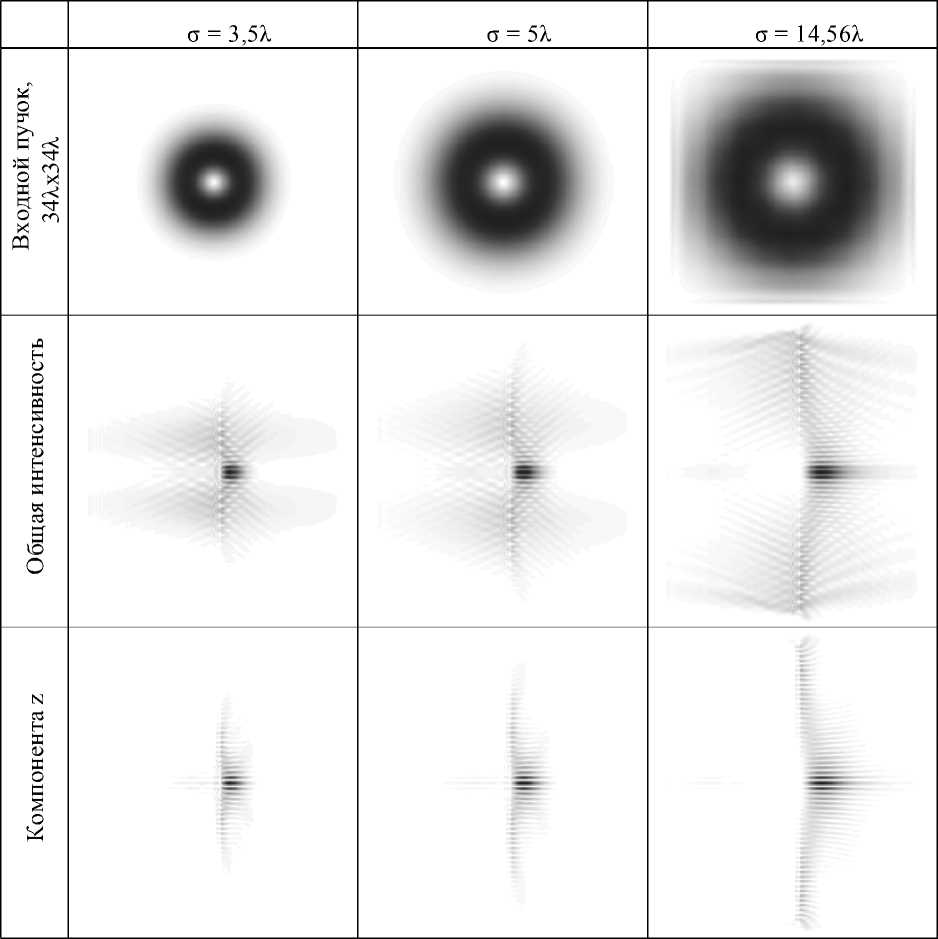
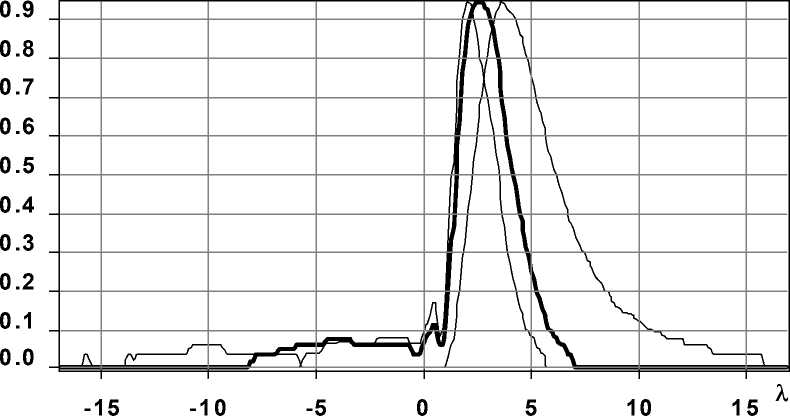
Рис. 1. График продольного распространения общей интенсивности, показано тонкой линией ст = 3,5 X, толстой а = 5 X, пунктиром а = 14,56 X циональна радиусу аксикона, полностью освещенного поляризованным пучком с вихревой фазовой сингулярностью и радиусу лазерного пучка.

Работа выполнена при финансовой поддержке грантов РФФИ 13-07-00266, 14-07-31079 мол_а.