Исследование формирования световых полей с различной скоростью вращения распределения интенсивности

Световые поля с вращающимся при распространении распределением интенсивности могут быть использованы для решения различных прикладных задач [1–5]. В настоящее время одним из наиболее обсуждаемых является их применение для увеличения продольного разрешения флуоресцентных микроскопов [4–5]. Известно, что при получении изображения двух объектов, расположенных в разных плоскостях, но на малом поперечном расстоянии друг от друга выделить информацию об их истинном положении весьма затруднительно. Идея подхода к решению данной задачи на основе световых полей с вращением интенсивности состоит в следующем. Излучение от точечных светящихся объектов в предметной области проходит через оптическую систему микроскопа и специальный фазовый фильтр. По сути, этот фильтр является дифракционным оптическим элементом, который преобразует поле плоской волны в пучок с распределением интенсивности в виде двух вращающихся максимумов (будем называть этот пучок двухлепестковое световое поле). Поэтому в плоскости наблюдения формируются изображения объектов, каждое из которых представляет собой два максимума интенсивности. Оценить продольное смещение объектов друг относительно друга в предметной области можно по изменению положения максимумов интенсивности в плоскости изображения [5]. При этом чем больше скорость вращения интенсивности поля, формируемого дифракционным элементом, тем точнее можно определить продольную координату светящегося объекта. Под скоростью вращения понимается величина, характеризующая угол поворота распределения интенсивности светового поля при распространении в продольном направлении.

Поэтому в данном подходе важной задачей является развитие методов расчёта дифракционных элементов для формирования световых полей с большой скоростью вращения распределения интенсивности.

В данной работе исследуется получение фазовых оптических элементов на основе оптики спиральных пучков света, формирующих световые поля, распределение интенсивности которых поворачивается при распространении. Рассмотрен вопрос о выборе параметров освещающего фазовую маску поля для наиболее эффективного формирования светового поля с вращением интенсивности. Экспериментально определены скорости вращения световых полей для различных параметров. Представлены результаты экспериментов по влиянию аберраций на структуру интенсивности полей.

1.    Световые поля с вращением интенсивности

Спиральные пучки света – световые поля, распределение интенсивности которых сохраняет форму при распространении в свободном пространстве, изменяясь в масштабе и поворачиваясь [6]. Теория спиральных пучков хорошо разработана [6, 7] и позволяет строить световые поля с известным распределением интенсивности и характеристиками поворота при распространении. Угол поворота θ интенсивности спирального пучка в плоскости, расположенной на расстоянии z от исходной, определяется выражением

Г 2 z )

θ ( z ) = θ arctan ,                              (1)

• 0        ( к р ² J

где k – волновое число, ρ – параметр, характеризующий поперечный размер пучка, θ 0 – параметр, определяющий скорость вращения пучка при распространении. Полный угол поворота пучка в зоне Френеля составляет

θ=θ π.

Было показано [7], что в исходной плоскости спиральный пучок можно представить в виде разложения по модам Лагерра–Гаусса

∞∞

F (X, У) = ZZ CnmLGn- lx, yl •

• n = 0 m =-^           ^ ^{р р} J

индексы которых удовлетворяют условию

2n + |m| + 60m = const.

Выбирая значение параметра вращения пучка θ 0 , мы не только задаем скорость вращения пучка, но и определяем его функциональный вид.

С использованием теории спиральных пучков света было реализовано два подхода получения фазовых распределений для генерации двухлепестковых полей с различной скоростью вращения распределения интенсивности. В первом из них исходный спиральный пучок представляет из себя сумму нескольких мод Лагерра–Гаусса, во втором - он получен с помощью функционального представления [8].

В рамках первого подхода были получены фазовые фильтры для формирования полей с параметрами вращения θ 0 =-2 и θ 0 =-4. Для расчёта фазового элемента, формирующего двухлепестковое поле с параметром вращения θ 0 =- 2, был модифицирован алгоритм, описанный в [9]. В качестве нулевого приближения рассматривалась суперпозиция мод Лагер-ра–Гаусса:

F = LG 0,0 + LG 1,₂ + LG 2,4 + LG 3,6 + LG 4,8 . (2)

Далее проводилась корректировка интенсивности рассчитанного поля с целью выделения двух рабочих максимумов и уменьшения шумов между ними, состоящая в проведение прямых и обратных преобразований Френеля между N реперными плоскостями. Одна итерация состоит из N прямых преобразований Френеля в каждую из выбранных плоскостей и N обратных преобразований в плоскость фазового элемента. В нашем случае N=9. После прямого преобразования происходит изменение интенсивности рассчитанного поля по следующему правилу: если интенсивность в данной точке больше, чем 0,5 I max , где I max – максимальная интенсивность, то амплитуда поля не изменяется. В противном случае амплитуда уменьшается в 2 раза. Выход из итерационной процедуры происходит после того, как приращение дифракционной эффективности после i-й итерации составляет менее 5 %.

Фазовый фильтр для светового поля с параметром вращения θ 0 = -4 был получен при использовании спирального пучка вида:

F = LG ₀,₀ + LG 3 2 + LG ₆,₄ . (3)

В рамках второго подхода были получены фазовые распределения для создания двухлепестковых световых полей с параметрами вращения θ 0 = - 1 и θ 0 = -4. Световое поле с θ 0 = - 1 генерировалось с помощью фазового фильтра, содержащего фазу спирального пучка, полученного с помощью функционального представления. Выражение для поля имеет вид:

[ 2 zc |

F ( x , y ,0) = 2 cos      exp

I P2 J

— .  2

zz + c

P ²

где z = x+iy – комплексная переменная, черта обозначает комплексное сопряжение, c – константа.

Фазовый фильтр, содержащий фазу спирального пучка с параметром поворота θ0 = -4, полученного с помощью функционального представления, опреде- ляется выражением:

( zz V z⁵ z³     )

F ⁽ x , y ^,0) = exp l--_? II -5- + c l I ,                ⁽⁵⁾

I p Л p J

где c 1 – константа. Исследуемое поле экспериментально формировалось при освещении данного фазового фильтра равномерным по интенсивности пучком с плоским волновым фронтом.

Проведено численное моделирование по выбору оптимальной величины радиуса круговой апертуры при различных типах освещения фазового элемента. Было показано, что при однородной засветке фазовой маски, полученной итерационным способом, наибольшая эффективность формирования наблюдается при радиусе апертуры R a = 4ρ (рис. 1). Под энергетической эффективностью понимается отношение энергии в главных вращающихся долях (максимумах интенсивности) к полной энергии в данном сечении. Для световых полей, полученных с помощью функционального представления, тоже проводилось моделирование по выбору величины апертуры. Экспериментальная проверка его результатов показала, что наиболее эффективно световые поля (4) и (5) формируются в том случае, когда ширина освещающего пучка совпадает с шириной видимой интенсивности исходного спирального пучка.

0,5a     0,6a     0,7a     0,8a     0,9a     1,0a

Рис. 1. Подбор размера апертуры для поля, созданного на основе суперпозиции мод Лагерра–Гаусса с параметром вращения θ 0 = - 2. Параметр a = 2R a = 8ρ. Верхний ряд – распределения фазы при различных апертурах; нижний ряд – соответствующие распределения интенсивности (негатив)

2.    Экспериментальная реализация исследуемых световых полей с вращением интенсивности

Экспериментальная реализация световых полей осуществлялась с помощью фазового пространственного ЖК-модулятора HOLOEYE HEO-1080. Расширенный, коллимированный, однородный по интенсивности пучок от твердотельного лазера (мощность до 50 мВт, λ = 532 нм) направлялся на модулятор HOLOEYE HEO-1080, на котором создавалось фазовое распределение исследуемого светового поля. После дифракции излучения на модуляторе формировалось исследуемое поле, которое фокусировалось линзой с фокусным расстоянием 30 см, вписанной в фазовое распределение. Анализ распределения интенсивности исследуемых полей в различных сечениях производился с помощью горизонтального микроскопа и цифровой камеры. Схема экспериментальной установки приведена на рис. 2.

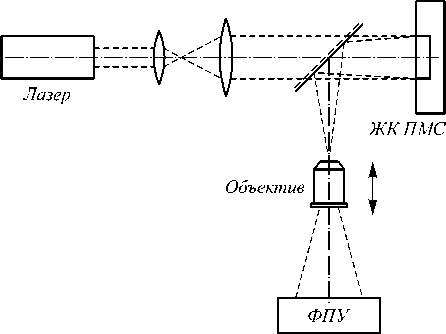
Рис. 2. Экспериментальная установка

В эксперименте фазовый элемент освещался однородным полем, апертура которого соответствует наиболее эффективному формированию распределения интенсивности. Распределения интенсивности регистрировались в плоскостях, перпендикулярных направлению распространения исследуемого светового поля, расположенных на расстоянии 2 мм друг от друга. Угол поворота полученных распределений интенсивности определялся по отношению к исходному распределению (оценивался угол отклонения от горизонтали). На основании этих результатов была построена зависимость угла поворота распределения интенсивности от расстояния до плоскости фокусировки. На рис. 3 приведены экспериментально полученные распределения интенсивности для двухлепестковых световых полей, созданных на основе спиральных пучков с параметрами вращения θ 0 =- 1, θ 0 =-2 и θ 0 =-4.

Графики зависимости угла поворота распределения интенсивности от расстояния до плоскости фокусировки двухлепестковых световых полей с параметрами вращения θ 0 =- 1 и θ 0 =-2 приведены на рис. 4. Аналогичные графики для двухлепесковых световых полей с параметром поворота θ 0 =-4 приведены на рис. 5. Результаты эксперимента показывают, что полученные для двухлепестковых полей зависимости угла поворота согласуются с теоретической зависимостью угла поворота (1) для параметров вращения θ 0 =- 1, θ 0 =-2 и θ 0 =-4. Также из графика видно, что при данных параметрах экспериментальной установки световые поля с θ 0 =-4 на линейном участке графика имеют скорость вращения 16°/мм для светового поля, полученного с помощью функционального представления, и 13°/мм для светового поля, представляющего собой суперпозицию мод Лагерра–Гаусса (3). Световое поле с θ 0 =-2 на линейном участке графика имеет скорость вращения 7°/мм, это значение скорости в два раза меньше, чем для полей с θ 0 =-4. Скорость поворота для поля с θ 0 =- 1 на линейном участке составляет 3,5°/мм, что в два раза меньше, чем для полей с θ 0 =-2, и в четыре раза меньше, чем для поля с θ 0 =-4. Полученные результаты согласуются с теоретическими расчётами.

Была измерена энергетическая эффективность формирования данных полей. Эффективность форми- рования для поля с параметром вращения θ0=- 1 составила 50 %; для поля с параметром вращения θ0=-2 – 56 %; для поля (5) – 30 %; для поля с параметром вращения θ0=-4, полученного на основе суперпозиции мод Лагерра–Гаусса (3), – 27 %.

интенсивности для двухлепесткового поля: а) с параметром поворота θ 0 = - 1; б) с параметром поворота θ 0 = - 2;

в) с параметром поворота θ 0 = - 4 , представляющего собой суперпозицию мод Лагерра–Гаусса; г) с параметром поворота θ 0 = - 4, полученного с помощью функционального представления (приведены негативы)

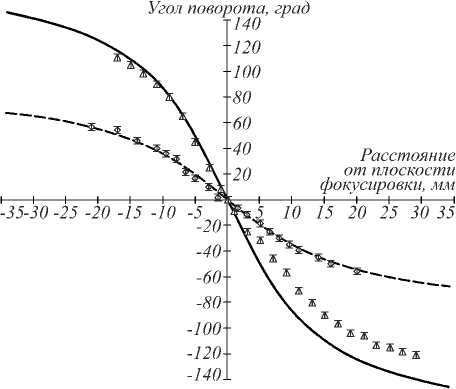
Рис. 4. Графики зависимости угла поворота распределения интенсивности двухлепестковых полей с параметрами поворота θ 0 = - 1 и θ 0 = - 2, от расстояния до плоскости фокусировки. Сплошная линия – аналитическая зависимость (1) для θ 0 = - 2, ромбы – экспериментально полученные точки для светового поля (4). Пунктирная линия – зависимость (1) для θ 0 = - 1, треугольники – экспериментальные точки для светового поля с θ 0 = - 2, полученного с помощью итерационного процесса. Ошибка измерения составила 5°

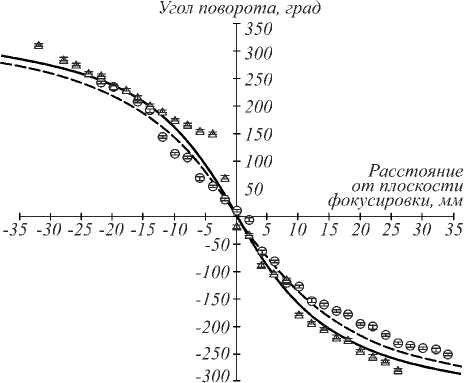
Рис. 5. Графики зависимости угла поворота распределения интенсивности двухлепестковых световых полей, созданных на основе спиральных пучков с параметром поворота θ 0 = - 4, от расстояния до плоскости фокусировки. Сплошная линия соответствует зависимости (1) для θ 0 = - 4. Треугольники – экспериментальные точки, полученные для светового поля с θ 0 = - 4, полученного с помощью функционального представления. Пунктирная линия – зависимость (1) с коэффициентами, подобранными для круглых экспериментальных точек. Круги – экспериментальные точки для светового поля с θ 0 = - 4, представляющего собой суперпозицию мод Лагерра–Гаусса.

Ошибка измерения составила 5°

В работе было исследовано влияние первичных аберраций, таких как кома, астигматизм и сферическая аберрация на формирование двухлепестковых световых полей с вращением. Эти аберрации представляют интерес, так как могут возникнуть в оптической системе микроскопа. Искажения, вносимые данными аберрациями, могут полностью «испортить» формируемое поле и привести к потере информации о положении долей двухлепестковых полей. Важно знать, при какой величине аберрации еще можно различить две доли в рас- пределении поля и верно определить их ориентацию. Была проведена серия экспериментов по формированию двухлепестковых световых полей с первичными аберрациями (сферическая, кома, астигматизм) различной величины (λ/32, λ/16, λ/8, λ/4, λ/2, λ). В этих экспериментах фазовое распределение, подающееся на пространственный модулятор света, представляло собой сумму фазового распределения исследуемого поля и аберрации. Аберрации формировались в представлении полиномов Цернике [10] в соответствии с нормировкой стандарта OSA [11].

I NR ( r ) cos( m 6 ), для m - 0; z m ( r , 6 ) =1

[- N m R m ( r ) sin( m 6 ), для m <  0.

⁽ n ^-| m )/2                      s

R m ( r ) = Z     ₍ ।⁽| )(r )!

s=0    [ n + m If n - s!           - s !

- rn ^{- 2} s ;

!

N n^m

1 2( n + 1)

У ¹ +8 _m 0

где r и θ – полярные координаты. Переменная r изменяется в пределах [0, 1]. При расчёте фазовой маски производилось масштабирование радиальной координаты так, чтобы радиус апертуры был равен единице. Аберрации задавались в виде: Z 2² – астигматизм, Z 3¹ – кома, Z 4⁰ – сферическая аберрация.

Регистрировались распределения интенсивности в нескольких плоскостях, перпендикулярных оси распространения светового поля. В ходе визуального анализа экспериментальных распределений интенсивности исследуемых световых полей с аберрациями было установлено, что при величине сферической аберрации λ/16, комы λ/16 и астигматизма λ/8 из распределения интенсивности исследуемых световых полей ещё можно извлечь информацию о положении долей поля. Полученные распределения интенсивности в одном из сечений для светового поля с параметром вращения θ 0 =-4 в виде (3) приведены на рис. 6. Аналогичные картины получались для двухлепестковых полей с другими параметрами вращения.

Рис. 6. Распределения интенсивности для двухлепесткового поля с параметром поворота θ 0 = - 4, представляющего собой суперпозицию мод Лагерра–Гаусса (2) с аберрациям: а) со сферической аберрацией; б) комой; в) астигматизмом. Величина аберрации (слева направо) 0 (поле без аберрации), λ/32, λ/16, λ/8, λ/4

Заключение

В работе представлены результаты численного моделирования и экспериментальной реализации с помощью ЖК ПВМС HOLOEYE HEO-1080P двухлепестковых световых полей с различной скоростью вращения. С помощью численного моделирования найдены параметры освещающего фазовую маску поля для наиболее эффективного формирования исследуемых световых полей, которые использовались при экспериментальной реализации. Полученные результаты позволяют сделать вывод о том, что скорость вращения возрастает с увеличением параметра вращения прямо пропорционально его величине. Для полей с параметром вращения θ 0 =-4 она составила 16°/мм для поля (5) и 13°/мм для поля, сформированного на основе суперпозиции мод Лагер-ра–Гаусса (3). Отметим, что с увеличением θ 0 падает энергетическая эффективность сформированных полей.

Для полученных экспериментально световых полей с максимальной скоростью вращения она не превышала 30%, а для случая θ 0 =-2 достигала максимального значения в 56 %. Повышение эффективности формирования важно для успешного применения этих полей для задач повышения разрешения в продольном направлении флуоресцентных микроскопов.

Проведён ряд экспериментов, посвященных исследованию влияния комы, астигматизма и сферической аберрации на двухлепестковые световые поля. Установлено, что при величине сферической аберрации λ/16, комы λ/16 и астигматизма λ/8 из распределения интенсивности исследуемых световых полей с вращением ещё можно извлечь информацию об угловом положении долей поля.

Работа выполнена при поддержке Программы фундаментальных исследований ОФН РАН «Фундаментальные основы и экспериментальная реализация перспективных полупроводниковых лазеров в интересах промышленности и технологий» и при поддержке гранта Учебно-научного комплекса ФИАН (УНК).