Исследование функций роста в конечных двупорожденных группах периода 5

Пусть B ₀ (2, 5, k ) – максимальная конечная двупо-рожденная бернсайдова группа периода 5 ступени нильпотентности k . В данном классе групп наибольшей является группа B ₀(2,5,12), порядок которой равен 5³⁴ [1]. Положим { a ₁, a ₂} – порождающие элементы B ₀(2,5, k ) .

В [2] было начато исследование функций роста в группах B ₀(2, 5, k ) . Относительно порождающего множества { a ₁, a ₁ ^{- 1} a ₂, a ₂ ^{- 1}} вычислены указанные характеристики групп для k ≤ 5 .

Настоящая работа является логичным продолжением [2]. В ней будут представлены результаты вычислений функций роста указанных групп для порождающего множества Α= { a ₁, a ₂} при k ≤ 5 . Функция роста группы B ₀(2,5,6) относительно Α получена К. А. Филипповым в работе [3].

Для вычисления функции роста и диаметра графа Кэли относительно Α необходимо перечислить все элементы группы в формате минимальных слов [4]. Вычислив количество слов на каждой длине, можно будет получить функцию роста группы, а максимально возможная длина минимальных слов будет являться диаметром Кэли группы.

Отметим, что для случаев k = 2, 3, 4, 5 были использованы компьютерные вычисления, основанные на алгоритме из разд. 1.

Рассматриваемая задача помимо фундаментального значения, имеет также и приложения, например, при проектировании компьютерных вычислительных сетей [5]. Сеть процессоров может быть представлена как неориентированный граф, в котором процессоры являются вершинами, а две вершины графа соединены ребром, если имеется прямое соединение между соответствующими процессорами. С одной стороны, желательно, чтобы между процессорами было как можно меньше соединений, а с другой, обмен данными между процессорами предпочтительно производить с наименьшим числом посредников. Очевидно, эти два критерия противоречат друг другу. На теоретико-групповом языке диаметр графа вычислительной сети будет равен максимальной длине минимальных слов соответствующей графу группы.

Описание алгоритма вычисления функции роста группы. Пусть p – простое число, а G – конечная группа экспоненты p . Это значит, что g^p = 1 для всех g ∈ G . Положим Α = { a ₁, a ₂} – порождающие элементы G . На множестве Α введем отношение порядка « <» (меньше): a ₁ ≺ a ₂. Пусть g элемент из G . Тогда его можно представить в виде конечного произведения из порождающих, т. е. , g =α ₁ ⋅α ₂ ⋅ ... ⋅α _s , где α _i ∈Α , правую часть данного равенства мы будем называть словом и записывать v =α ₁ α ₂... α _s . Натуральное число s будем называть длиной слова v .

Функция L ( v ) определена на множестве всех слов и равна длине слова v , т. е. L ( v ) = s для слова v , указанного выше. Единица группы e будет представлена пустым словом, которое мы будем обозначать ε . По определению, длина пустого слова равна 0.

Определение отношения порядка на множестве слов. Будем говорить, что слово v меньше слова w и записывать это как v ≺ w , если имеет место одно из следующих утверждений:

• 1.    L ( v ) <  L ( w );

• 2.    Если L ( w ) = L ( v ), тогда пусть v = a ₁ a ₂... a ₅ и w =P j P 2 ... P 5 , a =P i , ^a 2 = P 2 , ^a k - i =P k _ i , ^a k ^ P k для некоторого 1 <  k <  5 .

Определение минимального слова . Слово v будем называть минимальным в G относительно введенного порядка, если для любого другого слова w , удовлетворяющего условию g_v = g w , будет выполняться v ≺ w .

Так как G нильпотентна, то мы можем найти цепочку подгрупп G i (1 <  i <  n ), обладающих следующими свойствами:

G = G1 ^ G2 ^...^ Gn ^ Gn+1 = e,

G i нормальны в G , а факторы G i / G_{i + 1} имеют порядок p и лежат в центре G / G_{i + 1} .

Пусть для 1 < i < n элемент ai е Gi, но ai е Gi+1, тогда каждый элемент группы g е G может однозначным образом записан в виде g = л' а22 ann ,0 <уi < p. (1.1)

Такое представление элементов группы (pc-представление), можно получить при помощи алгоритма известного как p-quotient algorithm [6]. Он реализован в системах компьютерной алгебры GAP и Magma. Если A - порождающее множество группы G , то любой ее элемент, записанный в виде слова а₁ а ₂ _ а₅ , где a i е A , можно преобразовать к виду (1):

pq

а₁ а ₂ ... а₅ ^ а / ¹ а 22 ... a n ⁿ . ( 2)

Процедура (2) дает возможность решить проблему равенства слов в G . На ее основе мы можем перечислить элементы G в формате минимальных слов.

Обозначим через K_s ( G ) множество всех минимальных слов группы G , не превосходящих по длине s . Множество Q_s ( G )– элементы K_s ( G ), записанные в виде правой части (2). Пустое слово – единицу группы обозначим e .

Пусть 5 ₀ е N - минимальное число, для которого выполняется K₅ 0 ( G ) = K₅ 0 _{+ 1}( G ). В этом случае 5 ₀ будет являться диаметром Кэли группы G . Опишем алгоритм, вычисляющий K_s :

• 1.    5 = 0, K 0 = { е }, Q o = { e }, T = K 0 .

• 2.    5 = 5 + 1, K = K - 1 , Q_s = Q_s - 1 , V = а 1 T U а 2 T , T = 0 , i = 1.

• 3.    Для v i е V   v i ^ w .   Если w е Q₅ , то

• 4.    Если <

• 5.    Если <

• 6.    Диаметр G равен 5 - 1, K_{5 - 1}( G ) - множество всех минимальных слов группы. Функция роста задается формулой f ( j ) = | K j ( G ) | - 1 K j _{- 1} ( G ) | (1 <  j <  5 - 1).

• 7.    Завершение работы алгоритма.

pq

K = K U v i , Q 5 = Q 5 U w , T = T U v i .

[ i <  V I, то i = i + 1, переход в3;

I i = V |, то переход в 5.

\ T ^ 0 , то переход в пункт 2;

| T = 0 , то переход в пункт6.

Группа B ₀(2,5,1). Данная группа представляет собой элементарную абелеву группу, порядок которой равен 5² . Нетрудно вычислить функцию роста данной группы и диаметр Кэли (см. табл. 1). Справедлива следующая

Теорема 1. Относительно порождающего множества A группа B ₀ (2,5,1) имеет диаметр Кэли, равный 8, а функция роста задана табл. 1.

Доказательство. Очевидно.

Таблица 1

Функция роста группы B ₀(2,5,1)

Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов
0	1	3	4	6	3
1	2	4	5	7	2
2	3	5	4	8	1
|B 0 (2,5,1)| = 5 2 = 25

Группа B ₀(2,5, 2). Любой элемент группы B ₀(2,5,2) представим в виде нормального коммутаторного слова [1]:

g = ^ ^а 2 2 ^а 3 3 , у i ^е Z 5 .

Для умножения элементов, будем использовать полиномы Холла, полученные в [7].

Пусть a ₁ ^{x 1} a ₂ ^{x 2} a ₃ ^{x 3} и a ₁ ^{y 1} a ₂ ^{y 2} a ₃ ^{y 3} – два произвольных элемента в группе B ₀(2,5,2), записанных в коммутаторном виде. Тогда их произведение равно а ^ ¹ а 2 Х ² а 3 ³ • а ^¹ а У ² а 3' ³ = а ₁ ^ч а 2 ² а ^z z ³ , где z i е Z ₅ и:

z1 = x1 + У1, z 2 = x 2 + y 2, z 3 = x3 + У 3 + x 2 У1.

Применив алгоритм из разд. 1, получим функцию роста рассматриваемой группы (табл. 2).

Имеет место

Теорема 2. Относительно порождающего множества A группа B ₀(2,5,2) имеет диаметр Кэли, равный 10, а функция роста задана табл. 2.

Доказательство. Следует из вычислений функции роста группы B ₀(2,5,2) по алгоритму из разд. 1.

Таблица 2

Функция роста группы B ₀(2,5,2)

Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов
0	1	3	8	6	23	9	10
1	2	4	15	7	21	10	4
2	4	5	20	8	17
1 B o (2,5,2)| = 5 3 = 125

Таблица 3

Функция роста группы B ₀(2,5,3)

Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов
0	1	6	56	12	487	18	12
1	2	7	100	13	438	19	4
2	4	8	166	14	343	20	2
3	8	9	262	15	222
4	16	10	370	16	112
5	30	11	455	17	34
| B o (2,5,3)| = 55 = 3125

Группа B0(2,5,3). Каждый элемент группы B0(2,5,3) представим в виде нормального коммутаторного слова g = a^ a22 a33 a44 a55, уi e Z5.

Пусть a ₁ ^{x 1} a ₂ ^{x 2} a ₃ ^{x 3} a ₄ ^{x 4} a ₅ ^{x 5} и a ₁ ^{y 1} a ₂ ^{y 2} a ₃ ^{y 3} a ₄ ^{y 4} a ₅ ^{y 5} – два произвольных элемента в группе B ₀(2,5,3) , записанных в коммутаторном виде. Тогда их произведение равно a ₁ ^{x 1} a ₂ ^{x 2} a ₃ ^{x 3} a ₄ ^{x 4} a ₅ ^{x 5} ∙ a ₁ ^{y 1} a ₂ ^{y 2} a ₃ ^{y 3} a ₄ ^{y 4} a ₅ ^{y 5} = a ₁ ^{z 1} a ₂ ^{z 2} a ₃ ^{z 3} a ₄ ^{z 4} a ₅ ^{z 5} , где z i ^e Z 5 и:

zi = x + У1, z 2 = x 2 + y 2 , z 3 = x3 + y 3 + x 2 У1,

Группа B ₀(2,5, 4). Каждый элемент группы

B0(2, 5, 4) представим в виде нормального коммута- торного слова g = a/1 a22 a33 a44 a55 a66 a 77 a88, уi e Z5.

Пусть             a1x1 a2x2 a3x3 a4x4 a5x5 a6x6 a7x7 a8x8             и a1y1 a2y2 a3y3 a4y4 a5y5 a6y6 a7y7 a8y8 – два произвольных элемента в группе B0 (2, 5, 4) , записанных в коммутаторном виде.     Тогда их произведение равно a1x1a2x2a3x3a4x4a5x5a6x6a7x7a8x8∙ a1y1a2y2a3y3a4y4a5y5a6y6a7y7a8y8= az a22 a33 a44 a55 a66 a77 a88, где zi e Z5 и:

zi = xi + У1, z 2 = x 2 + y 2 , z3

= x 3 + y 3 + x 2 У 1 ,

z ₅

, I У 1 I, z 4 = x 4 ⁺ У 4 ⁺ x 2 I 2 I ⁺ x 3 У 1 ,

Z ₄ = x ₄

⁺ У 4 ⁺ x 2

У 1 L ₂ I ^{+ x} 3 У 1 ,

I x 2 I

= x 5 + y 5 + x 2 У 1 У 2 + I 2 I У 1 + x 3 У 2 .

z 5 = x 5 + y 5

I X 2 I

^{+ x} 2 У 1 У 2 ⁺I 2 I У 1 ^{+ X} 3 У 2 ,

Здесь и далее I I = —-—:— --биномиальный ко-

I r ) r!(n - r)!

z 6 = ^x 6 ⁺ у 6

. I У1 I . I У1 I .

+ X2 I 3 I+ X3 I 2 I + X4У1, эффициент. Применив алгоритм из разд. 1, вычислим функцию роста группы B0(2,5,3) (табл. 3).

Справедлива следующая

Теорема 3. Относительно порождающего множества А группа B 0 (2,5,3) имеет диаметр Кэли, равный 20, а функция роста задана таблицей 3.

Доказательство. Следует из вычислений функции роста группы B ₀(2,5,3) по алгоритму из разд. 1.

Z 7 — X 7 + У 7

I X2 II У1 1 I У1 I

+         + x? У? +

22     222

^{+ x} 3 У 1 У 2 ^{+ X} 4 У 2 ^{+ X} 5 У 1 ,

I X 2 I I X 2 I z 8 = x8 + У 8 +I 3 I У1 +I 2 I У1У 2 +

^{+ x} 2 У 1

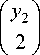
+ x ₃

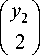
^{+ X} 5 У 2 .

Применив алгоритм из разд. 1, найдем функцию роста группы B ₀(2,5,4) (табл. 4).

Теорема 4. Относительно порождающего множества А группа B 0 (2,5,4) имеет диаметр Кэли, равный 30, а функция роста задана таблицей 4.

Доказательство. Следует из вычислений функции роста группы B ₀(2,5,4) по алгоритму из разд. 1.

Группа B ₀(2,5,5). Аналогичным образом вычислим функцию роста группы B ₀(2,5,5) (табл. 5).

Справедлива следующая

Теорема 5. В алфавите А группа B 0 (2,5,5) имеет диаметр Кэли, равный 32, а функция роста задана таблицей 5.

Доказательство. Следует из вычислений функции роста группы B ₀(2,5,5) по алгоритму из разд. 1.

Группа B ₀(2,5,6). К. А. Филиппов в работе [3] вычислил функцию роста группы B ₀(2,5,6) (табл. 6).

Таблица 4

Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов
0	1	8	214	16	21923	24	18448
1	2	9	410	17	31600	25	8706
2	4	10	784	18	41954	26	3256
3	8	11	1487	19	50670	27	812
4	16	12	2735	20	54460	28	152
5	30	13	4905	21	51399	29	52
6	58	14	8529	22	42862	30	26
7	112	15	14118	23	30892
IB 0(2,5,4) = 5 8 = 390625

Таблица 5

Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов
0	1	9	410	18	126828	27	887095
1	2	10	784	19	229180	28	487974
2	4	11	1495	20	399742	29	179463
3	8	12	2845	21	658283	30	36089
4	16	13	5409	22	994274	31	3332
5	30	14	10271	23	1332692	32	116
6	58	15	19476	24	1533785
7	112	16	36732	25	1497003
8	214	17	68679	26	1253223
| B 0(2,5,5)| = 510 = 9765625

Таблица 6

Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов	Длина	Кол-во слов
0	1	12	2847	24	6055431	36	831332170
1	2	13	5417	25	11319139	37	618248452
2	4	14	10303	26	21039700	38	367604796
3	8	15	19602	27	38795471	39	151894200
4	16	16	37254	28	70686385	40	34898104
5	30	17	70751	29	126432849	41	3181218
6	58	18	134224	30	219647100	42	69158
7	112	19	254321	31	364201879	43	800
8	214	20	481252	32	561801464	44	316
9	410	21	909349	33	779044350	45	158
10	784	22	1714866	34	936055279
11	1495	23	3226931	35	954336955
B 0(2,5,6) = 5 14 = 6103515625

Функция роста группы B ₀(2,5,4)

Функция роста группы B ₀(2,5,5)

Функция роста группы B ₀(2,5,6)