Исследование гидродинамики смазки в зазорах механизма газораспределения двигателя внутреннего сгорания

DOI:

При проектировании и исследовании механизма газораспределения (МГР) ДВС большое внимание в последнее время уделяется

гидродинамике смазки в зазорах. Это вызвано заметным ее влиянием на динамику механизма, широким использованием различных гидроэлементов в клапанном приводе, а также необходимостью определения трибологических характеристик основных сопряжений МГР, в значительной мере определяющих его надежность [3–6]. В связи с этим в данной работе представлена обобщенная методика математического моделирования динамики МГР с учетом гидродинамики смазки, а также приведены некоторые результаты ее использования.

При сближении контактирующих поверхностей (или уменьшении толщины масляной пленки) внешняя нагрузка Q , действующая на сопряжение, равна алгебраической сумме несущей силы вытесняемой смазки Q _В и несущей гидродинамической силы Q _Г, возникающей вследствие перемещения точки контакта по рабочим поверхностям кулачка и толкателя:

Q = Q _В+ Q _Г. (1)

На основе изложенной методики разработан алгоритм пошагового итерационного расчета нестационарного значения толщины масляной пленки в сопряжении кулачок-толкатель. При этом производная dh/dt в (3) представляется в конечно-разностном виде, а в качестве внешней нагрузки Q может быть использована как квазистатическая сила в приводе, равная сумме сил клапанных пружин и инерции приведенных к толкателю масс движущихся деталей механизма, так и сила, рассчитываемая путем математического моделирования динамики МГР. В последнем случае дополнительно учитываются колебательные процессы в клапанном приводе, и расчет является более точным.

В связи с этим рассмотрим расчет гидродинамики смазки в зазорах МГР в рамках обобщенной математической модели его динамики, позволяющей исследовать клапанные механизмы различных типов с учетом их существенных особенностей, таких как начальные усилия и зазоры в связях, рассеяние энергии при колебаниях, наличие односторонних связей и возможность разрыва кинематической цепи, ударные взаимодействия деталей при восстановлении контактов в звеньях, переменность параметров (передаточных чисел, жесткостей, силы давления газов на тарелку клапана).

Дифференциальные уравнения движения системы из N-связанных масс имеют вид ni m^ P - F +E (Pn — Fn) (i = I-., N),   (2)

n = 1

где m i - величина i-й массы; x i - ее ускорение; P i -внешняя сила, действующая на i -ю массу (например, сила от давления газов в цилиндре); F_i – сила внешнего трения; n_i – общее количество связей i-й массы с другими или с неподвижной заделкой; P_in и F_in – силы соответственно от упругой деформации и внутреннего трения в n -й связи, действующие на i -ю массу.

Сила вязкого трения

F i = b P ,                  ⁽³⁾

где b i - коэффициент внешнего трения; x i - скорость i -й массы.

Для двухсторонней связи, передающей как растягивающие, так и сжимающие усилия,

P = + ^{( P} „ ) o ^- c„ ⁽ X ^- x j / r in ± s in ) ,       (4)

где ( P_in )₀ – начальное усилие (при x_i = x_j = 0 ; c_in – жесткость связи; x_i и x_j – перемещения соответственно i -й и j -й масс; j – номер массы, соответствующей связи n ; r_in – передаточное отношение связи ( r_in не равно единице, например, для коромысла); s_in – кинематическое возбуждение, определяемое законом перемещения толкателя для связи кулачок-толкатель, либо законом перемещения плунжера гидрокомпенсатора при наличии последнего в данной связи. В других случаях величина s_in полагается равной нулю. В (4) и ниже верхний знак соответствует случаю, когда масса j расположена далее массы i в положительном направлении оси OX , а нижний знак – противоположному случаю. ( P_in )₀ положительно для сжатой и отрицательно для растянутой связи.

В односторонней связи (не передающей растягивающие усилия) возможно возникновение зазора δ_in при относительном расхождении масс. Тогда при наличии кинематического возбуждения

^Pin = + ^{( P}in ) 0 — c in ^[ x i — x j / r in ± ⁽ s in ⁺ § in — ^A in ^)] , (5)

где 5_in и A in - соответственно текущее и начальное (при нулевых перемещениях масс) значения зазоров.

Очевидно, при соблюдении условия равновесия хотя бы одно из начальных значений A in и ( P in )₀ должно быть равно нулю, если только в данной связи отсутствует несущая гидродинамическая сила. Величина δ_in при отсутствии смазки в зазоре определяется по формуле:

^S in = maxHA n, ^{- (} P ) о / c ,n ^- s in + ⁽ x . ^- x j / r „ ^)],0} . (6)

Сила внутреннего трения F_in в связи принимается пропорциональной скорости ее деформации. Для двухсторонней связи

F in I x i - x j / r in ± s in ) (7) где b in - коэффициент внутреннего трения; x j -скорость j -й массы, s in - скорость кинематического возбуждения.

Для односторонней связи выражение (7) справедливо при равном нулю зазоре δ _n . В противном случае при отсутствии смазки в зазоре величина F _n полагается равной нулю.

Пусть зазор заполнен маслом, и соответствующая упругая связь сжата, то есть выражение ( P _n – F _n ) меньше нуля, если масса j расположена далее массы i в положительном направлении оси OX , и ( P _in – F _n ) больше нуля в противоположном случае. Тогда при чистом вытеснении смазки для определения δ _n следует вместо (6) использовать, следующее соотношение:

S in =- Pn - Fn ^ n / Kn . (8)

Если же соответствующая односторонняя связь, не передающая растягивающих усилий, не является сжатой (то есть выражение ( P _n – F _n ) принимает нулевое значение), предполагаем, что величина δ _n может увеличиваться в случае взаимного расхождения масс:

^S in = max ^{ [ - Sin + ⁽ x^ i ^- x t j I rin ^)],0} . (9)

Соответственно, сила внутреннего трения в связи рассчитывается по формуле

Fin = bin ^[ xi ^- xj ¹ rin ± ⁽ sin ^{+ S} in ) ] • ⁽¹⁰⁾

Изложенный подход позволяет строить математические модели клапанного привода с учетом гидродинамики смазки в его зазорах, количество и параметры которых задаются в исходных данных. Уравнения (2) после понижения порядка путем введения дополнительных переменных в сочетании с (9) или (10) образуют систему, решаемую методом Рунге-Кутта.

С использованием идентифицированной по экспериментальным данным девятимассовой динамической модели [2] привода выпускного клапана двигателя 8ЧВН15/16 выполнены расчеты чистого вытеснения смазки из теплового зазора, а также определена толщина масляной пленки в сопряжении кулачок-толкатель.

На рисунке 1 приведены графики изменения толщины масляной пленки в тепловом зазоре МГР для двух значений частоты вра-

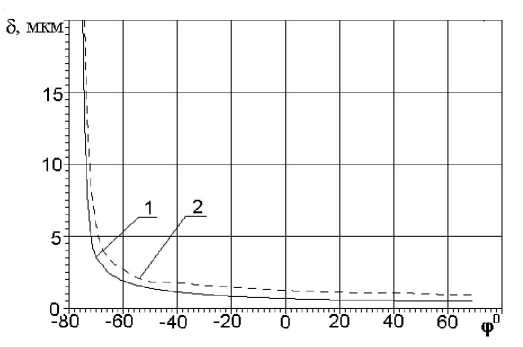
Рис. 1. Толщина масляной пленки в тепловом зазоре МГР двигателя 8ЧВН15/16 в зависимости от угла поворота кулачка (случай чистого вытеснения масла):

1 – n = 600 об/мин; 2 – n = 2000 об/мин

щения коленчатого вала. При этом зазор, начальное значение которого задавалось равным 0,1 мм, вводился в связь между элементами, моделирующими штангу толкателя и коромысло, причем форма контакта принималась круговой с радиусом 5 мм.

Расчет вытеснения смазки из зазора позволяет учесть рассеяние энергии в слое смазки дополнительно к потерям на внешнее и внутреннее трение. При этом также изменяются жесткостные характеристики связи. Так, ее приведенная жесткость, рассчитанная с учетом уменьшения толщины масляной пленки, меньше заданной статической жесткости, и переменна по углу поворота кулачка [1]. Отмеченные обстоятельства оказывают влияние на результаты моделирования динамики клапанного привода. На рисунке 2 при- ведены результаты сравнительных расчетов силы, действующей со стороны коромысла на клапан в начальный период его подъема при исходной величине теплового зазора 0,3 мм и частоте вращения коленчатого вала двигателя 1900 об/мин. Плавность нарастания силы при вступлении механизма в работу, характерная для расчета с учетом вытеснения масла (кривая 2), хорошо согласуется с экспериментальными данными. При этом наблюдается смягчение ударного взаимодействия деталей при восстановлении контактов в звеньях как в начале движения клапана, так и в случае разрывов кинематической цепи.

При наличии масла в зазоре (кривая 2 на рисунке 2) первые максимальное и минимальное пиковые значения силы равны соответственно 1255 Н и 690 Н, в то время как

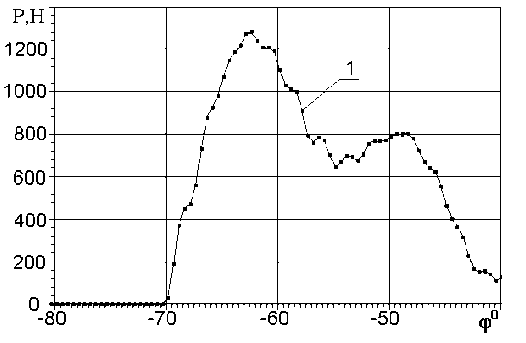
а)

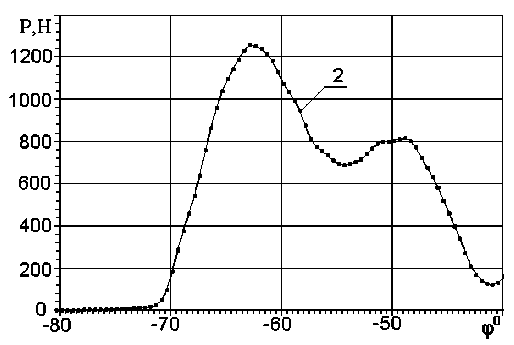
б)

Рис. 2. Сила в коромысле привода клапана двигателя 8ЧВН15/16 в зависимости от угла поворота кулачка: а) без учета гидродинамики смазки; б) с учетом гидродинамики смазки

эти же параметры при расчете без учета вытеснения масла (кривая 1 на рисунке 2) равны 1 281 Н и 643 Н. Различие интенсивности возбуждаемых в приводе высокочастотных колебаний в начальной фазе движения клапана, хорошо заметные при сравнении кривых 1 и 2 на рисунке 2, становятся более существенными при увеличении зазора и частоты вращения распределительного вала. Поскольку высокочастотные колебания быстро затухают, различия в динамике при посадке клапана, вызванные учетом вытеснения масла из зазоров, менее существенны. Таким образом, анализ полученных результатов позволяет сделать вывод о том, что учет наличия масляных пленок между элементами повышает адекватность математической модели динамики МГР.

На рисунке 3 приведены результаты расчета толщины масляной пленки в сопряжении кулачок-толкатель. Кривая 1 получена на основе формулы (4) (квазистационарный расчет) при нагружении сопряжения силами клапанных пружин и инерции приведенных к толкателю движущихся масс. Кривая 2 соответствует расчету с учетом эффекта вытеснения смазки по изложенной выше методике (нестационарный расчет) и таком же, как и для кривой 1, квазистатическом нагружении сопряжения. Наконец, кривая 3 рассчитана с учетом как нестационарности гидродинамики смазки, так и наличия колебательных процессов в механизме, моделируемых на основе представленной выше обобщенной математической модели динамики МГР. Расчет выполнен для частоты вращения коленчатого вала 1700 об/мин и нулевого теплового зазора.

Кривые 1 и 2 различаются вследствие наличия эффекта вытеснения смазки. Отличия особенно заметны в области минимальных толщин и становятся более существенными с ростом частоты вращения кулачка, а также при разрывном ускорении толкателя.

Заметно также влияние на результаты более точного расчета сил с учетом колебательных процессов в механизме. Различия кривых 2 и 3 наибольшие также в зонах действия вытеснительных эффектов и невелики при отсутствии последних. Это объясняется тем, что при использовании (4) изменение нагрузки слабо влияет на h _min вследствие малого показателя степени у Q _Г, равного (–0,13). Увеличение h _min в начале и конце движения клапана для кривой 3 по сравнению с кривыми 1 и 2 вызвано тем, что при математическом моделировании динамики, в отличие от квазистатического расчета силы, обеспечивается постепенность нагрузки и разгрузки сопряжения.

Таким образом, разработанная обобщенная математическая модель динамики МГР, позволяющая рассчитывать гидродинамику смазки в его сопряжениях, обеспечивает более точное определение динамических и трибологических характеристик механизма, являющихся основой для оценки его работоспособности и надежности.

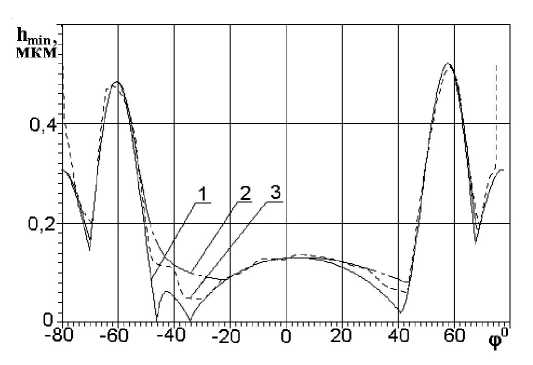
Рис. 3. Минимальная толщина масляной пленки в сопряжении кулачок-толкатель двигателя 8ЧВН15/16 в зависимости от угла поворота кулачка:

1 – квазистатический расчет; 2 – расчет с учетом нестационарности режима смазки;

3 – расчет с учетом нестационарности режима смазки и колебательных процессов в МГР