Исследование графов модифицированной пузырьковой сортировки на основе высокопроизводительных вычислений

Введение. Определение графа Кэли было дано известным английским математиком Артуром Кэли в XIX веке для представления алгебраической группы, заданной фиксированным множеством порождающих элементов.

В последние десятилетия теория графов Кэли развивается как отдельная большая ветвь теории графов. Графы Кэли находят применение как в математике, так и за ее пределами. Эффективное применение графы Кэли нашли в информационных технологиях после пионерской работы 1986 года С. Эйкерса и Б. Кришнамурти [1], которые впервые предложили применять указанные графы для представления компьютерных сетей, в том числе для моделирования топологий многопроцессорных вычислительных систем (МВС) – суперкомпьютеров. С тех пор данное направление активно развивается [2–11]. Это связано с тем, что графы Кэли имеют много привлекательных свойств, из которых стоит отметить их регулярность, вершинную транзитивность, малые диаметр и степень при достаточно большом количестве вершин в графе. Например, такие базовые топологии сети, как «кольцо», «гиперкуб» и «тор», являются графами Кэли.

Напомним определения основных терминов, используемых в работе.

Пусть X – порождающее множество группы G , т. е. G = ( X ). Графом Кэли Г = Cay ( G , X ) = ( V , E ) называют ориентированный граф, обладающий следующими свойствами:

• a)    множество вершин V (Г) соответствуют элементам группы G ;

• б)    множество ребер E (Г) состоит из всех упорядоченных пар ( g , xg ), где g e G и x e X .

В дальнейшем будем считать порождающее множество X симметричным и свободным от единичного элемента группы, т. е. x e X ^ x ^{- 1} e X и e 4 X . Поскольку X является свободным от единичного элемента, то граф Г не содержит петель. Симметричность порождающего множества означает, что граф будет неориентированным и без кратных ребер, т. е. если в графе имеется ребро из g в xg , то оно совпадает с ребром из xg в x ^{- 1} ( xg ) = g .

Таким образом, Г = Cay ( G , X ) = (V , E ), где V = G и E = {{ g , xg } | g e G , x e X }.

Количество вершин | V | равно порядку группы G . Граф Кэли является регулярным, и его степень s , т. е. количество ребер, выходящее из каждой вершины, равно числу порождающих элементов группы: 5 = | X |.

Шаром K_s радиуса s группы G будем называть множество всех ее элементов, которые могут быть представлены в виде групповых слов в алфавите X длиною, не превышающей s . Для каждого целого неотрицательного s можно определить функцию роста группы F ( s ), которая будет равна числу элементов группы G относительно X , представимых в виде несократимых групповых слов длиною s . Таким образом,

F (0) = |K o l = 1, F ( 5 ) = ^HK - 1 1 при 5 e N .

Как правило, функцию роста конечной группы представляют в виде таблицы, в которую записывают ненулевые значения F ( s ).

Отметим также, что при вычислении функции роста группы мы параллельно выясняем характеристики соответствующего графа Кэли, например, такие как диаметр и средний диаметр [12]. Пусть F ( 5 ₀) >  0, но F ( 5 ₀ + 1) = 0, тогда 5 ₀ будет являться диаметром графа Кэли группы G в алфавите порождающих X , который мы будем обозначать D_X ( G ). Соответственно, средний диаметр D_X ( G ) равен средней длине минимальных (несократимых) групповых слов.

Вычисление диаметра графа Кэли большой конечной группы является хотя и разрешимой, но весьма сложной проблемой. Это связано с тем, что в общем случае задача по определению минимального слова в группе, как показали С. Ивен и О. Голдрейх в 1981 году [13], является NP-трудной (nondeterministic polynomial). Таким образом, в наихудшем случае количество элементарных операций, которые необходимо выполнить для решения указанной задачи, представляет собой экспоненциальную функцию от |X|. Поэтому для эффективного решения задач на графах Кэли, имеющих большое количество вершин, необходимо применять МВС.

Пусть Sn = (Xn), где Xn ={(i, i + 1)| i = 1, 2, „., n} - симметрическая группа, порожденная множеством транспозиций Xn. Граф Кэли BSn = Cay(Sn, Xn) называют графом пузырьковой сортировки (bubblesort graph) [5]. Свойства данного графа хорошо известны [5] , в частности,

D X n ( S n ) = n ’ ⁿ 2 ” и D X n ( S n ) =

D X n ( S n )

.

Пусть теперь S n = ( X n j, где X_n = X n u { (1, n ) } .

Граф Кэли MBS _n = Cay ( S_n, X_n ) называют графом модифицированной пузырьковой сортировки (modified bubble-sort graph) [5]. На сегодняшний день известны характеристики данного графа только для n <  13. В работе [14] получено, что

, 2

D X n ( S n ) =Т

и D - ( S_n ) = nn + 1 при n <  13. ^Xn            6

В настоящей работе представлена модифицированная версия алгоритма A–I из [15], на основе которого при помощи суперкомпьютерных вычислений получены ранее неизвестные характеристики MBS n -графов для n = 14 и 15.

Алгоритм A–I

Вход: конечная группа G = ( X , °^, где Х = = { x 1 , x 2 ,..., x m } - порождающее множество G .

Выход: диаметр D_X ( G ), средний диаметр D_X ( G ) графа Кэли Г = Cay ( G , X ), а также функция роста F ( 5 ) группы G , где 0 <  5 <  D_X ( G ).

• 1.    5 = 0, K 0 = { e }, F (0) = 1, P = K 0 .

• 2.    5 = 5 + 1.

• 3.    K = K . 5        5 — 1

• 4.    V x e X и V p e P :

  • 4.1.    g = x ° p ;

  • 4.2.    если g e K 5 , то K 5 = K 5 и { g }.

• 5.    P = K₅ — K_{5 —} 1 .

• 6.    F ( s ) =| P |.

• 7.    Если F ( 5 ) >  0, то переход п. 2; иначе 5 ₀ = 5 — 1, переход п. 8.

• 8.    D_x ( G ) = 5 0 , D x ( G ) = I----г E F ( 5 ) • 5 .

• 9.    Выход.

s 0

I ^K 5 0| 5 = 0

В [15] доказана корректность алгоритма A–I, а также получено, что T ( | G | ) e 0 ( | G |² ) при | X | ^ | G |, где T ( | G | ) - вычислительная сложность алгоритма A-I и 0 - одновременно верхняя и нижняя асимптотическая оценка сложности.

Для снижения вычислительной сложности требуется способ для нумерации элементов [15]. Пусть g = ( а 1 , а ₂, . ^, а _n ) - произвольная перестановка из S n .

Используя факториальную систему счисления можно однозначно определить номер перестановки (при этом нумерация будет начинаться с нуля). Определим биективное отображение ф следующего вида:

n g ^фф^ ng = Ё bkk!

к = 1

Здесь n_g представляет собой целое неотрицательное число, записанное в факториальной системе счисления, при этом коэффициент b_k при множителе k ! будет обозначать число инверсий для элемента а _{к + 1} в том множестве, в котором производятся перестановки (количество элементов, меньших а _{к + 1}, но стоящих правее его в рассматриваемой перестановке). Легко увидеть, что n g пробегает все значения от 0 до n ! - 1.

Модифицируем алгоритм A–I следующим образом. В п. 1 добавим булев вектор V , размерностью n !, все элементы которого первоначально равны 0. Для удобства индексация элементов V начинается с 0. Ввиду того, что K ₀ = {e} и ф ( e ) = 0, запишем V 0 = 1.

Заменим п. 4.2 алгоритма A–I на следующий:

4.2. если V n g = 0 , то V n g = 1 и K s = K s и { g }.

Поскольку сложность процедуры перевода перестановки в число и обратно равна 0 (1), то согласно [15] сложность модифицированного алгоритма A–I будет равна 0 (| G |).

Также отметим, что в п. 4.1 все элементы g вычисляются независимо друг от друга, поэтому этот уча-

сток алгоритма можно легко распараллелить. В этом случае сначала параллельно вычисляются все произведения g , а затем для каждого элемента получившегося массива последовательно выполняется п. 4.2.

Исследование MBS-графов. Модифицированный алгоритм A–I был реализован на языке С++ и апробирован на 96-ядерном сервере суперкомпьютера СФУ, при этом было задействовано 512 Гб оперативной памяти и 8 Тб дискового пространства. В результате были вычислены функции роста групп 5 14 = ^ X u) и 5 15 = ^ X ₁₅^ . Затраченное на расчеты время равно примерно 2,5 часа для n = 14 и 46 часов для n = 15. В табл. 1, 2 приведены функции роста групп S ₁₄ и S ₁₅ , а на рис. 1, 2 – их графики. Из табл. 1, 2 следует, что

D^ ( 5 ₄) = 49 = —, D^ ( 5 ₄) = 30 1 =-------- ,

X 14 14              4 X 14 14         2          6

D^ 5 15 ) = 56 =

^D x ₅ ( ⁵ 15 ) = ³⁵6 =

15 2 - 15 + 1

Таким образом мы можем расширить результат из [14]:

Теорема. Пусть 5_n = ( XЛ и n <  15. Тогда верно,

что

DX, ( 5. ) =

n ²

и DX. (5п) = -

- n +1

.

Таблица 1

Функция роста группы S ₁₄ в алфавите X ^ˆ ₁₄

s	F ( s )	s	F ( s )	s	F ( s )	s	F ( s )	s	F ( s )
0	1	10	1144066	20	523576508	30	7875671024	40	439630193
1	14	11	2496144	21	807898884	31	8184285564	41	177894717
2	105	12	5200300	22	1206399194	32	8059876006	42	59073300
3	560	13	10399573	23	1741769068	33	7486458696	43	15497794
4	2380	14	20044817	24	2428791549	34	6521589932	44	3095274
5	8568	15	37346764	25	3266926299	35	5291298298	45	457459
6	27132	16	67385500	26	4232447674	36	3964966720	46	46501
7	77520	17	117857285	27	5272211438	37	2715665810	47	2912
8	203490	18	199872075	28	6301765938	38	1678335828	48	93
9	497420	19	328616470	29	7210522410	39	920955932	49	1
| S 14 |=14!=87178291200

Таблица 2

Функция роста группы S ₁₅ в алфавите X ^ˆ ₁₅

s	F ( s )	s	F ( s )	s	F ( s )	s	F ( s )	s	F ( s )
0	1	12	9657700	24	8330511890	36	111514773216	48	723446997
1	15	13	20058300	25	12267072742	37	108665304904	49	217500207
2	120	14	40115312	26	17570631028	38	100844738930	50	52359036

Окончание табл. 2

s	F ( s )	s	F ( s )	s	F ( s )	s	F ( s )	s	F ( s )
3	680	15	77540544	27	24463138336	39	88757487936	51	9748102
4	3060	16	145284325	28	33079985068	40	73721997284	52	1343342
5	11628	17	264439921	29	43405123242	41	57447140400	53	126700
6	38760	18	468283120	30	55204143800	42	41700857614	54	7282
7	116280	19	807550010	31	67970322498	43	27958028594	55	210
8	319770	20	1356808058	32	80902850743	44	17132134736	56	2
9	817190	21	2221351570	33	92936928305	45	9472716396
10	1961256	22	3543440716	34	102839910030	46	4651580804
11	4457400	23	5505931806	35	109374995290	47	1989274794
| S 15 |=15!=1307674368000

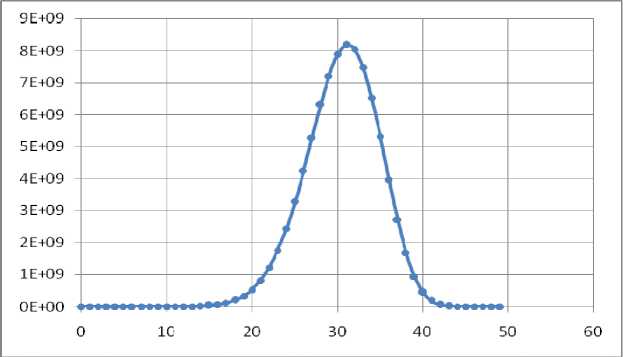
Рис. 1. График функции роста группы S ₁₄

• Fig. 1.    Graph of group growth function

  

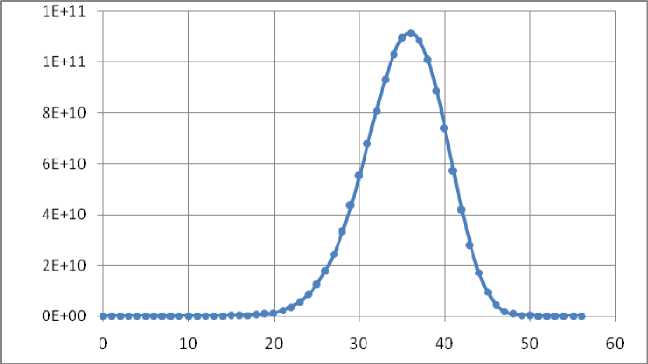
  Рис. 2. График функции роста группы S ₁₅

  
  

• Fig. 2.    Graph of group growth function

Заключение. Применение высокопроизводительных вычислений позволило продвинуться в изучении свойств MBS n -графов. Несмотря на это, представить аналитическое решение для произвольного n на сегодняшний день не представляется возможным.

Acknowledgments. The reported study was funded by RFBR and the government of Krasnoyarsk region according to the research project № 17-47-240318.