Исследование граничных значений задержек трафика VPN с учетом конкурирующих потоков
Автор: Лысиков Андрей Александрович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии компьютерных систем и сетей
Статья в выпуске: 1 т.15, 2017 года.
Бесплатный доступ
В статье рассматривается задача оптимального распределения ресурсов в сети оператора связи при реализации множества виртуальных частных сетей VPN. Предлагается модель виртуальной частной сети на основе теории сетевого исчисления, позволяющая определять наименьшую верхнюю границу сквозной задержки передачи пакетов потока планируемой VPN с учетом трафика конкурирующих потоков других VPN, проходящих через последовательность сетевых узлов рассматриваемой виртуальной сети. Представлены результаты экспериментального исследования предложенной модели. Даны рекомендации операторам связи по использованию полученных результатов на практике при планировании распределения сетевых ресурсов. Предложенная модель может стать основой для разработки специализированного программного пакета планирования услуг VPN, который позволит операторам связи эффективно использовать имеющиеся сетевые ресурсы и обеспечить гарантированное качество обслуживания.
Виртуальные частные сети, оптимальное распределение ресурсов сети оператора связи, граничные значения задержек, теория сетевого исчисления
Короткий адрес: https://sciup.org/140191863
IDR: 140191863 | УДК: 621.391. | DOI: 10.18469/ikt.2017.15.1.06
Текст научной статьи Исследование граничных значений задержек трафика VPN с учетом конкурирующих потоков
В настоящее время активно развивается концепция программно-конфигурируемых сетей SDN (Software-Defined Network) c использованием сетевой виртуализации NFV (Network Functions Virtualization), предлагаемая как следующий этап эволюции существующей концепции построения сетей NGN (Next Generation Networks) и 4G. Прототипом виртуализации послужили виртуальные частные сети VPN (Virtual Private Network), являющиеся одной из наиболее востребованных услуг в сетях NGN [1].
Сеть VPN представляет собой набор фиксированных маршрутов, проходящих через определенные сетевые узлы. Как правило, в сети оператора связи одновременно реализуется множество таких виртуальных сетей. Для каждой VPN оператором должны строго соблюдаться установленные в соглашении о гарантированном уровне сервиса SLA (Service Level Agree-ment) характеристики качества обслуживания QoS (Quality of Service) (например, задержка передачи пакетов, гарантированная полоса пропускания, доля потерянных пакетов и др.).
В местах пересечения большого числа потоков трафика различных VPN возникают конфликты при совместном использовании ресурсов узлов и каналов связи. Поэтому при вводе каждой новой VPN оператору необходимо распределить ресурсы своей сети так, чтобы, с одной стороны, предоставить услугу VPN максимальному количеству клиентов с гарантированным QoS, а с дру- гой стороны, обеспечить эффективное использование ресурсов узлов и каналов связи. Иными словами, оператор на этапе планирования новой VPN должен определить для нее один или несколько оптимальных сетевых маршрутов.
По аналогии с алгоритмами маршрутизации в IP-сетях, оптимальный маршрут для VPN можно определить на основе различных метрик, например его длины или сквозных характеристик QoS. Первый подход является достаточно простым и подразумевает выбор кратчайшего маршрута в сети как наиболее оптимального. Однако в этом случае возникает риск неэффективного использования сетевых ресурсов, так как при перегрузке такого маршрута пакеты трафика все равно будут передаваться по нему, создавая большие очереди в буферах узлов, в то время как трафик можно было бы направить по более длинному, но менее загруженному маршруту. В таком случае второй подход выглядит более выгодным, если в качестве критерия выбора оптимального маршрута, например, использовать значение сквозной задержки.
Классическими для анализа характеристик QoS в мультисервисных сетях связи являются модели на основе теории массового обслуживания (ТМО). При моделировании современных пакетных сетей данные модели имеют ограничения. Основным ограничением ТМО при анализе последовательно соединенных узлов является предположение о том, что потоки пакетов и дисциплины их обслуживания в узлах сети чаще все- го описываются марковскими процессами, что позволяет анализировать пакетные сети для простейших моделей трафика и дисциплин обслуживания. К тому же большое количество исследований показывает, что трафик в мультисервисных сетях имеет гораздо более сложный характер, например проявляет свойства самоподобия.
Модели на основе ТМО позволяют определять средние значения характеристик QoS, что является еще одним существенным ограничением. При расчете средних значений происходит недооценка возможных пиковых значений характеристик QoS. В то же время, ведущая международная организация по стандартизации в области телекоммуникаций – сектор стандартизации телекоммуникаций Международного союза электросвязи (МСЭ-Т) в своих рекомендациях регламентирует граничные значения QoS в мультисервисных сетях на основе протокола IP. Например, в Рекомендации G.1010 указано, что задержка при двухсторонней голосовой связи в норме не должна превышать 150 мс, а максимальная задержка должна быть меньше 400 мс.
Указанные недостатки ТМО преодолены в теории сетевого исчисления NC (Network Calculus) [2], которая позволяет определять граничные значения характеристик QoS пакетных сетей с использованием моделей потоков трафика и сетевых узлов, максимально близких к реальным.
Основы теории сетевого исчисления
Математический аппарат теории NC основан на идемпотентных (max,+) и (min,+) алгебрах [3-4]. В идемпотентной алгебре базовые операции классической алгебры заменяются на их идемпотентные аналоги: умножение становится сложением, а сложение становится операцией нахождения максимума или минимума. Например, в (min,+) -алгебре эти операции представляются, как:
a • b: = a + b , a + b:- min[a,A].
(max,+) -алгеброй называют полукольцо Rmax.+ =(Rury4max,+). (min,+)-алгеброй называют полукольцо Rmm,. =(Roj+^},min.+).
Важными операциями в идемпотентной алгебре являются свертка и обратная свертка функций. Например, в (min,+) -алгебре свертку и обратную свертку двух произвольных функций 7(0 и g(s) можно представить, соответственно, как:
(/®gX4= inf W-^+gO)},
(/ ^X^supl/'O+'O-gO)}, X>0
где inf обозначает точную нижнюю грань функций /(0 и g(s) , а sup – точную верхнюю грань этих функций. Математический аппарат идемпотентных алгебр, лежащий в основе NC, позволяет нелинейные задачи классической алгебры сводить к линейным над соответствующими идемпотентными полукольцами.
Ж0

>D^
Рис. 1. Модель узла сети в теории NC
Модель сетевого узла в терминах NC представлена на рис. 1. Пусть входящий в узел поток трафика характеризуется кумулятивной функцией поступления пакетов X(f) . Поток обслуженных пакетов на выходе узла характеризуется кумулятивной функцией ^^co . Основная идея теории NC состоит в том, что граничные значения характеристик QoS можно получить путем определения максимального горизонтального и вертикального расстояния между кривыми функций ^(^) и D(t) . В частности, граница задержки d в любой момент времени t определяется как максимальное горизонтальное расстояние между ^0) и D(t) , что можно представить, как:
d(A,D,t):=inf deR+,D(f+d)>^(t) , где R – множество неотрицательных чисел. Граничное значение загрузки (числа пакетов в системе) b в любой момент времени t определяется как максимальное вертикальное расстояние между кривыми A(f) и D^ , что можно представить, как:
b^A,D,ty= A(0-D(0.
Для всего потока пакетов граничные значения задержки и загрузки определяются, соответственно, как:
d^A,Dy=sup inf deR+, D(t+d)>A(f)
t>0
b^A,Dy = sup (/4(7) - D(t)) t > 0
Для вычисления граничных значений характеристик QoS необходимо задать законы распределения, описывающие поступающий поток пакетов и дисци- плину его обслуживания в узле. Для этого в NC используются кривая поступления aU), описывающая входящий в узел поток трафика, и кривая обслуживания P^ , описывающая дисциплину обслуживания этого потока в узле . Функция a(t) будет являться кривой поступления для потока трафика на входе узла при условии, что для некоторого наблюдаемого периода времени [O,/] выполняется следующее неравенство:
A(t)-A(s) < att-sY Q
Функция P^ является кривой обслуживания для узла сети при условии, что для некоторого наблюдаемого периода времени [o, /]:
DUA > inf [Л(/-5) + /?(5)], 0
где ° – символ свертки.
Таким образом, граничные значения задержки пакетов потока трафика и загрузки узла будут определяться, соответственно, как максимальные горизонтальное и вертикальное расстояния между кривыми a(/) и P(/) .
В цепочке последовательно соединенных узлов поток на выходе одного узла является входящим потоком в следующий узел и определяется путем (min,+) -свертки кривой входящего потока с кривой обслуживания узла. Благодаря этому NC позволяет последовательность из N узлов анализировать как один узел (см. рис. 2) путем свертки кривых обслуживания узлов, входящих в эту последовательно сть:
P (0 = Pl(0®P7(0<3>...<8>PA f?).
Таким образом, зная кривую поступления трафика в первый узел и кривые обслуживания каждого узла, можно определить сквозные характеристики QoS для потоков, проходящих через такую последовательность узлов.
am
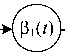
dm=a2w
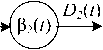
An-M-DnM) PPTP ■ —-—hP,v(O
D,M
—►

Рис. 2. Свертка последовательности сетевых узлов в один узел
Для определения граничных значений задержки основного потока при прохождении через узел конкурирующего потока (см. рис. 3) необходимо определить остаточную кривую обслуживания узла. Для этого случая в [5] была доказана следующая теорема.
Теорема 1. Пусть узел без потерь обслуживает основной и конкурирующий потоки в порядке FIFO. Предположим, что пакеты поступают мгновенно и узел гарантирует минимальную кривую обслуживания P(0 для суммы двух потоков. Пусть конкурирующий поток характеризуется кривой поступления a^(t) . Определим семейство кривых обслуживания для основного потока:
Р^Лт) = [p(?)-a2a-r)p -1^ > ^ •
Если для любого t>0 функция Pi^T) является в широком смысле возрастающей, то узел будет обслуживать основной поток c остаточной кривой обслуживания Р](Лт). Выражение [■^ ] обозначает max{0,x}; множитель
ной функцией.
XM>^
является индикатор-

a,(Z)
Рис. 3. Узел сети с основным И](?) и конкурирующим ^2(0 потоками
Кривая поступления и кривая обслуживания могут быть заданы детерминированными или вероятностными функциями, поэтому NC получила развитие по детерминистическому [5] и стохастическому [6] направлениям.
Модель VPN на основе теории сетевого исчисления
В основу модели VPN положена методология LUDB (Least Upper Delay Bound) [7], которая использует математический аппарат детерминисти- ческой теории NC и позволяет определять наименьшую верхнюю границу задержки для потока трафика, проходящего через последовательность сетевых узлов с учетом конкурирующих потоков.
Рассмотрим модель узла сети c основным потоком VPN и одним конкурирующим потоком, подобную представленной на рис. 3. Кривую поступления основного потока ^i (О и кривую поступления конкурирующего потока а2 (О зададим функциями вида :
ной кривой обслуживания узла при обслуживании основного потока и определяться как
Е(л,а,8) = 8^ ®
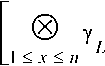
где символ ® обозначает (min,+) -свертку, s – свободный параметр; л=8^ ®
1<х<л сл-’р
K=h(a,n)+s ; £=р _{5+/г(а,л)-Л}-(су-с1 _),р -р;
а(0=ад.+рд-7,
где о - максимальный всплеск потока, р -постоянная скорость потока при условии, что t > 0 , 1 < х < и , где n – общее число потоков, входящих в узел. Кривую обслуживания узла Р(?) зададим функцией вида :
/1(а,л)=/)+ max
(3-0
Р
+s;
р*= min (р );
х=1,...,л
+ оо t > ф, ф - D :
8 =8
D (р [0 t < ф, ф = D.
3(0=я-М+,
где R – постоянная скорость обслуживания узла, о – фиксированная задержка обработки пакета в узле при условии, что R > 0 и 6 > О . Графическое изображение данных кривых поступления и обслуживания показано на рис. 4.
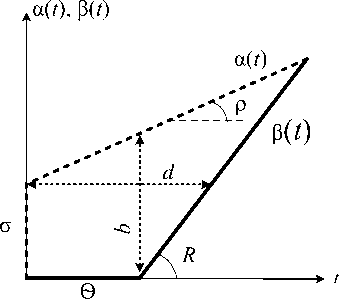
Рис. 4. Кривая поступления (о,р) и кривая обслуживания (9,7?)
Остаточную кривую обслуживания узла определим, используя следствие из теоремы 1, доказанное в [8].
Следствие 1. Пусть л будет псевдоаффинной кривой, смещенной по оси x на расстояние D и состоящей из n сегментов Y при 1 < х < и.
Пусть а = у при Р ^Р. Л- Л-а,р л
Если узел характеризуется минимальной кривой обслуживания л для агрегата основного и конкурирующего потоков, который обслуживается в порядке FIFO, а конкурирующий поток характеризуется кривой поступления а , то семейство функций {Е(л,а,5),5 > о} будет являться остаточ-
На рис. 5 изображена остаточная кривая обслуживания сетевого узла при обслуживании основного потока VPN с учетом одного конкурирующего потока.
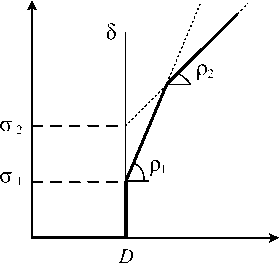
Рис. 5. Остаточная кривая обслуживания узла при обслуживании основного потока VPN c учетом одного конкурирующего потока
Таким образом, граница задержки основного потока VPN в сетевом узле с n конкурирующими потоками определяется как
"1 + d=h(a,л)=^+ max ---— .
1<Л<77 Рх
Рассмотрим модель последовательности узлов VPN. Пусть все потоки, проходящие через эту последовательность, характеризуются кривыми поступления вида (2), а все узлы характеризуются кривыми обслуживания вида (3). Каждый поток будем обозначать как (^j) при условии, что 1 < i < j < N , где i обозначает узел входа потока, j – узел выхода потока, N – общее количество узлов в последовательности.
Если пути конкурирующих потоков не пересекаются и (или) вложены друг в друга, то такие потоки будем называть вложенными, а соответствующую последовательность узлов будем называть вложенной. Пример вложенной последовательности узлов изображен на рис. 6а.
2. Произведем преобразование узла 2 и 3 в один узел 2-3 путем свертки кривой обслуживания узла 2 и остаточной кривой обслуживания узла 3, через которые проходит поток :
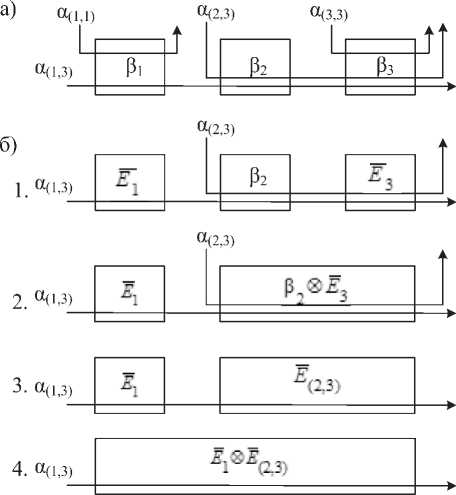
Рис. 6 а) вложенная последовательность узлов VPN; б) алгоритм определения остаточной кривой обслуживания вложенной последовательности узлов
Рг®^^,«(3^3),5(з,з)^
-
3. Используя (3), вычислим остаточную кривую обслуживания узла 2-3, исключив при этом
-
4. Произведем преобразование узлов 1 и 2-3 в один узел 1-2-3 и определим его остаточную кривую обслуживания:
поток
^(2,3) ^^2 ®'Е^3 ’“(3,3) ’^(3,3) Ja(2,3) ,5(2,3)
^(1,2,3) ^^’“(Ц)’1^!,!))®
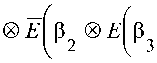
’а(з,з)’^(з,з)
a(2,3)’S(2,3)
Граничное значение сквозной задержки для основного потока VPN, проходящего через последовательность из N узлов, будет определяться как:
В противном случае потоки и последовательности узлов будем называть невложенными. Пример невложенной последовательности узлов изображен на рис. 7 а . Каждый поток во вложенной последовательности будем характеризовать уровнем вложенности, то есть количеством конкурирующих потоков, в которые он вложен. Предположим, что в каждом узле последовательности из N узлов при \ < h < N сумма скоростей всех потоков не превышает скорости обслуживания узла:
d = min< D + max
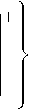
Выражение (6) является задачей кусочно-линейной оптимизации, решение которой подробно рассматривается в [9].
Рассмотрим алгоритм вычисления остаточной кривой обслуживания для вложенной последовательности узлов на примере последовательности, изображенной на рис. 6б.
1. Используя (4), определим остаточные кривые обслуживания в узлах 1 и 3, через которые проходят конкурирующие потоки, имеющие наибольший уровень вложенности (это потоки с кривыми поступления и ):
где свободные параметры, введенные при исключении потоков .
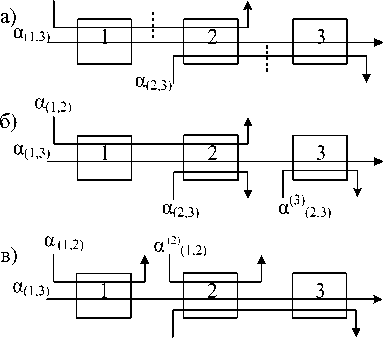
Рис. 7 а ) невложенная последовательность узлов VPN; б-в ) вложенные последовательности узлов
VPN, полученные путем разрезания невложенных конкурирующих потоков
Для определения граничного значения сквозной задержки основного потока VPN в невложенной последовательности узлов, изображенной на рис. 7а, воспользуемся методом, разработанным в [7]:
– из невложенной последовательности узлов получим вложенную путем разрезания конкурирующих потоков VFN a(L2) и a(23);
– определим границу сквозной задержки ^'(1,3) основного потока VPN для последовательности узлов, полученной в результате разрезания потока ^(2 3) , – см. рис. 7 б . Для этого воспользуемся алгоритмом, разработанным в [7]:
-
а) определим общую кривую поступления потоков a(l,2) и a(l,3) в узле 2, которая равна общей кривой потока на выходе узла 1. Используя (1), получим
{(1,2), (2,3)}
a1 + a1 (1,2) (1,3)
-
б) используя (4), определим остаточную кривую обслуживания потока :
(2,3)
2,a2
{(1,2),(2,3)}
-
в) определим кривую поступления потока a , которая равна кривой потока a на выходе узла 2. Используя (1), имеем:
(3) a
(2,3)
(2,3)
Для невложенных последовательностей, состоящих из большого числа узлов с большим количеством потоков, может быть большое множество мест разрезов. Определение оптимального числа мест разрезов для невложенных последовательностей узлов подробно рассмотрено в [8].
Результаты экспериментов
Экспериментальное исследование модели VPN проводилось для вложенной последовательности узлов, представленной на рис. 8, и невложенной последовательности узлов, представленной на рис. 7 а . Для проведения экспериментов использовалась программа DEBORAH [10], основанная на методологии LUDB.
0(2,3) 0(1,1)

Рис. 8. Вложенная последовательность узлов
Целью экспериментального исследования являлась оценка степени влияния конкурирующих потоков на границу задержки d основного потока VPN при различных значениях параметров (m P) кривых поступления потоков и параметров (0,7?) кривых обслуживания узлов.
На рис. 9 представлена зависимость границы задержки d основного потока VPN от доли конкурирующих потоков при увеличении их всплесков во вложенной последовательности узлов (см. рис. 8).
-
г) определим границу сквозной задержки <Л1,3) , используя метод вычисления границы задержки для вложенной последовательности узлов VPN, рассмотренный выше;
– определим границу сквозной задержки ^2d,3) основного потока VPN для последовательности узлов, полученной в результате разрезания потока a^ 3) (рис. 7 в ). Алгоритм аналогичен определению ^'(1,3) ;
– определим границу сквозной задержки основного потока VPN в невложенной последовательности узлов: 6? ) = min ^\l,3), ^2(1,3)).
Таким образом, граница задержки для невложенной последовательности из N узлов VPN будет определяться как
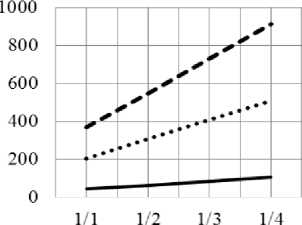
Доля основного потока VPN/ доля конкурирующих потоков \TN
— ОД R......0,5 R---0,9 R
Рис. 9. Зависимость границы задержки основного потока VPN от доли конкурирующих потоков при увеличении размера их всплесков
^(l.W)
=min d (1,7V)
j n
;d (1,7V)
В данном эксперименте постоянная скорость обслуживания каждого узла R принималась равной 10 Мбит/с, задержка каждого узла 9 = 1 мс, скорость основного потока VPN р1 =200 Кбит/с, скорости
конкурирующих потоков Рэ - Р3 = 100Кбит/с с учетом ограничения (5). Величина максимального всплеска трафика °1 основного потока VPN и ^2 ? ^ конкурирующих потоков рассчитывались как о,+оэ+о3=0Д Л , О! +оэ +о3=0,5 R и о]+о?+ст3-0,9Л, что соответствует малой, средней и большой загрузкам узлов. Затем для каждого варианта загрузки узлов всплески потоков задавались в пропорции О1/(О2+О3) соответственно соотношению долей основного и конкурирующих потоков VPN как 1/1, 1/2, 1/3 и 1/4. В таблице 1 приведены значения максимальных всплесков потоков при загрузке узлов ОДЛ , которые использовались при проведении эксперимента.
Таблица 1. Значения максимальных всплесков потоков при загрузке узлов ОДЛ
|
Доли основного потока VPN / Доля конкурирующих потоков |
Кбит |
°2, Кбит |
°3 , Кбит |
|
1/1 |
200 |
100 |
100 |
|
1/2 |
200 |
200 |
200 |
|
1/3 |
200 |
300 |
300 |
|
1/4 |
200 |
400 |
400 |
По результатам эксперимента установлено, что задержка основного потока VPN линейно возрастает при линейном росте параметра максимального всплеска конкурирующих потоков. При различной загрузке узлов увеличение размера всплесков конкурирующих потоков VPN в два, три и четыре раза приводит к увеличению границы задержки d основного потока VPN, соответственно, на 50%, 100% и 150%. При фиксированных равных загрузках узлов и фиксированной доле конкурирующих потоков (например ОДЛ и 1/1) увеличение размера всплесков конкурирующих потоков ведет к пропорциональному увеличению границы задержки d основного потока VPN.
В эксперименте по исследованию зависимости границы задержки d основного потока VPN от доли конкурирующих потоков при увеличении скорости р во вложенной последовательности узлов (см. рис. 8) всплески потоков задавались как о = 100 Кбит и о = о = 50 Кбит. Скорости
1 2 3 z г основного и конкурирующих потоков (соответственно Р,,Р2ир) задавались аналогично параметрам всплесков в предыдущем эксперименте, но с учетом ограничения (5). Скорости и задержки узлов задавались такими же, как и в предыдущем эксперименте.
По результатам эксперимента установлено, что зависимость границы задержки d основного потока VPN от доли конкурирующих потоков при увеличении их скорости р аналогична зависимости, представленной на рис. 9. Однако при различной загрузке узлов увеличение скорости конкурирующих потоков приводит к незначительному увеличению задержки d основного потока VPN. При загрузке каждого узла ОДЛ увеличение скорости конкурирующих потоков в 2, 3 и 4 раза приводит к увеличению границы задержки d основного потока VPN, соответственно, лишь на 1%, 2% и 4%; при загрузке 0,5 Л – на 5,5%, 11% и 17%; при загрузке 0,9 Л – на 10%, 20% и 31%. При фиксированных загрузках узлов и доле конкурирующих потоков увеличение скорости конкурирующих потоков ведет к незначительному увеличению границы задержки d основного потока VPN. Например, при загрузках узлов ОДЛ и доле конкурирующих потоков 1/4 увеличение скорости конкурирующих потоков на 10…20% приводит к увеличению границы задержки d основного потока на 0,4…0,9%, а при загрузке узлов 0,9 Л и доле 1/4 граница задержки возрастает на 3,5 – 7%.
На рис. 10 представлена зависимость границы задержки d основного потока VPN от задержки узлов 0 вложенной последовательности (см. рис. 8) при доле основного и конкурирующих потоков 1/1.
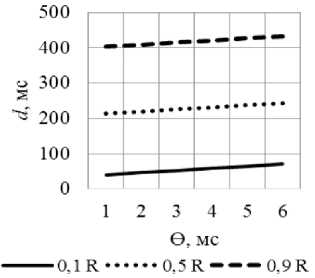
Рис. 10. Зависимость границы задержки основного потока VPN от задержки узла 9 при доле основного и конкурирующих потоков 1/1
В данном эксперименте постоянная скорость обслуживания каждого узла R принималась равной 10 Мбит/с, скорости р с учетом ограничения (5) и всплески о основного и конкурирующих потоков VPN задавались в зависимости от загрузки узлов и соотношения их долей аналогично предыдущим экспериментам.
По результатам эксперимента установлено, что при различной загрузке узлов и различных долях конкурирующих потоков зависимость границы задержки d основного потока от задержки узла 0 является линейной, граница задержки d увеличивается пропорционально увеличению задержки узлов о.
На рис. 11 представлена зависимость границы задержки d основного потока VPN от скорости узлов R во вложенной последовательности (см. рис. 8) при доле основного и конкурирующих потоков 1/1. Скорости р (с учетом ограничения (5)) и всплески основного и конкурирующих потоков задавались в зависимости от загрузки узлов и соотношения их долей аналогично предыдущим экспериментам. По результатам эксперимента установлено, что граница задержки d основного потока VPN убывает нелинейно при увеличении скорости узлов.
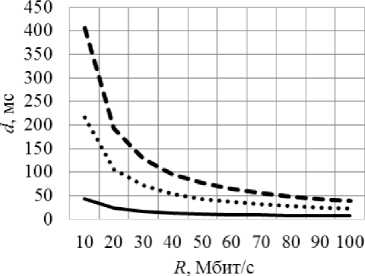
----0.1 R ......0,5 R ---0,9R
Рис. 11. Зависимость границы задержки d основного потока VPN от скорости узлов R во вложенной последовательности при доле основного и конкурирующих потоков 1/1
Экспериментальное исследование невложенной последовательности узлов проводилось с использованием тех же входных данных, что и для вложенной последовательности узлов. Результаты экспериментов аналогичны. Это можно объяснить тем, что граница задержки d основного потока VPN вычислялась для двух вложенных последовательностей, полученных путем разрезания невложенных конкурирующих потоков VPN.
Выводы
Результаты проведенного экспериментального исследования модели VPN позволяют сформулировать следующие выводы.
-
1. Значительное влияние на границу задержки планируемого потока VPN будет оказывать размер максимального всплеска конкурирующих потоков и/или уровня вложенности конкурирующих
-
2. Если все доступные маршруты в сети будут иметь большое число конкурирующих потоков с большими размерами всплесков, то в этом случае для удовлетворения требований границ задержек дополнительных потоков трафика других VPN в случае больших всплесков необходимо повысить скорость обслуживания трафика в узлах.
-
3. Скорость поступления конкурирующих потоков оказывает незначительное влияние на задержку трафика планируемой VPN при небольших загрузках узлов. Однако при больших загрузках наиболее оптимальным будет маршрут, в котором конкурирующие потоки имеют наименьшие скорости поступления пакетов трафика. При этом всегда должно соблюдаться ограничение (5).
-
4. Технологическая задержка обработки пакетов в сетевом узле (без учета ожидания пакетов в буферах) зависит от скорости работы соответствующего программного обеспечения этого узла. Однако в современных узлах связи технологическая задержка обработки пакетов в узлах является очень малой величиной, которая практически не влияет на общую задержку передачи трафика через узел.
потоков. Поэтому если планируемый поток VPN имеет большие всплески трафика, то из нескольких маршрутов более оптимальным для данного потока будет маршрут с меньшим числом конкурирующих потоков и (или) меньшими размерами их максимальных всплесков.
Заключение
В статье предложена модель VPN на основе теории сетевого исчисления, позволяющая определять наименьшую верхнюю границу задержки потока планируемой VPN с учетом конкурирующих потоков на отдельных маршрутах, состоящих из последовательно соединенных узлов. На основе анализа результатов проведенного экспериментального исследования модели VPN установлено, что наибольшее влияние на границу задержки планируемой VPN будут оказывать всплески и уровень вложенности конкурирующих потоков трафика при средних и высоких загрузках сетевых узлов. Скорости конкурирующих потоков будут оказывать заметное влияние на границу задержки потока планируемой VPN при высоких загрузках узлов и большого уровня вложенности конкурирующих потоков на анализируемых маршрутах.
Полученные в результате проведенных экспериментов выводы могут быть использованы операторами связи на практике при планировании услуг VPN. Предложенная модель VPN может быть использована при разработке специализированного программного пакета планирования услуг VPN, который позволит операторам связи эффективно использовать имеющиеся сетевые ресурсы и обеспечить гарантированное качество обслуживания. Исследование выполняется при финансовой поддержке РФФИ в рамках научного проекта № 16-37-00363 мол_а.
Список литературы Исследование граничных значений задержек трафика VPN с учетом конкурирующих потоков
- Росляков А.В. Виртуальные частные сети. Основы построения и применения. М.: Эко-Трендз, 2006. -304 с.
- Cruz R. L. A calculus for network delay. Part I, II. IEEE Transactions on Information Theory, 1991. V. 37(1). -Р. 114-141.
- Литвинов Г.Л. Деквантование Маслова, идемпотентная и тропическая математика: краткое введение//Теория представлений, динамические системы, комбинаторные и алгоритмические методы, XIII. Записки научных семинаров ПОМИ. Т. 326, 2005. -С.145-182.
- Baccelli, F. Cohen, G. Olsder, G.J. Quadrat, J.P. Synchronization and Linearity: An algebra for discrete event systems. John Wiley & Sons Ltd, 1992. -485 p.
- Le Boudec J.-Y., Thiran P. Network Calculus: A Theory of Deterministic Queuing Systems for the Internet. Springer-Verlag, 2012. -263 p.
- Jiang, Y., Yong L. Stochastic Network Calculus. Springer-Verlag, 2008. -240 p.
- Lenzini L., Mingozzi E., Stea G. A Methodology for Computing End-to-end Delay Bounds in FIFO-multiplexing Tandems. Elsevier Performance Evaluation, 2008. V. 65. PP. 922-943.
- Lenzini L., Martorini L., Mingozzi Е., Stea G. Tight End-to-end Per-flow Delay Bounds in FIFO Multiplexing Sink-tree Networks. Performance Evaluation, V. 63, 2006, PP. 956-987.
- Bisti L., Lenzini L., Mingozzi E., Stea G. Numerical analysis of worst-case and-to-end delay bounds in FIFO tandem networks. Real-Time Systems, V. 48, I. 5, 2012, PP. 527-569.
- Website of the Computer Networking Group at the University of Pisa//URL: http://cng1.iet.unipi.it/wiki/index.php/Deborah, continuously updated (д.о. 15.12.2016).


