Исследование характера процесса разрушения ортотропных пластин с концентраторами напряжений на базе вычислительного эксперимента

Закритическая стадия деформирования является одной из характерных особенностей нелинейного поведения материалов, связанного с накоплением структурных повреждений. Вопросы изучения закономерностей закритического деформирования привлекают внимание исследователей в связи с необходимостью использования деформационных резервов материалов для повышения живучести и несущей способности конструкций [1, 2]. Для развития методов расчета ответственных сооружений и конструкций, включающих, в частности, оценку живучести, необходимо получение большого объема данных о характере поведения материалов на закритической стадии деформирования [3, 4]. В частности, для случая перфорированных пластин данные вопросы рассматривались в работе [5].

Одним из инструментов получения данных о закономерностях процессов неупругого деформирования и разрушения является вычислительный эксперимент [6-8]. Так, с помощью вычислительного эксперимента была показана многостадийность процесса накопления повреждений, установлена зависимость ниспадающей ветви диаграммы деформирования от вида напряженного состояния [9, 10].

Для исследования процесса накопления повреждений в нагруженной ортотропной пластине в данной работе используется подход, в соответствии с которым материал заменяется совокупностью структурных элементов с одинаковыми или различными прочностными характеристиками, а процесс накопления повреждений сводится к последовательному изменению жесткостных свойств этих элементов. В данной постановке при определении состояния того или иного структурного элемента в расчет принимаются напряжения, усредненные по элементу.

Вычисление полей напряжений О у ( r ) и деформаций B y ( r ) осуществляется с помощью замкнутой системы уравнений, в которую входят уравнения равновесия, записанные без учета массовых сил, геометрические соотношения Коши и определяющие соотношения, предусматривающие скачкообразное изменение свойств при разрушении по тому или иному механизму. Для ортотропных материалов в плоском напряженном состоянии определяющие соотношения принимают вид

_     1

£и “^Д ТД"а11 Е1(1 -^1)

212(1-^4)

E 1 ( 1 А) ²²,

_     1          Ц2 (1 -X4)

" £ 1 ( 1 -1 ₂ )^П      E ( 1 -X i ) ⁰¹¹

8i i —         ,           х Ti 1,

¹¹ G 12 ( 1 -1 3 ) ¹¹

где E 1 , E ₂, г ₁₂, G ₁₂ - упругие характеристики ортотропного материала, X „ - функции поврежденности, которые в случае хрупкого разрушения могут принимать значения 0 или 1 в зависимости от типа разрушения материала. Воспользуемся моделью разрушения материала по совокупности критериев, которая позволяет различать механизмы разрушения [1]. Для случая ортотропного материала в плоском напряженном состоянии учитываются три различных вида разрушения (отрывы в направлении двух осей ортотропии и сдвиг). Рассмотренные критерии разрушения представляются в виде неравенств, сведенных в таблицу. Здесь x 1 и x ₂ - направления осей ортотропии материала, 8 j^cr -прочностные константы материала.

Совокупность критериев разрушения и схема изменения характеристик ортотропной среды в плоском напряженном состоянии

№ п/п	Механизм разрушения материала	Критерий разрушения	Поврежденность
			X1	X2	X3	X 4
1	Отрыв при растяжении в направлении x 1	cr 8 11 >  ^ 11	1	0	1	1
2	Отрыв при растяжении в направлении x 2	cr 8 22 > 8 22	0	1	1	1
3	Сдвиг в плоскости X 1 Х 2	812 > 812 cr	1	1	1	1
4	Отрыв при растяжении в направлении х 1 после отрыва в направлении x 2	X2 = 1; 811 >  811 cr	1	1	1	1
5	Отрыв при растяжении в направлении x 2 после отрыва в направлении x 1	X 1 = 1; 8 22 > 8 22 cr	1	1	1	1

Алгоритм описания процесса деформирования и разрушения с использованием вышеизложенной математической модели включает в себя на первом этапе построение конечно-элементной модели расчетной области, приложение начальных граничных условий в перемещениях и расчет напряженно-деформированного состояния пластины. Причем устанавливаемая на данном этапе величина перемещений выбирается настолько малой, чтобы под ее действием заведомо не произошло разрушения ни одного элемента.

После расчета напряженно-деформированного состояния пластины происходит проверка выполнения критериев разрушения в каждом конечном элементе и заданная величина перемещений масштабируется таким образом, чтобы критерий разрушения выполнялся в единственном структурном элементе расчетной области, напряженно-деформированное состояние которого наиболее близко к моменту разрушения.

Жесткостные характеристики материала разрушившегося конечного элемента в зависимости от сработавшего в нем критерия разрушения изменяются согласно таблице. Далее, в итерационном режиме происходит пересчет полей напряжений и деформаций в расчетной области без изменения граничных условий с последующей проверкой выполнения критериев разрушения элементов и изменением жесткост-ных характеристик материалов элементов, для которых выполняется тот или иной критерий разрушения.

Описанная процедура повторяется до тех пор, пока при очередном пересчете полей напряжений и деформаций не окажется ни одного конечного элемента, для которого выполнялся бы тот или иной критерий разрушения. В этом случае последовательность действий повторяется с этапа масштабирования величины перемещений. В качестве условия окончания работы алгоритма выбирается достижение некоторого предельного уровня перемещений либо некоторого минимального значения суммарного усилия, действующего на нижней грани пластины. На основе вычислений строятся диаграммы деформирования расчетной области в координатах усилие-перемещение и картины зон разрушения.

Важной особенностью приведенного выше алгоритма является возможность моделирования стадийности процесса разрушения материала расчетной области: конечный элемент, претерпевший разрушение по одному из механизмов, сохраняет часть своей несущей способ- ности и может быть разрушен по другому механизму. Состояния конечного элемента в процессе многостадийного разрушения отражены на рис. 1. Цифрами обозначены механизмы разрушения, соответствующие приведенным в таблице.

Для пластины, представленной на рис. 2, проведено численное моделирование процессов структурного разрушения в условиях одноосного деформирования. Пластина представляет собой квадрат со стороной 10 см и круглым отверстием диаметром 2 см в центре. В качестве граничных условий для расчетной области задавалось жесткое перемещение и 0 на верхнем краю пластины и закрепление нижнего края пластины по оси x 1 . Остальные границы пластины считались свободными от нагрузок.

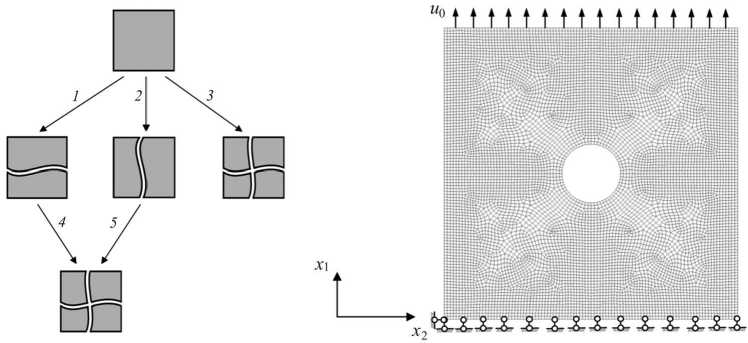
Рис. 1. Схема процесса разрушения по совокупности критериев

Рис. 2. Дискретизация на конечные элементы и граничные условия в расчетной области

Расчетная область разбивалась на четырехугольные конечные элементы таким образом, чтобы конечно-элементная сетка обладала горизонтальной и вертикальной симметрией с целью снижения влияния эффектов неоднородности дискретизации. Для проведения численных экспериментов по анализу возможностей представленной в данной работе математической модели был выбран упруго-хрупкий материал со следующими параметрами: E 1 = 142,8 ГПа, E ₂ = 9,13 ГПа, G 12 = 5,49 ГПа, v 12 = 0,3.

В первой серии экспериментов принималась гипотеза о том, что материал пластины разрушается только по одному из трех представленных в модели механизмов с одинаковыми прочностными константами для всех элементов.

На рис. 3-5 приведены полученные зависимости суммарного усилия реакции от перемещения верхней грани пластины, отражающие влияние выбранного критерия разрушения на механическое поведение области деформирования.

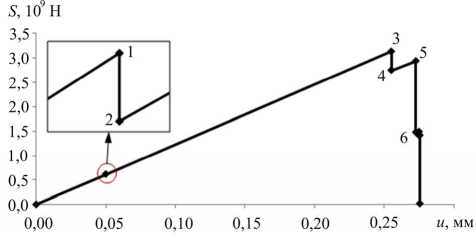
Ви ЯО

2  345

Рис. 3. Диаграмма деформирования и картины зон разрушения, построенные для процесса одноосного «жесткого» нагружения ортотропной пластины при действии механизма разрушения «1» (отрыв в направлении x 1 )

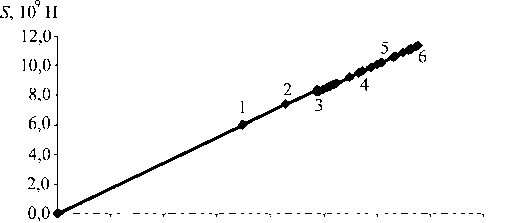
0,00 0,20 0,40 0,60 0,80 1,00 1,20   1,40 к, мм

1    2    3    45    6

Рис. 4. Диаграмма деформирования и картины зон разрушения, построенные для процесса одноосного «жесткого» нагружения ортотропной пластины при действии механизма разрушения «2» (отрыв в направлении x ₂)

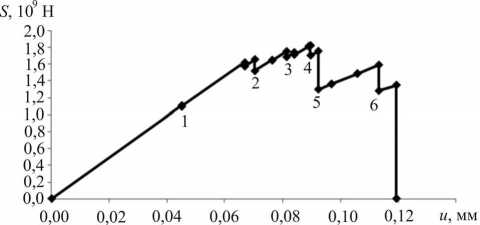
12345 6

Рис. 5. Диаграмма деформирования и картины зон разрушения, построенные для процесса одноосного «жесткого» нагружения ортотропной пластины при действии механизма разрушения «3» (сдвиг в плоскости x ₁ x ₂)

Видно, что выбор действующего критерия разрушения в значительной степени влияет на вид диаграммы деформирования и эволюцию зон разрушения в расчетной области. Так, картина зон разрушения пластины по механизму отрыва в направлении x ₁ представляет собой трещину, симметрично прорастающую из концентраторов напряжения по обеим сторонам перфорации к сторонам пластины. Диаграмма деформирования пластины, разрушающейся по механизму отрыва в направлении x ₂, остается линейной, так как структурные элементы, разрушенные по данному механизму, сохраняют способность сопротивляться нагрузкам в направлении x ₁.

Для дальнейшего исследования возможностей модели был проведен численный эксперимент, в котором предусмотрена возможность реализации всех рассмотренных механизмов разрушения. На рис. 6 показана диаграмма деформирования и картины эволюции зон разрушения для ортотропной пластины при одноосном «жестком» нагружении при разрушении по механизмам «1» и «3» (отрыв в направлении x ₁ и сдвиг в плоскости x ₁ x ₂) с соотношением предельных прочностных характеристик для данных механизмов разрушения £п cr / е₁₂ cr = 15/1.

Из картин разрушения материала в расчетной области по совокупности вышеприведенных механизмов видно, что в зависимости от того, как перераспределяются напряжения, на определенном шаге нагружения может преобладать тот или иной механизм разрушения.

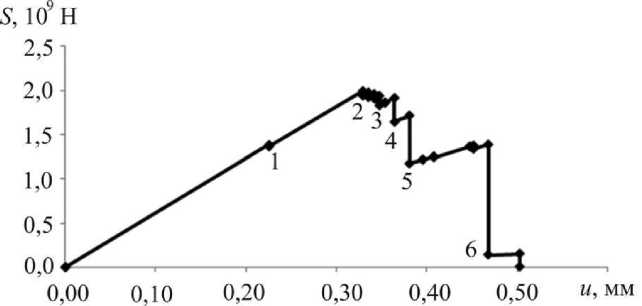
12 3456

- элемент, разрушенный от отрыва

- элемент, разрушенный от сдвига

Рис. 6. Диаграмма деформирования и картины зон разрушения, построенные для процесса одноосного «жесткого» нагружения ортотропной пластины при действии механизмов разрушения «3» и «1» (сдвиг в плоскости x ₁ x 2 и отрыв в направлении x ₁)

Важную роль при моделировании процессов разрушения играет учет стохастического разброса прочностных свойств структурных элементов расчетной области. Положим, что предельные прочностные характеристики элементов соответствуют трехпараметрическому закону распределения Вейбулла, функция распределения которого

F(е) = 1 - exp

е

^^^^^м

е

cr 0

cr

Vе a

—

е

cr 0

b

где е 0 r >  0 - параметр минимальной прочности, е^ - параметр характерной прочности, b > 0 - параметр формы. Параметры распределения связаны с коэффициентом вариации k v и математическим ожиданием (е) случайной величины следующими соотношениями:

/

е

cr 0

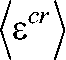
1 —

k v • C 1 C 2 ^— C 12

cr е a

k_v (е cr) V C 2 ^— C 12

cr

+ е0

где C ₁ = Г

V

1 +- , C 2 = Г . ь 7

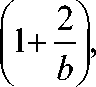
а Г( z ) - гамма-функция.

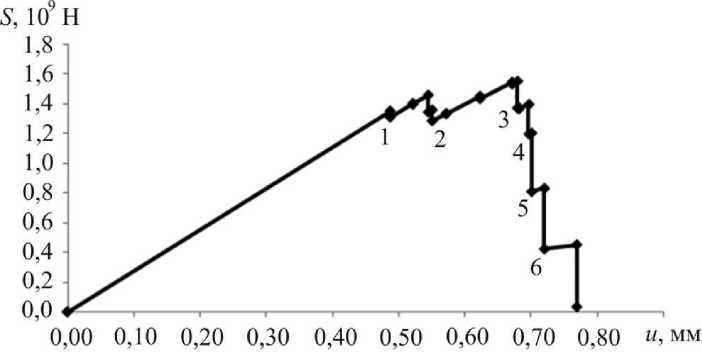
На рис. 7 представлена диаграмма деформирования и картины зон разрушения расчетной области под действием одноосного растяжения по совокупности механизмов разрушения «1» и «3» с коэффициентом вариации предельных прочностных характеристик структурных элементов k v = 0,3. Для данного случая параметр минимальной прочности е 0^r = 0,001, параметр формы b = 1,3.

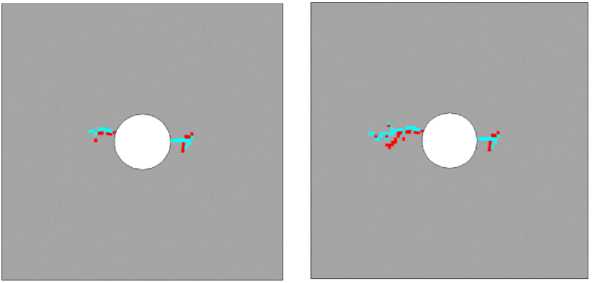
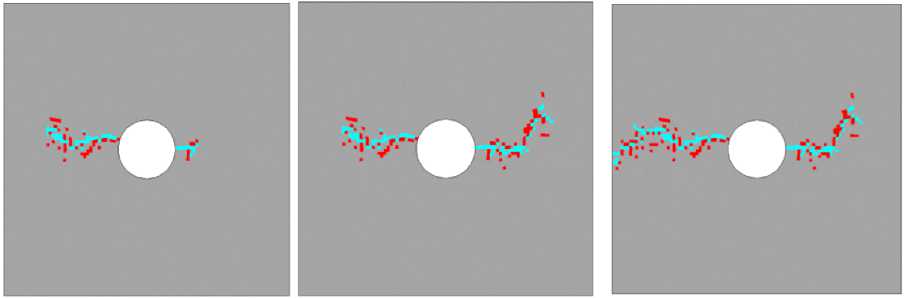
3                      4                         5

|     | - элемент, разрушенный от отрыва

I ■ - элемент, разрушенный от сдвига

Рис. 7. Диаграмма деформирования и картины зон разрушения, построенные для процесса одноосного «жесткого» нагружения ортотропной пластины при действии механизмов разрушения «3» и «1» (сдвиг в плоскости x 1 x 2 и отрыв в направлении x 1 ) с коэффициентом вариации прочностных свойств k v = 0,3

Из приведенных на рисунке картин эволюции повреждений видно, что стохастический характер прочностных свойств конечных элементов значительно влияет на протекание процесса разрушения ортотропной пластины, в частности, картина зон разрушения теряет свойство симметрии, процесс в меньшей степени зависит от расположения концентраторов напряжения.

Таким образом, приведенные данные демонстрируют возможность математического моделирования многоэтапного процесса повреждения деформируемого тела на основе использования совокупности критериев и схемы изменения свойств материала с учетом различных механизмов разрушения.