Исследование характеристик колебаний рабочих колес турбомашин с расстройкой параметров на основе моделирования уменьшенного порядка методом конечных элементов

Роторы турбомашин являются динамическими системами с конструктивной поворотной симметрией (циклически-симметричные системы (ЦСС)), которые позволяют исследовать их динамику на основе одного сектора. На практике в конструкциях всегда возникают отличия между лопатками (по массе, геометрии, материалу и т. д.) из-за изготовления, износа при эксплуатации и других факторов. Все эти малые отличия лопаток (так называемая расстройка параметров) нарушают циклическую симметрию. Причины расстройки параметров (неидентичность секторов) ЦСС могут быть разные. Чаще всего расстройка лопаток является маленькой величиной (т. е. собственная частота лопаток различна в нескольких процентах от номинального значения), но она может привести к возникновению резонансных напряжений, которые выше оптимальных на 20 % и более. Реальные увеличения максимальных напряжений на отдельных лопатках составляют от 0 до 20 % и зависят от размещения лопаток на диске. Можно предположить, что исследование расстройки будет играть большую роль при проектировании новых турбомашин, а также в правильной оценке и увеличении ресурса уже работающих [1; 2].

МУП используется, чтобы исследовать характеристики динамики ЦСС на основе одного сектора (рис. 1, б). В данной работе используется способ МУП, детально описанный в работах [3; 4], для исследования влияния расстройки лопаток на характеристики колебаний рабочих колес турбомашин, а именно: собственные частоты колебаний, формы собственных колебаний и максимум отклика вынужденных колебаний. Расчеты МУП проводятся МКЭ с помощью треугольных конечных элементов переменной толщины STI218, которые описаны в работах [5; 6]. Результаты данного исследования для рабочего колеса сравнены с экспериментальными данными и с результатами, которые получены с использованием МКЭ для ПМ (рис. 1, а) с использованием программного комплекса ANSYS. Погрешность результатов между методами МУП и ПМ и результатов метода МУП и результатов, полученных с помощью программы ANSYS, определены как

Общая схема моделирования уменьшенного порядка. Предположим, что степени свободы упорядочены так, чтобы получить блочно-диагональные формы при сборке матриц масс и жесткости всей конструкции. Они представлены в виде [ 4 ]

^£2 =

£ i =

расс      расс fМУП - fПМ .100 расс fПМ расс fANSYS .100, расс fANSYS расс f МУП

где f _М ^ра _У ^с _П ^с – собственная частота колебаний рабочих колес с расстройкой, полученная с использованием МУП; f _П ^р _М ^асс , f _A ^р _N ^ас _S ^с _YS – собственная частота колебаний рабочих колес с расстройкой, полученная с использования МКЭ для полной модели и программы ANSYS.

Реализация расстройки. Расстройка лопаток моделируется путем изменения эквивалентных жесткостей Л или изменения собственных частот лопаток, когда они стационарны (собственные частоты консольных лопаток). Эквивалентная расстроенная жесткость к -й формы n -й лопатки представлены в виде [ 7 ]

Л b,n = ( ю b , n ) = ( 1 + A f n )^Л ь , (2)

где Л ^ - жесткость к -й настроенной формы колебаний консольной лопатки и A f k - расстройка параметров k -й формы n- й лопатки.

В данной работе рассмотрим расстройку жесткости лопаток путем изменения модуля упругости лопаток. Тогда модуль упругости i -й лопатки определен как [ 3 ]

E i = ( 1 + A f ) E о , (3)

где E 0 – модуль упругости лопатки без расстройки, A f i - параметр расстройки i-й лопатки.

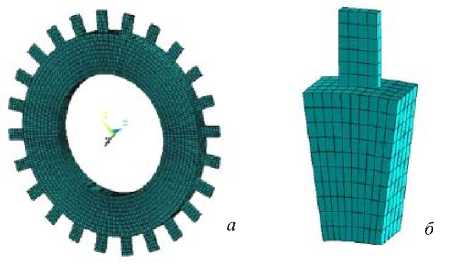
Рис. 1. Модель конечных элементов рабочих колес: а – полный диск; б – один типичный сектор

" Md 0 " I ® Mid 01 M = Mb _ = ^y , _ 0 _ 0 I ® Mb _ ■ Kd 0 " ■ I ® Kd 0 " K = Kb _ = ,       (4) _ 0 _ 0 I ® Kb _ где I – единичная матрица размера N; N – число секторов; M~d , K~d – матрицы масс и жесткости одного

~~ сектора диска; Mb , Kb – матрицы масс и жесткости

одной лопатки; символ ® обозначает оператор Кронекера, описанный в работе [4].

Перемещения одного сектора (рис. 1, б ) разделены на две части: перемещение диска с безмассовыми лопатками, которое имеет циклическое свойство (часть форм колебаний диска с лопаткой принадлежат степеням свободы лопатки и обозначаются δ ^d , а часть

диска - 9 ^d ), перемещение лопатки, закрепленной

жестко с диском δ ^b . Перемещения всей структуры

определены как [4]

9 d

0 δ ^b

b ,

где a – вектор обобщенных координат диска для всех T T TT форм, a = [a0 a1 ... aP] ; an - один вектор обобщенных координат, соответствующих n узловым диаметрам диска; P – максимальное число гармоник или максимальное число узловых диаметров; b – вектор обобщенных координат для всех N лопаток, Ь = [bT bT ... bN] ; Ь, - вектор обобщенных координат i-й лопатки.

Уравнение движения системы «диск–лопатки» в виде матрицы определено как [4]

TT

I d + 5 ^d M b 5 ^d 5 ^d M b 5 ^b

δ b^T

+

M_b δ ^d

Ib

• е

a

• е

b

a

+

+

^{+ (1 +} Y j )

.., m_b

δ b^T

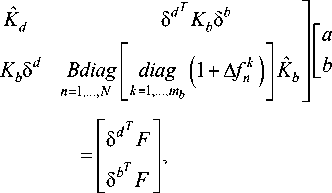
где I d =9 ^d M_d 9 ^d , K_d =9 ^d K_d 9 ^d - соответственно, матрицы масс и жесткости диска, когда все формы

с матрицей масс нормированы;  Ib = 5b Mb5b, bTb

K b = 5 K b 5 - соответственно, матрицы масс и жесткости N лопаток, когда все формы с матрицей масс нормированы; N - количество лопаток, £ k - коэффициент вязкого демпфирования; у - коэффициент демпфирования структуры; F - соответственно, вектор возбуждающих силы степеней свобод всех лопаток при сборке. Все матрицы в уравнении (6) детально описаны в работах [3; 4].

Характеристики колебаний рабочих колес турбомашин.

Собственные частоты колебаний . Метод МУП определяет собственные частоты колебаний рабочих колес без расстройки в зависимости от числа узловых диаметров и узловых окружностей. Число узловых диаметров одной формы колебаний нумеруется так, чтобы соответствовать одной фазе между смежными лопатками, определенной как [ 4 ]

Ф n = N- ( n = 0,..., P ),            (7)

где n - число узловых диаметров; N - количество лопаток рабочего колеса.

Формы собственных колебаний . В данной работе используем евклидову норму перемещений , чтобы исследовать формы колебаний рабочих колес с расстройкой и без расстройки. Для рабочих колес без расстройки евклидова норма определена в зависимости от числа узловых диаметров и узловых окружностей и является гармонической функцией при присутствии узловых диаметров (см. рис. 6, а , в ). Евклидова норма перемещений для собственных колебаний выражена скалярной величиной, называющейся формой относительных перемещений лопаток 5 r . Эта норма перемещений для i -й лопатки определена как [ 4 ]

N b

< Z 5 2, i

5 r = -Д==— ( i = 1,..., N),     (8)

N N b

< z z 52, n n=1 l j=1      _ где 5 j i - перемещение j-й степени свободы i-й лопатки; Nb - число степеней свободы одной лопатки; N -число лопаток в системе.

Максимум отклика вынужденных колебаний. В данной работе используем евклидову норму перемещений , чтобы исследовать максимальную амплитуду колебаний лопаток системы «диск-лопатки» с расстройкой и без расстройки. Для настроенной системы пик нормы перемещений всех лопаток одинаков, но это не так для расстроенной системы. Евклидова норма перемещений для вынужденных колебаний является скалярным выражением, оценивающим отклонение амплитуды лопаток, и определена как [ 4 ]

N b

5 n = Z 5 \п ( n = 1,..., N ),           (9)

V j = 1

где 5 _n - евклидова норма перемещений лопаток; N b -число степеней одной лопатки; 5 j _n - перемещение j- й степени n- й лопатки.

Определение возбуждающей силы. Возбуждающие силы - это гармонические функции от времени, отличающиеся фазой между секторами. Фаза i- й лопатки определена как [ 4 ]

Ф , = ^2П CN — ¹⁾ ( i = 1, ..., N ) (10) где C - порядок энергии возбуждений.

Вектор внешней возбуждающей силы представлен в виде [ 4 ]

F = { j /е ^Ф ... f^{j N} } T = NNe_{c + 1} 0 f , (11) где e _{C + 1} - ( C+ 1)-й столбец матрицы Фурье; f - вектор возбуждающей силы одной лопатки.

На физической модели (рис. 2) математическое уравнение распределения вектора газодинамических сил { f i } по длине лопатки может быть описано следующим видом [5]:

{ f } = [ 0 P y P x m z 0 0 ] T , (12) где P y = P y ( z , t ) и P x = P x ( z , t ) - возбуждающие силы по направлениям x и y ; m z = m z ( z , t ) - крутящий момент (рис. 2). Определение P_x , P y , m z детально описано в работе [5].

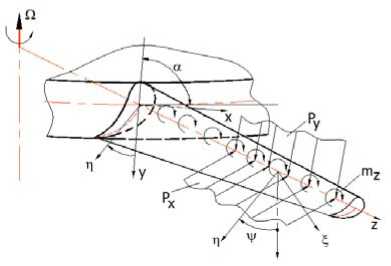
Рис. 2. Физическая модель лопатки ротора турбины под действием газодинамических сил

Результаты исследования. В качестве примера рассмотрим модельное рабочее колесо, содержащее 24 лопатки. Геометрические размеры и характеристики материала рассчитываемой конструкции: внутренний радиус 0,0135 м, внешний радиус 0,06 м, толщина диска и лопатки 0,002 м, длина лопатки 0,036 м, ширина лопатки 0,012 м, модуль упругости материала 210 ГПа, плотность 7850 кг/м³, коэффициент Пуассона 0,3. Возбуждающие силы приложены на все узлы пика каждой лопатки: { f i } = [ 0 1 1 1 0 0 ] T , коэффициент вязкого демпфирования £ k = 0, коэффициент демпфирования структуры у = 0,6 %. Параметры расстройки приведены в табл. 1.

Конечно-элементная модель сектора «диск– лопатки» для МУП и системы «диск–лопатки» при использовании МКЭ для ПМ на основе треугольных конечных элементов STI218, соответственно, содержит 174 и 3 312 степени свободы.

Результаты расчета собственных частот системы «диск–лопатки» без расстройки при использовании МУП, ПМ и программного комплекса ANSYS приведены в табл. 2 и на рис. 3.

Подобные результаты исследований колебаний рабочего колеса с расстройкой параметров по собственным частотам, погрешностям результатов и евклидовым нормам перемещений лопаток методов МУП, ПМ и программы ANSYS приведены на рис. 4–6.

Максимальная амплитуда перемещений лопаток, соответствующая порядкам энергии возмущения C = 5, приведена на рис. 7.

Таблица 1

Лопатка	1	2	3	4	5	6	7	8	9	10	11	12
Δ f i (%)	–0,52	–1,87	–1,82	–0,39	–5,01	–0,85	1,42	7,62	2,93	2,72	2,77	–4,92
Лопатка	13	14	15	16	17	18	19	20	21	22	23	24
Δ f i (%)	–8,07	–4,91	5,93	–6,92	–0,41	0,43	1,84	–5,47	2,39	3,81	4,11	3,92

Таблица 2

Формы	1	2	3	4	5	6	7	8	9	10	11	12
Эксп. [1]	210	265	340	501	681	803	922	938	961	1008	1027	1030
МУП	255,1	260,1	321	492	669	808	911,9	987	1041	1079	1104	1119
ПМ	255,1	260,1	321	492	669	808	911,9	987	1041	1079	1104	1119
ANSYS	265	284	318	491	655	778	865	929	973	1006	1026	1039
Формы	13	14	15	16	17	18	19	20	21	22	23	24
Эксп. [1]	1032	1386	1362	1723	2109	2714	3452	4102	4738	5112	5513	5983
МУП	1123	1461	1521	1737	2147	2713	3354	4002	4613	5155	5605	5947
ПМ	1123	1461	1521	1737	2147	2713	3354	4002	4613	5155	5605	5947
ANSYS	1043	1481	1524	1743	2208	2815	3447	4040	4567	5154	5655	5700

Параметры расстройки

Сопоставление расчетных и экспериментальных значений частот собственных колебаний модельного диска [8]

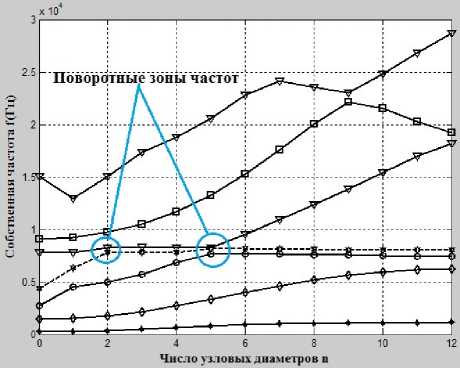
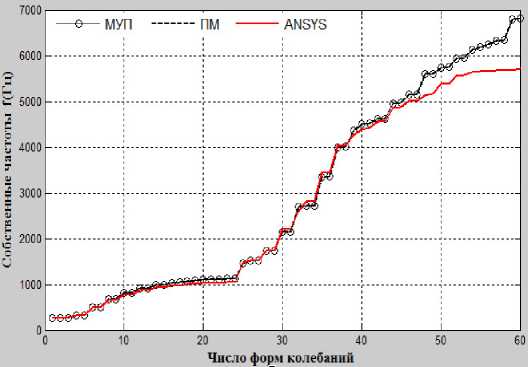
Рис. 3. График частот собственных колебаний «диск–лопатки» без расстройки в зависимости от числа узловых диаметров n и узловых окружностей m

Рис. 4. График собственных частот рабочего колеса с расстройкой параметров

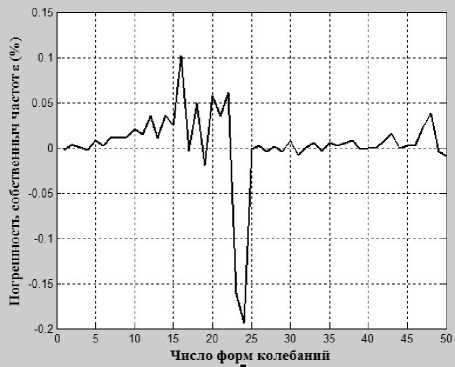
а

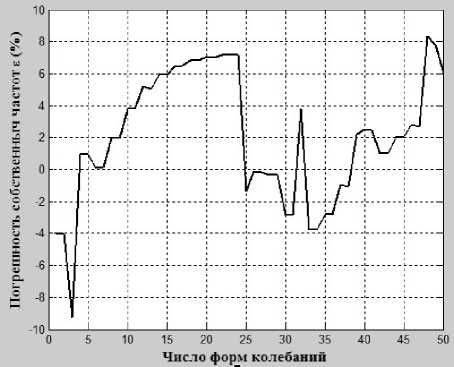
б

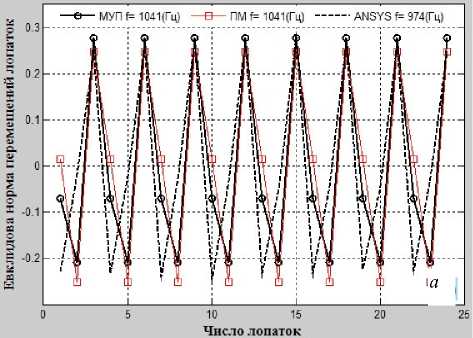
Рис. 5. Погрешность результатов собственных частот: а – при использовании МУП и ПМ; б – при использовании МУП и программы ANSYS

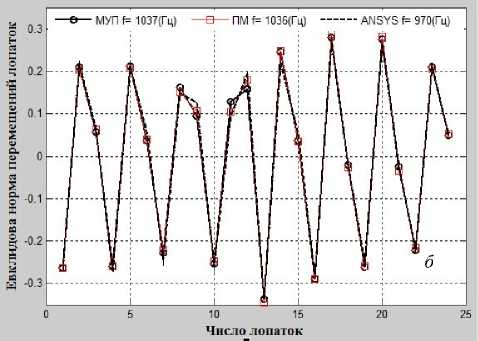
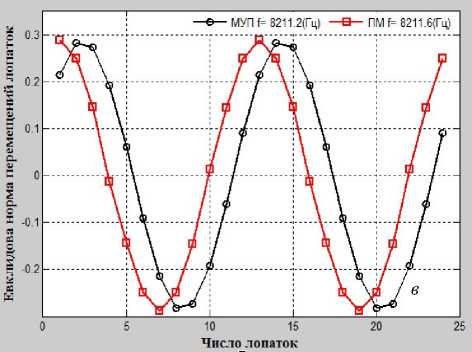
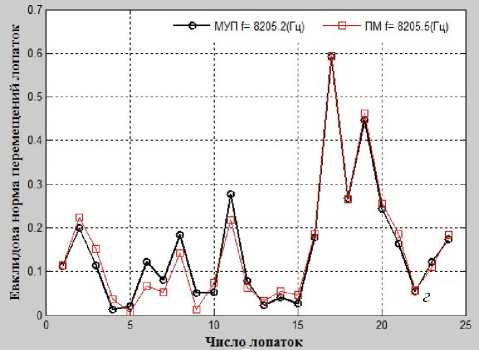
Рис. 6. График евклидовой нормы перемещений лопаток, соответствующей собственным расстроенным частотам

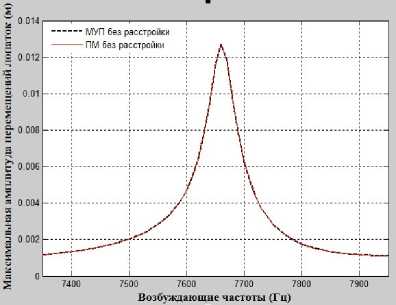
а

Рис. 7. График максимальных значений отклика вынужденных колебаний рабочих колес при С = 5

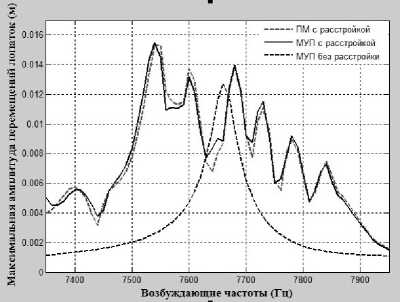
б

В работе представлен способ МУП для исследования колебания рабочих колес турбомашин без расстройки и с расстройкой жесткости лопаток. В этом способе использован подход составляющей формы: один сектор системы «диск–лопатки» разделен на две части. Это диск с безмассовыми лопатками, жестко защемленный на внутреннем радиусе, и консольная лопатка, жестко защемленная на поверхности между диском и лопаткой [ 9 ] . При этом используются матрицы масс и жесткости конечных элементов одиночной лопатки. Поэтому расстройка жесткости лопатки легко моделируется в расчете. Дополнительно при использовании МУП число степеней свободы расчета значительно уменьшается (из 3 312 степеней свободы при использовании ПМ число степеней свободы уменьшено до 174 для МУП), что снижает трудоемкость и численные затраты времени на ЭВМ.

Из рис. 3, 6 и 7 видно, что на графике собственных частот рабочих колес без расстройки в зависимости от числа узловых диаметров и окружностей часто появляются поворотные зоны частот. В этих зонах амплитуды собственных колебаний и максимальные амплитуды вынужденных колебаний рабочих колес даже с маленькой расстройкой жесткости сильно изменяются как качественно, так и количественно (рис. 6, г ; 7, б ).

Из табл. 2 и рис. 5 видно, что численные результаты МУП для рабочих колес без расстройки и с расстройкой МКЭ на основе треугольных конечных элементов STI218 хорошо совпадают с экспериментальными данными и результатами программного комплекса ANSYS. Полученные результаты 2-х этих методов очень близки. Однако использование треугольных конечных элементов STI218 позволяет учитывать модели со сложной геометрией сечения. Здесь представлено влияние расстройки жесткости лопаток на характеристику колебаний рабочих колес турбомашин. Эти результаты совпадают с выводами работ, которые опубликованы авторами Gisli Ottarsson [3], J. R. Bladh [4], и позволяют решать задачи чувственности колебаний и повышения прочности рабочих колес с расстройкой при проектиро- вании новых и эксплуатации старых конструкций турбомашин.

Данные исследования являются базовыми для дальнейшего анализа влияния расстройки параметров на долговечность рабочих колес турбомашин.