Исследование характеристик многоканального фазового ДОЭ, согласованного с модами Гаусса-Лагерра и оценка экспериментальных данных

В последнее время наблюдается устойчивый рост интереса к средствам передачи информации на расстояние. Сейчас наиболее перспективным направлением в этой области считается передача информации оптическими методами, например, по оптическим волокнам различной конфигурации. В настоящее время получили широкое распространение градиентные волокна с параболическим поперечным распределением показателя преломления. Моды Га-усса-Лагерра и Гаусса-Эрмита сохраняют поперечное сечение при распространении в этих волокнах [1]. Кроме того, они представляют собой полную ортонормированную систему, т.е. допускают разложение по ним заданного изображения с любой наперёд заданной точностью. Таким образом, решив задачу генерации линейной комбинации мод с заданными весами, можно формировать желаемые распределения световых пучков и использовать их для передачи информации по оптическому волокну.

Естественно, что для построения удовлетворительной системы связи помимо задачи разложения и трансляции изображения, необходимо решить задачу распознавания (селекции) мод, выбранных в качестве базиса разложения. Для генерации и селекции необходимых мод целесообразно использовать дифракционные оптические элементы (ДОЭ) [2]. Основное преимущество подобных устройств – непревзойдённое быстродействие, недостатки – всевозможные неточности, присущие аналоговым устройствам (ошибки дискретности, неизбежные технологические ограничения в процессе изготовления ДОЭ). В настоящей работе осуществляется построение ДОЭ, предназначенных для селекции и генерации мод Гаусса-Лагерра (ГЛ). Приводятся результаты численного моделирования их работы.

Часть данной работы посвящена решению проблемы анализа экспериментальных данных и оценке их погрешности. Единственный критерий, сравнительно легко доступный для наблюдения, по которому можно производить оценку погрешности получаемых изображений – картина распределения интенсивности в плоскости перпендикулярной оси пучка (как правило, в плоскости ДОЭ, либо же в фокальной плоскости). Чтобы сравнить полученные экспериментальные картины с теоретическими и оценить среднеквадратичную и геометрическую погрешности, нужно произвести ряд действий: совмещение центров изображений, масштабирование, поворот и нормировку. При отсутствии автоматизации процесса, это становится весьма трудоёмким делом. Для преодоления этих трудностей был разработан метод совмещения и оценки изображений.

Теоретические основы

Обобщенные моды ГЛ имеют вид:

^V nm ⁽ r . ф ) =

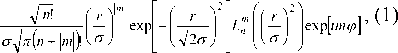
где a - параметр, характеризующий эффективную ширину модовой функции, r ²= x ²+ y ² – радиус в поперечной плоскости ( x, y – декартовы координаты в поперечной плоскости), ф=arctg(y/x ) - полярный угол в поперечной плоскости, L_n^m ( x ) – обобщённый многочлен Лагерра:

n

L m ( x ) = ( m + n ) £ ( - 1) k k = 0

k !( m + k )!( n - k )!

xk

( n,m ) – индексы моды, где n имеет физический смысл количества тёмных колец в поперечном сечении, а m – количества скачков фазы (см. рис. 1).

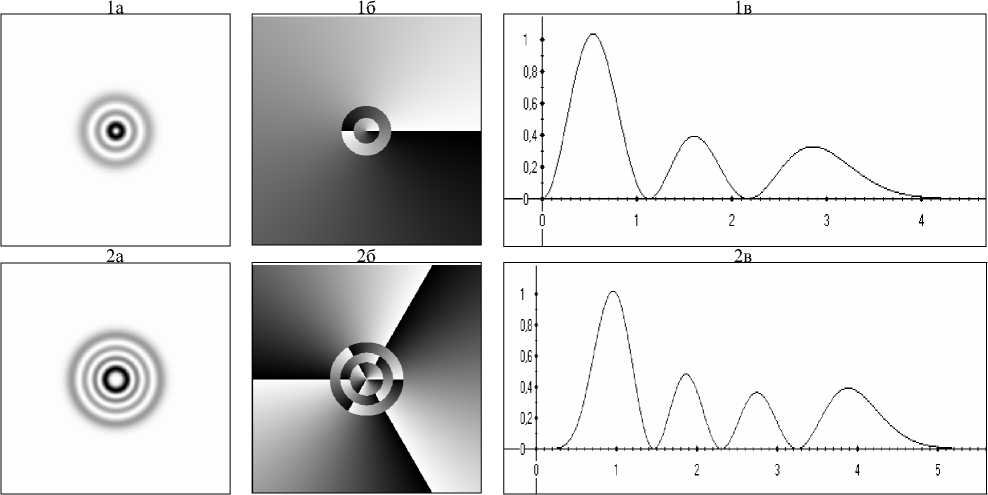
3а

3б

3в

Рис. 1. 1а, 2а, 3а – распределение интенсивности; 1б, 2б, 3б – распределение фазы, 1в, 2в, 3в – радиальное сечение интенсивности мод (n,m): (0,0) (2,-1) (3,-3), соответственно

Моды ГЛ распространяются в свободном пространстве по следующему закону:

U ( r , ф , z ) = exp

- ikz +

ikr ²    | r

-

4 R ( z ) ( x-^

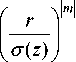
m Ln f r )

I ^ ( z ) J

V v u 7

^exP ^{[ -} iP nm ^{( z} ) ^{+ im}Ф^] ,

P nm ^{( z} ) = ⁽² n ⁺ | m | ⁺ 1) ■ ^a rCtg ( Z / Z о ) , ^{(4) z} 0 = ⁿ ^ 02 (x, ⁽⁵⁾ ^ ^{2( z} ) = ^ 0 ^{( 1 + z} 2/ ^z 0 ) , ⁽⁶⁾ R ( z ) = z ( 1 + z 2/ z ² ) , (7)

где z 0 – расстояние Релея, z – расстояние по оси модового пучка, измеряемое от его точки перетяжки ( z= 0), O 0 - эффективная ширина модовой функции в точке перетяжки (т.е. ст ₀ = ст ( z ) _z = ₀ ), X - длина волны лазерного излучения.

Моды ГЛ представляют собой полный набор ортогональных функций:

2 п м

f J ^nm (r, Ф)^kl (r, Ф)r d r d Ф = 5nk5mt , (8) 00

что позволяет представлять любую функцию в виде ряда по этим модам. Конечной суперпозицией мод ГЛ

NM

F ( r , Ф ) = SE C nm ^ nm ( r , Ф )’             (9)

n = 0 m | =0

варьируя N, M можно аппроксимировать изображение с любой наперёд заданной точностью. Коэффициенты C_nm в выражении (9) определяются по формуле:

2 п м

C nm = JJ F ⁽ r , Ф ^{) V} nm ⁽ r ,Ф ) r d r d Ф .           ⁽¹⁰⁾

Энергетический вклад каждой моды в пучок характеризуется квадратом модуля соответствующего коэффициента | C nm |².

Моды ГЛ являются собственными функциями Фурье-преобразования:

2 п м i JJ ^{2 n} 0 0

V nm ⁽ r , Ф ^)exp [ - irP C^os( ф ^- ^ ^{) ]} r d r d ф = ^(- 1 ) n i m V nm ⁽ P , ^ ),

что позволяет использовать их для эффективного ввода излучения в световые волокна.

ДОЭ для генерации пучков Гаусса-Лагерра

Для генерации заданной суперпозиции мод ГЛ целесообразно использовать ДОЭ. Теоретически, наиболее простым решением является амплитуднофазовый (АФ) оптический элемент, повторяющий амплитуду и фазу соответствующих мод. Однако АФ элементы весьма сложны в изготовлении и имеют низкую энергетическую эффективность, поэтому почти не используются на практике.

Наиболее эффективными являются чисто фазовые ДОЭ. Существует множество алгоритмов их расчёта. Наиболее простым из них является метод Лезема [3], предложенный для киноформов. В этом случае информация об амплитуде игнорируется (принимается постоянной), а учитывается только фаза. Однако такие фазовые элементы имеют очень большие погрешности формирования заданного светового поля, что делает это решение неудовлетворительным. Погрешность в данном случае возникает из-за того, что уравнивается энергетический вклад в изображение участков с большой и малой амплитудой. Таким образом, участки, на которые должно приходится от 1 до 10% энергии (они составляют 30–70% площади изображения), получают энергетический вклад, пропорциональный своей площади, что сильно искажает итоговую картину. Ясно, что для повышения качества фазовых ДОЭ необходимо «отсечь» эти участки. В [4] разработан метод знаковой функции с оптимизацией апертуры, который, в отличие от метода Лезема, позволяет часть информации об амплитуде сохранить и учесть ее в параметрах апертуры. В силу радиальной симметрии мод ГЛ, до 99% энергии сосредоточено в круге с радиусом равным радиусу наибольшего из колец мод. Поэтому имеет смысл «обрезать» ДОЭ апертурой этого радиуса. Оптимальный радиус апертуры точно находится путём минимизации среднеквадратичного отклонения Фурье-образа.

Кроме использования ДОЭ с апертурой нужного радиуса можно использовать другие способы «гашения» лишней энергии, например, освещение ДОЭ не плоской волной, а пучком с Гауссовским распределением амплитуды F ( r,ф ) = exp ( - r 2/2 ст ² ) . Тогда распределение интенсивности 1(г,ф)=ехр(-^/2 ^) , где σ – гауссовский радиус пучка. Оптимальный радиус σ находится путём минимизации среднеквадратичного отклонения Фурье-образа.

Пример для композиции мод (n,m): (1,1)+(2,2)+(2,11) (см. на рис. 2 и в таб. 1), е - часть энергии амплитудно-фазового эталонного распределения, проходящего через апертурную функцию (круг или гаусс), 8 - среднеквадратичное отклонение Фурье-образа).

Таблица 1. Параметры ДОЭ, согласованного с композицией мод(п,т): (1,1)+(2,2)+(2,11)

Тип ДОЭ	Радиус (пикселы)(изображение 350 x 350)	s (%)	5 (%)
Амплитудно-фазовый	–	100	0
Фазовый с круглой апертурной функцией	r=73	77,96	49,05
Фазовый с гауссовой апертурной функцией	σ=57	56,65	45,05

Рис. 2. Фазовый ДОЭ, освещаемый гауссовым пучком: а - распределение интенсивности; б - распределение фазы; 1в - распределение интенсивности Фурье-образа композиции мод (n,m): (1,1) (2,2) (2,11)

Многоканальные ДОЭ, согласованные с модами Гаусса-Лагерра

В задаче распознавания изображений инвариантно к их повороту в плоскости наблюдения целесообразно использовать пространственные фильтры, разделяющие амплитуду когерентного светового поля на отдельные дифракционные составляющие специальных ортогональных базисов, содержащих угловые гармоники [5]. Под угловыми гармониками понима- ются комплексные функции с единичным модулем и линейной зависимостью от полярного угла exp( 1тф). Такие гармоники появляются, например, при генерации многомодовых пучков Гаусса-Лагерра.

Сферическая линза фактически играет роль Фурье-анализатора, так как она раскладывает световое поле на плоские волны и пространственные Фурье-гармоники. Аналогично, комбинация «линза + ДОЭ» может быть названа анализатором Гаусса-Лагерра, если данный оптический элемент раскладывает ана- лизируемое световое поле по соответствующему базису [5-7]. Разложение по модам Гаусса-Лагерра может быть использовано при селекции поперечных мод на выходе многомодового волокна с параболическим профилем показателя преломления [8].

Функция комплексного пропускания (ФКП) ДОЭ такого анализатора представляется линейной комбинацией конечного числа базисных функций y_nm(x,y) взятых с заданными наклонами и единичными весами.

NM

Т(x, У) = Z Z ^nm (x, У)■ exP[i(«nmx + РптУ )] (12) n =0 m=0

Если такой ДОЭ поместить перед сферической линзой с фокусным расстоянием f и осветить световой волной с длиной волны X и амплитудой F ( x,y ), интенсивность света в точках (u_nm, v_nm) фокальной плоскости

Xf u nm       ^a nm ,

2п

= Xf R v nm   ~ P nm ,

2 п

будет приближённо пропорциональна квадратам модулей коэффициентов C_nm разложения комплексной амплитуды (10).

Пример многоканального ДОЭ, согласованного с модами ( n,m ): (1,1); (1,-1); (0,0); (2,2); (2,0); (2,-2); (4,0); (3,3); (3,-3) показан на рис. 3, а характеристики ДОЭ, включая дифракционную эффективность е и среднеквадратичное отклонение 5 , приведены в таб. 2 и 3.

Можно ввести ещё один критерий - геометрическое соответствие структуры изображений в Фурье-плоскости, например, совпадение центров изображений мод и радиусов колец на изображениях, 5 S . 5 S определяется формулой:

n

^ ( X Э i- X т?

5 s = i = 0 n ----------.                         (13)

Z X Э = 0

1а                                                1б Рис. 3. 1а – функция пропускания (интенсивность); 1б – функция	1в Номера мод ( n,m ):
пропускания (фаза); 1в – изображение в фокальной плоскости	(1,1)	(1,-1)	(0,0)
при освещении плоской волной фазового ДОЭ	(2,2)	(2,0)	(2,-2)
с круглой апертурной функцией	(4,0)	(3,3)	(3,-3)

Таблица 2. Параметры ДОЭ, согласованных с модами (n,m): (1,1); (1,-1); (0,0); (2,2) (2,0); (2,-2;) (4,0); (3,3;) (3,-3)

Тип ДОЭ	Радиус (пикс.) (изображение 350 x 350)	е (%)	5 (%)
Амплитудно-фазовый		17	0
Фазовый с круглой апертурной функцией	R =84	95,91	43,31
Фазовый с гауссовой апертурной функцией	с =50	57,06	34,36

Таблица 3. Погрешности генерации для ДОЭ, согласованных с модами (n,m): (1,1); (1,-1); (0,0); (2,2); (2,0); (2,-2;) (4,0); (3,3); (3,-3)

Фильтр	Фазовый с круглой апертурной функцией		Фазовый с гауссовой апертурной функцией
№ моды	5 (%)	5 s (%)	5 (%)	5 s (%)
(1,1)	48,66	9,24	37,09	9,25
(1,-1)	50,16	9,24	37,89	9,25
(0,0)	46,06	0	33,92	0
(2,2)	38,17	0	25,84	0
(2,0)	35,19	0	36,15	7,12
(2,-2)	38,80	0	27,70	0
(4,0)	45,07	13,50	36,61	27,99
(3,3)	33,65	26,92	27,72	25,34
(3,-3)	32,54	18,42	32,54	16,75

Из таб. 2 и 3 видно, что ДОЭ, рассчитанные на гауссовый освещающий пучок по сравнению с плоским освещающим пучком, обеспечивают меньшую среднеквадратичную ошибку формирования мод ГЛ при несколько большей геометрической погрешности.

Моделирование экспериментов по селекции мод Гаусса-Лагерра

На рис. 4 показано действие амплитудно-фазового, и фазового, оптимизированного по круглой апертурной функции фильтра, согласованного с модами ГЛ ( n,m ): (1,1) (1,-1) (0,0) (2,2) (2,0) (2,-2) (4,0) (3,3) (3,-3) при освещении их тестовой композицией мод с весами C 0,0 =C 2,0 =C 1,–2 =1. В таб. 4, 5, 6 даны численные результаты экспериментов.

2а

2б

Рис. 4. 1а, б – амплитуда; 2а, б – фаза в Фурье-плоскости после посылки композиции с весами C 0,0 =C 2,0 =C 1,–2 =1 для АФ фильтра и фазового фильтра с круглой апертурной функцией, соответственно

Таблица 4. Результаты вычислительного эксперимента для освещающей суперпозиции мод ГЛ с весами C 0 _, 0 =C_2, 0 =C_1,–2=1

Коэффициенты	На входе	Ожидаемые	АФ ДОЭ	|Δ с |	Фазовый ДОЭ	|Δ с |	Соотношение сигнал/шум
C 0,0	0,5000	0,5000	0,4978	0,0022	0,3905	0,1095	2,0000
C 2,0	0,5000	0,5000	0,5022	0,0022	0,5772	0,0772
C 1,-2	0,5000	0,0000	0,0000	0,0000	0,0000	0,0000
C 1,-1	0,0000	0,0000	0,0000	0,0000	0,0323	0,0323
Отклонение от ожидаемых, δ С				0,0440		0,1949

Таблица 5. Результаты вычислительного эксперимента для освещающей суперпозиции мод ГЛ с весами C 1,1 =3, C 2,0 =1, C 3,–3 =2, C 4,–7 =1, C 7,3 =2, C 8,–4 =4, C 9,1 =3

Коэффициенты	На входе	Ожидаемые	АФ ДОЭ	|Δс|	Фазовый ДОЭ	|Δс|	Соотношение сигнал/шум
C 1,1	0,5000	0,5000	0,6685	0,1685	0,5681	0,0681	0,6000
C 2,0	0,1666	0,1666	0,0753	0,0936	0,0323	0,1343
C 3,-3	0,3333	0,3333	0,2563	0,0770	0,3618	0,0285
C 4,-7	0,1666	0,0000	0,0000	0,0000	0,0000	0,0000
C 7,3	0,3333	0,0000	0,0000	0,0000	0,0000	0,0000
C 8,-4	0,6666	0,0000	0,0000	0,0000	0,0000	0,0000
C 9,1	0,5000	0,0000	0,0000	0,0000	0,0000	0,0000
Отклонение от ожидаемых, δ С				0,3329		0,4241

Таблица 6. Результаты вычислительного эксперимента для освещающей суперпозиции мод ГЛ с весами C_2, 0 =2, C_2,2=1, C 3 _,– 3 =1, C_5,4=2, C_7,1=4, C 8 _,– 3 =3

Коэффициенты	На входе	Ожидаемые	АФ ДОЭ	|Δ с |	Фазовый ДОЭ	|Δ с |	Соотношение сигнал/шум
C 2,0	0,5000	0,5000	0,6888	0,1888	0,6815	0,1815	0,4444
C 2,2	0,2500	0,2500	0,1623	0,0877	0,2542	0,0042
C 3,-3	0,2500	0,2500	0,1489	0,1011	0,0643	0,1857
C 5,4	0,5000	0,0000	0,0000	0,0000	0,0000	0,0000
C 7,1	1,0000	0,0000	0,0000	0,0000	0,0000	0,0000
C 8,-3	0,7500	0,0000	0,0000	0,0000	0,0000	0,0000
Отклонение от ожидаемых, δС				0,3779		0,4241

Погрешности для АФ ДОЭ возникают в результате того, что функции в формула (12) являются лишь приближенно ортогональными. ДОЭ дает хорошие результаты при соотношении сигнал/шум≥1, ухудшающиеся при соотношениях сигнал/шум=0,5 и ниже. Здесь «сигнал» равен энергетическому вкладу селектируемых мод (присутствующих в фильтре), а «шум» соответствует энергетическому вкладу паразитных (отсутствующих в фильтре) мод.

Полученные результаты позволяют говорить о пригодности фазовых фильтров для обнаружения той или иной моды в анализируемом изображении. Однако коэффициенты | C_nm |² находятся с недостаточной точностью. Чтобы повысить точность необходимо применять методы кодирования амплитудно-фазовой функции ДОЭ в фазовую [9].

Оценка экспериментальных результатов

Данный раздел посвящен решению проблемы анализа экспериментальных данных и оценки их погрешности. Единственный критерий, сравнительно легко доступный для наблюдения, по которому можно производить оценку погрешности получаемых изображений – картина распределения интенсивности в плоскости перпендикулярной оси пучка (как правило, в плоскости ДОЭ, либо же в фокальной плоскости). Чтобы сравнить полученные экспериментальные картины с теоретическими и оценить среднеквадратичную и геометрическую погрешности, нужно произвести ряд действий: совмещение центров изображений, масштабирование, поворот и нормировку. При отсутствии автоматизации процес- са, это становится весьма трудоёмким делом. Для преодоления этих трудностей был разработан метод совмещения и оценки изображений.

Основной проблемой является определение критериев совмещения, поворота и масштабирования изображений. Дело в том, что картины интенсивности для композиций обобщённых мод ГЛ зачастую бывают далеко не симметричны относительно оптической оси пучка. Эта ось легко определяется визуально, но найти её местоположение по картине интенсивности аналитическим путём представляется довольно сложной задачей. Таким образом, самая простая идея – совместить «центры масс» изображений, повернуть их и затем отмасштабиро-вать оказывается работоспособной только для простых случаев – отдельных мод и других, подобных, радиально-симметричных картин. В данном случае проблема заключается в поиске характерных точек изображения, по которым можно будет осуществлять совмещение и поворот, а в дальнейшем и масштабирование изображений. В разработанном методе выбираются две характерные точки изображения: «центр масс» и точка максимума.

Для отдельных мод и радиально-симметричных распределений

В случае радиально-симметричных изображений задача существенно упрощается. «Центр масс» совпадает с оптической осью пучка и, как правило, с точкой максимума.

Местоположение «центра масс» определяется следующим образом:

XC

=

E kj

Y C =

i , j

E l E ii^ j | y.

i j )

E x i j

где X C , Y C - координаты центра масс, I ij - интенсивность в точке (пикселе) изображения ( i , j ), x i, , y i, -координаты пиксела ( i , j ).

Для экспериментального и расчётного изображения определяется радиус, в который входит определённая доля (здесь выбрано 99%) энергии пучка. Тогда коэффициент масштабирования равен

Rэксп

Расчетное изображение поворачивается на угол ф , масштабируется с коэффициентом K_m и совмещается с точкой центра масс ( X C , Y C ). После этого запускается процедура точной доводки изображения, определяющая оптимальные значения параметров K_m и ( X C , Y C ) в небольшой окрестности найденных значений. Если этого окажется недостаточным, процедуру можно повторить ещё столько раз, сколько нужно для получения желаемой точности. Все действия производятся с расчётным изображением, поскольку осуществить их с ним программно проще, чем с экспериментальным, кроме того, не возникает дополнительной погрешности преобразований.

На рис. 5 показан пример использования метода для синтезированного тестового (рис. 5.1 (а) и экспериментального (рис. 5.2 (а) изображений.

Km --

R расч

1а

2а

2в

Рис. 5. 1а, 2а – анализируемые распределения интенсивности; 1б, 2б – расчетные распределения интенсивности; 1в, 2в – модуль разности анализируемого и расчетного изображений для синтезированной моды (1,1) и для экспериментально полученной с помощью 24-канального фазового ДОЭ моды (2,0), соответственно

Среднеквадратичное отклонение для синтезированного изображения бсинг=3,74%; это значение находится в пределах погрешности дискретизации изображения. Погрешность экспериментального изображения бэксп=37,03%. Эта величина связана с игнорированием амплитудной информации при расчете 24-х канального фазового ДОЭ, формировавшего моду, и согласуется с результатами, полученными в разделе 4.

Для не-радиально-симметричныхраспределений

Местоположение «центра масс» определяется по формуле (14).

Точка максимума ( X M , Y M ) - та точка изображения, в которой интенсивность достигает своего максимального значения. Для каждого из сравниваемых изображений (экспериментального и расчетного) определяется его вектор (см. рис. 6):

—

a расч

—*

a эксп

a расч ⁽ X M расч = ^аэксп ⁽ X M эксп

- X ,

C расч ^,

- X , C эксп ^,

У    - Ус

M расч C расч

Ф = arccos

^{( а} расч ' a эксп )

—

^ a расч| а эксп|

.

У - У.   )

M эксп C эксп

Рис. 6 . Определение вектора изображения (показан центральный фрагмент), 1 - точка максимума изображения, 2 – «центр масс» изображения

Коэффициент масштабирования K_m определяется отношением модулей векторов:

K

m

—— а. _ эксп

— a расч

.

Затем, определяется угол поворота изображения по углу между векторами:

Расчетное изображение поворачивается на угол φ , масштабируется с коэффициентом K_m и совмещается с точкой центра масс ( X C , Y C ).

После этого запускается процедура точной доводки изображения, находящая оптимальные значения параметров φ , K m и ( X C , Y C ) в небольшой окрестности найденных значений. Процедуру можно повторить несколько раз.

На рис. 7 показан пример использования метода для синтезированного тестового (рис. 7.1 (а) и экспериментального (рис. 7.2 (а) изображений.

Среднеквадратичное отклонение для синтезированного изображения δсинт=0,95%. Погрешность экспериментального изображения δэксп=24,19%. Основной вклад в эту величину вносят периферийные участки изображения

1а

2а

2б

Рис. 7. 1а, 2а – анализируемые распределения интенсивности; 1б, 2б – расчетные распределения интенсивности; 1в, 2в – модуль разности анализируемого и расчетного изображений для синтезированной композиции мод с весами C 1,1 =C 2,2 = C 11,2 =1 и для экспериментально полученной с помощью кодированного ДОЭ композиции мод свесами C_2,–2=–1, C_3,–1=–1.5, C_4,0=1, C_4,2=1, C_4,4=1,.5, соответственно

Оценка геометрической погрешности для экспериментального изображения

Из полученных выше результатов видно, что изображения, получаемые при помощи фазовых фильтров, хотя и имеют достаточно высокую среднеквадратичную погрешность (порядка 30%), визуально мало отличаются от теоретических. Следовательно, для нас представляет интерес не только традиционная среднеквадратичная погрешность, но также и «геометрическая» погрешность, т.е. среднеквадратичное отклонение координат характерных точек (локальных максимумов) экспериментального изображения от координат соответствующих точек теоретического изображения. Поскольку нахождение местоположения всех локальных максимумов экспериментального и теоретического изображений – достаточно сложная и ресурсоёмкая операция, в данной работе предложено оценивать геометрическую погрешность, проводя несколько сечений заданного изображения и оценивая среднеквадратичное отклонение координат локальных максимумов соответствующих сечений. Погрешность при этом определяется по формуле (13).

На рис. 8 и в таб. 7 показаны результаты вычисления геометрической погрешности для экспериментального изображения (рис. 8.1 (б). Разработанный полуавтоматический алгоритм нахождения максимумов изображения позволяет осуществлять обработку экспериментального изображения с помощью медианной фильтрации, а также находить максимумы на обработанном изображении в соответствии с заданными пользователем настроечными параметрами (полуширина окна сглаживания, минимальная крутизна пика, ширина верхней площадки пика).

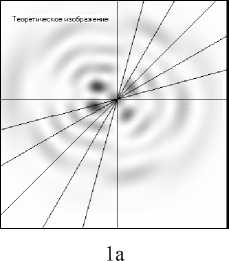
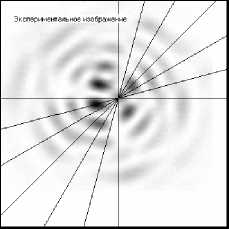
1б

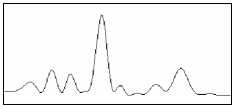
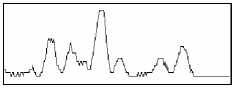
Рис. 8. 1а – расчетное изображение, 1б – экспериментальное изображение с линиями сечений; профили сечений изображений: а - расчетного изображения, б – экспериментального изображения, в – экспериментального изображения после применения медианной фильтрации при угле наклона сечения 0, 15, 30, 45, 60, 75 и 90 градусов.

(рисунки 2-8 (а,б,в), соответственно)

2а	2б д	2в д
3а	3б — а А	3в
4а	xJ v^ vV\/X>a 4б ^X/v^^xA^/x^^X1	4в
5а	5б	5в л Л
6а	6б	6в
7а	7б	vX^P^^ 7в

8а

8б

8в

Таблица 7. Геометрические погрешности экспериментального изображения (рис. 8.1 (б) при различных углах сечения

Угол сечения (гр)	0 о	15 о	30 о	45 о	60 о	75 о	90 о
δ S (%)	3,761	15,368	3,3823	17,702	1,261	4,293	5,035

Кроме того, алгоритм позволяет осуществлять сопоставление экспериментальных максимумов теоретическим как обычным наложением (совмещая элементы экспериментального и теоретического изображения), так и находя наиболее близкие максимумы теоретического и экспериментального изображений.

Большие значения погрешности при углах наклона сечений 15о и 45о связаны с несовпадением числа пиков экспериментального и теоретического изображений в результате искажений последнего, что легко видеть из рисунков 8,3, 8,5. Эти результаты можно скорректировать, усовершенствовав алгоритм распознавания и учёта пиков при вычислении геометрической погрешности изображений.

Заключение

В данной работе осуществляется синтез многоканального фазового ДОЭ для разложения световых полей по базису обобщённых мод Гаусса-Лагерра Ψ nm ( r,ϕ ), 0 ≤ n ,| m | ≤ N . ДОЭ можно использовать как для генерации сразу нескольких мод Гаус-са-Лагерра в различных дифракционных порядках, так и для селекции любой из 9-ти наперёд заданных мод в анализируемом пучке. Для генерации мод ГЛ несколько более точными оказываются фазовые ДОЭ, рассчитанные на освещение гауссовым пучком, чем плоским круглым. Полученные результаты позволяют говорить о пригодности фазовых фильтров для обнаружения той или иной моды в анализируемом изображении. Однако для точного определения весового состава мод необходимо применять методы кодирования. При этом отношение сигнал/шум не должно быть меньше единицы.

Для решения проблемы анализа экспериментальных данных и оценки их погрешности разработан метод, основанный на совмещения и подгонке расчетной картины по экспериментальным данным. При этом используется информация о величине и направлении вектора, соединяющего «центр масс» и точку с максимальным значением, на экспери- ментальной картине. Кроме среднеквадратичной погрешности, проведена оценка также и «геометрической» погрешности, т.е. отклонения координат характерных точек (локальных максимумов) экспериментального изображения от координат соответствующих точек теоретического изображения.