Исследование характеристик несжимаемого двумерного пограничного слоя методом Себиси

В настоящее время, на практике, достаточно часто приходиться сталкиваться с необходимостью решения нестационарных задач двумерного пограничного слоя. Обычно получить точное решение таких задач практически невозможно. Поэтому для решения подобного класса задач используются различные приближённые методы. В последнее время, в связи со значительным развитием компьютерной техники, предпочтение отдаётся конечно-разностным методам, алгоритмы которых наиболее пригодны для программирования и позволяют получить решение за относительно короткое время.

В данной работе рассматривается возможность применения метода Себиси для решения нестационарных задач несжимаемого двумерного пограничного слоя [1, 2].

Система уравнений для несжимаемого двумерного пограничного слоя, в общем случае, может быть записана следующим образом [2, 3]:

и = v = 0 при у = 0, и ^ U e при у ^^ .

где, u, v – продольная и поперечная компоненты скорости, х, у – декартовы координаты, U_e – скорость на внешней границе пограничного слоя, t – время, n – кинематический коэффициент вязкости.

При этом касательное напряжение _- u _′ v _′ может быть заменено в формуле (1) соотношением:

- u ′v′ = ε

m

∂ u д у ,

∂u ∂u ∂u

+u +v =

∂t ∂x ∂y

∂U

∂t

+U e ^{∂ Ue} + ∂ x

где e_m – коэффициент турбулентной кинематической вязкости. Данное соотношение используется для того, чтобы в дальнейшем можно было применять модель турбулентности Себиси-Смита.

Для использования метода Себиси, который в свою очередь основывается на неявном методе Келлера (схема “прямоугольник”), вводятся следующие переменные:

η=

д2 и д

+ν    - uv,

∂y∂y

∂u∂v

— + —= 0,

∂x∂y

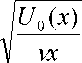
у ,

V = ^(vxU о)f (x, П, t),

где f(x,h,t) – безразмерная функция тока, а U₀(x) – некоторая функция, зависящая только от х. Тогда уравнение неразрывности в системе (1) тождественно удовлетворяется, если функция тока y определяется соотношением:

при этом граничные условия имеют вид:

∂ψ

U = ^, ∂y

∂ψ v =--.

∂x

Харитонова Анна Николаевна, начальник группы.

Используя правило дифференцирования сложной функции и соотношения (4) и (5) уравнение движения в системе (1) можно представить в следующей форме (штрихом обозначено дифференцирование по h ):

где

^(bf " ) ⁺ m+ 1 ff ^{- m} ( f ' ) ^{2 + m} i =

= x f f ^f - f f+^f )

( 5x     5x U0 51 J

,

u       x dU         £m f = , m=      -, b = 1 + —,

U ₀        U ₀ dx          v

x Г d U 5 U m =  U—- + —-

1 U0 ( e 5x 5t

•

При этом граничные условия (2) примут вид:

f = f = 0

f = U,/U 0

при n = 0, при n ^ n „ ■

Решение уравнения (6) с граничными условиями (7) осуществляется конечно-разностным методом Себиси в следующие четыре этапа:

• 1.    Уравнение (6) заменяется системой дифференциальных уравнений первого порядка (для этого вводятся новые переменные).

• 2.    Дифференциальные уравнения заменяются конечно-разностными с использованием формул центральных разностей.

• 3.    Полученная система нелинейных конечноразностных уравнений линеаризуется с помощью метода Ньютона и записывается в векторно-матричном виде.

• 4.    Система линейных уравнений решается методом матричной прогонки.

Более подробно метод Себиси рассмотрен в работах [1, 2]. На основе данного метода была разработана программа в среде программирования Delphi для решения нестационарных задач несжимаемого двумерного пограничного слоя. Программа позволяет получить решение уравнения (6) с граничными условиями (7) и, дополнительно, ряд характеристик пограничного слоя, в том числе местный коэффициент сопротивления трения ( c_f ) и толщину вытеснения ( d^* ).

В качестве тестовых задач, для проверки работоспособности метода Себиси и программы, были рассмотрены следующие стационарные задачи:

• 1.    Исследование пограничного слоя на плоской пластине, обтекаемой в продольном направлении.

• 2.    Обтекание круглого цилиндра в поперечном направлении.

Полученные решения данных задач хорошо согласуются с приближёнными решениями, приведёнными в работах Г. Шлихтинга и Л.Г. Лой-цянского [3, 4], что подтверждает правильность работы алгоритма и программы. Так, например, в случае обтекания круглого цилиндра отрыв наблюдается в точке равной примерно 105о, а в работе Шлихтинга [3] отрыв достигается в точке 104,5о.

Кроме того, для случая ламинарного нестационарного пограничного слоя, была рассмотрена задача обтекания движущегося круглого цилиндра радиуса R , причем скорость U_e на внешней границе пограничного слоя определялась формулой U_e ( x, t ) = 2 tU^ sin( x IR )■ А для случая как ламинарного, так и турбулентного тече-

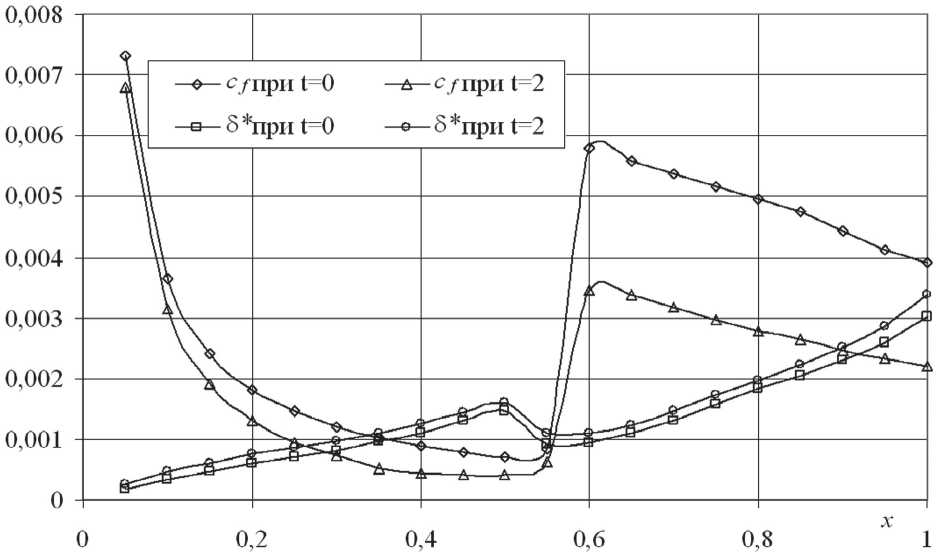
Рис. 1. Изменение местного коэффициента сопротивления трения и толщины вытеснения пограничного слоя в различные моменты времени для профиля крыла NACA 0012

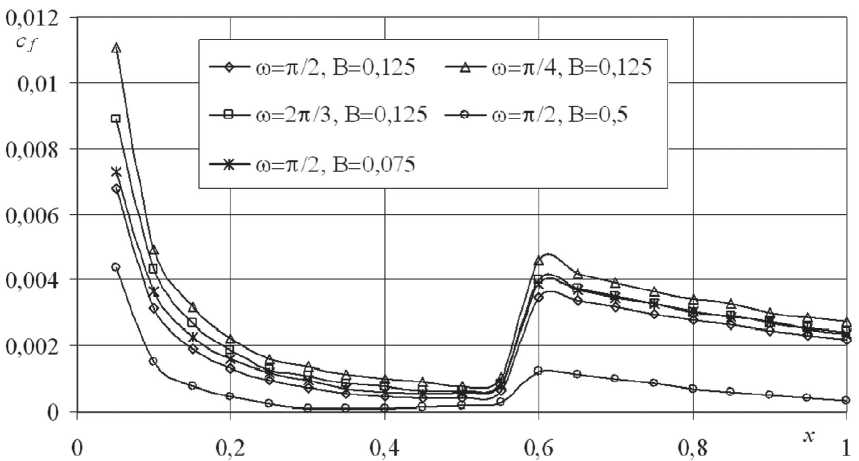
Рис. 2. Изменение местного коэффициента сопротивления трения для профиля крыла NACA 0012 при t=2

ния была рассмотрена задача продольного обтекания профиля крыла NACA 0012 для нулевого угла атаки, где U e ( x, t ) = U e ₀ ( x )(1 + В cos( ^ t )). В данной формуле, предложенной Себиси, В – амплитуда, а w – угловая частота (рад/с) . Примеры, полученных результатов для профиля крыла NACA 0012, представлены на рис. 1 и 2.

При этом графики, представленные на рис. 1 соответствуют результатам, полученным Себи-си и представленным в работе [1], что также подтверждает правильность работы алгоритма и программы. На рис. 2 приведены дополнительные расчеты изменения местного коэффициента сопротивления трения при различных значениях амплитуды и угловой частоты.

В заключение, следует отметить, что применение метода Себиси и разработанной на его основе программы, позволяет решать нестационарные задачи несжимаемого двумерного погранич- ного слоя за относительно короткое время и даёт возможность получить приближённые решения, которые в дальнейшем можно использовать для решения различных технических задач.

Данная работа проведена в рамках реализации ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009–2013 годы.