Исследование и анализ параметров многопереходных технологических процессов изготовления профилей сложного сечения для агрегатно-сборочного производства летательных аппаратов

процесса в автоматическом режиме, с возможностью получения взаимозаменяемых деталей с высокой степенью точности размеров, обладающих достаточной прочностью и жесткостью и высокими показателями ресурса изделий.

Исследование процессов деформации металла для деталей сложной конфигурации будем вести в предположении, что на отдельных участках заготовки происходит гибка и вытяжка. Рассмотрим случай вытяжки, когда наблюдаются большие усилия и деформации заготовки (рис. 1), где участок ab характеризуется растягивающими усилиями, участок bc – участок радиусного закругления, на котором возможно утонение заготовки, участок cd – участок с прямолинейными образующими.

Для оценки возможности применения теории вытяжки к технологическим процессам форм о-образования профилей необходимо разработать методику вычисления таких основных параметров вытяжк и как усилие пр оцесса, геометриче-

Рис. 1. Схема вытяжки при бол ьших усилиях и деф ормациях заготовки ские параметры оснастки, величины утонений и утолщений заготовки в зонах вытяжки.

Чтобы определить максимальную величину утонения, следует предположить, что наибольшее напряжение и соответственно наибольшее утонение наблюдаются в зоне границы перехода радиусной и цилиндрической частей. На радиусной части заготовки напряжения уменьшаются за счет активных сил трения в зонах контакта с инструментом и напряжений от изгиба. При расчётных малых степенях деформации за текущий переход считаем, что схема напряженного деформированного состояния заготовки линейная. Для расчёта интенсивности напряжений и деформаций используем уравнение кривой упрочнения степенного вида:

где G i , e i - интенсивности напряжений и деформаций, А, n – константы механических свойств, меридиональные напряжения приблизительно равны контактным g_p ~ n_s « 0 , то есть имеем схему линейного напряженно-деформированного состояния изотропного тела:

e_в ≠ 0, e_в + e_р + e_S = 0, e_р = e_S ,

A =------------, n = 8 „, 5 =       .

(1 - v_P ) • v;        ^{p p} i - ps

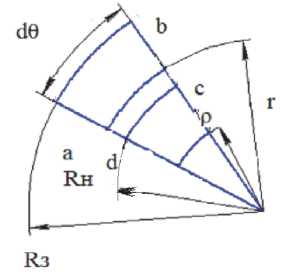
Рис. 2. Схема к определению деформаций в области радиусов переходов заготовки

окружностями, имеющими центр на оси симметрии и имеющие радиуса R₃ и r. Рассмотрим стадию вытяжки, когда этот элемент находится в положении, ограниченном радиусами R H и р .

Деформация любых тангенциальных точек определяется, если мы знаем длину до и после деформацию

e RH

= in kw, l_ab

eOp = ⁱⁿ

RH

R 3

Для линейной схемы напряженного состояния интенсивность напряжений равна G_p: : ст , = о- p и e i = e s ^ e s min . Тогда maxa _x = A • e n ,

es

' n_pMAX ) n

( A J

S min = S 3 • exP

' H_pMAX ) ⁿ

I A J

max ⁺ min ~ о

' cp =                 ~ S 3 .

Из условия постоянства объёмов заготовки и детали V₃ = V_Д, не учиты в ая вели ч ину упругой деформации F 3 • S ₃ = F д • S д , где S д - толщина детали по средней поверхности ( S_Д = S₃), получаем условие равенства площадей при вытяжке: F_Д = F₃, где условие равенства площадей детали и заготовки положено в основу определения деформаций при вытяжке любого элемента заготовки. Принимая с допустимой степенью точности схему деформаций аналогично как для фланцевой зоны заготовки, определим усилие процесса вытяжки и предельный коэффициент вытяжки по величинам деформаций как для фланцевой части (рис. 2).

Выделим на фланце бесконечно малый элемент двумя плоскостями, проходящими через ось детали, перпендикулярно к поверхности фланца и образующие между собой угол d в предположении, что если хотя бы один из размеров элемента abcd имеет бесконечно малый размер, то элемент является бесконечно малым, и что этот элемент образован двумя концентрическими

l d 'c ' l_dc

Длина lpdc - задается lpdч.< = р-d6.

Длина исходного состояния этого элемента l dc = r • d6 .

Находим величину тангенциальной деформации любого элемента с координатой р, если известна длина этого элемента до деформации или известны его координаты. Если известна зависимость r = f(p), то мы получаем величину деформации еq от независимой координаты р. Связь между r и r находим из условия равенства площадей рассматриваемых элементов до и после деформации.

F a' b ' c ' d" = F abcd ,

Fa'b'c'd" = ⁽ RH ^- P)) • ^d9,

F abcd = ( R 3 - Г 2 ) • d ^, F abcd = ( R 3² - r 2 ) • d6, r = ^R 32 ^- R H + p¹ .

Теперь можем найти еq.

Для того, чтобы определить две другие деформации еr и еq ,используем уравнение связи напряжений и деформаций:

e

s

^ee =

Cp + c>e ² •^9-cy_P

• ^e9 ,

ei

i

1         )

-1 ^d, ^e S

ei ⁺P^ne --------- • --------------------------------

Согласно используемой методики будем считать, что соотношение напряжений в процессе

формообразования есть величина постоянная:

Ор

—— = const и не зависит от упрочнения матери-

+ Oe " f2 " de -c p" f = 0,"

do p- f[ +op" df-ae" f2" de = 0.

ала и изменения его толщины.

Таким образом, рост напряжений за счет упрочнения в обоих случаях происходит пропорционально одному и тому же коэффициенту:

Найдем значения площадей:

f=_P" de " S , f 2 = S " dp.

■К упр

О О "  K упр

= const.

Если меняется толщина заготовки, то меняются и величины напряжений

СТр " KS          .

— ----= const.

С о " KS

Это условие позволяет определить деформации по отношению sr/sq и используя уравнения связей (найденных без упрочнения и изменения толщины) по известной одной из деформаций, найти другую деформацию.

+ 1

e s =

2 -

" ee.

Найдем напряжения, действующие на фланце без учета упрочнения и изменения толщины.

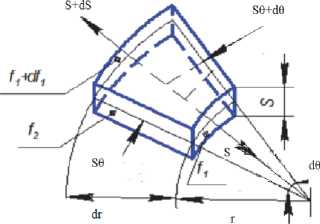
Рис. 3. Расчётная схема упруго-пластической деформации элемента заготовки

Подставив (2) и (3) в (1) получим: d p "—^ + CT +

Уравнение (4) содержит 2 неизвестных sr и sq.

Условие пластичности по максимальным касательным напряжениям:

О max ^—^min = P " ^S^.

P = 1 ^ 1,15 определяет схему напряженного состояния, в нашем случае /? « 1.

sr > 0, sq < 0, sК = 0, smax = sr, smin = –sq,

Условие пластичности (без учета упрочнения) (5) запишется следующим образом:

sr – (–sq) = s02,

Подставив в (4) уравнение (6), получим дифференциальное уравнение с разделяющимися переменными:

d do р = - 0-02--.

Р

Проинтегрировав уравнение (7) получим: sr= –s02 × ln r +C.

Граничные условия: sr = 0, r = RH, тогда посто-

янная интегрирования

C = s02 × ln RH.

В результате получим:

'р = ^02 "^ln

RH

.

При r = rД sr будет максимальным.

eo = In-, r

r = Rr32 - RH + p², e_p + e₆ + cs = 0. Эпюры

Составим уравнение равновесия на бесконечно малый элемент фланца заготовки.

Составим уравнение равновесия сил, действующих на координату Рqr = 0. По двум другим координатам уравнение равновесия сил составлять не будем в связи с тем, что они обращаются в тождества для заданных условий вытяжки:

2 p=2 p 2 Ps =2 Ps

(CTp^ da ^" (f1 + df1) +

изменения напряжений и деформаций на фланце при вытяжке

| lab\⁺ |lcd| = °"02

| la' b '| ⁺ |lc' d '| = °02

Op max (^"^min) ^<-'"02^.

Такая методика позволяет уменьшить радиус закругления в зоне деформации, соответственно снижаются дополнительные напряжения и

2 "^o" f2" sin d!"-Op" f.=0.

Раскрыв скобки, уберем величины, которые на порядок меньше остальных, а также учтем, d что sin—2— ~ —, тогда получим:

усилия для достижения заданных параметров деталей. Для повышения эффективности расчётов необходимо также учитывать величину возникающего изгибающего момента в местах неравномерного распределения напряжений

или когда напряжения имеют один и тот же знак:

MИ

op " f\ + d° P' d +°P" df++d^ / df

C02 " ^S

Необходимое дополнительное напряжение

определяем из условия равенства работ от внеш - них и внутренних сил.

А

ВН

Работа внешних сил

= АВ.

Авн = Act^ • 5 • b • (гм + 0,55) • dj, где b = 1 – единичная ширина,

5 • b = F, (r_M + 0,55) - плечо, Работа внутренних сил А_В = М_И.× dj.

Так как АВН = АВ, то pИ   5 • b • (rM + 0,55)

_______⁵ 2_______ _    02

4 • 5 • (гм + 0,55)   2 гм + 1

S

Таким образом, с уменьшением r ^ 0 ^ AcрИ^ 0-02 ■ по величине, то есть на первых операциях КВ наибольший, на последующих он значительно меньше, примерно в 1,5÷1,7 раза, но напряжения в первом и последующих переходах в опасном сечении должны быть одинаковы, они не должны превышать предел прочности, аналогично как и при вытяжке на последующих переходах опасными сечениями не должны являться участки, прежде недеформируемые.

Возможности последующих операций вытяжки объясняется снижением коэффициента вытяжки или уменьшением зоны сопротивления очага деформации, поэтому последнее равенство запишем следующим образом: на последующих операциях приняты одинаковые коэффициенты, их число n-1, а на первом переходе – отличные от вышеуказанных. Тогда:

^n-i

KB^_KB • KB2 .

Соответственно предельный ент вытяжки _КВПРЕД определим ^Gpmax^_Bfi , ИЛИ:

коэффици-

из условия:

p max '

L

• e^$TpP = в

A • (у>„ • In Kb ) " • ln|RH-| +

S

2 • rM + 1

S

+ Q • f 2-л-Rh•5

Другими словами, если процесс вытяжки про-

исходит в нестандартном режиме, то находим

КВПРЕД , то есть       < Kb , а число переходов при вытяжки определятся следующим образом:

KB

^R3, KB ^rÄ

R3 Ri R2    Rn-i или:

...             , rA Ri R 2    Rn-1

Прологарифмировав данное выражение, в результате получим: InK_B = ln|K_BJ + (n - i)ln|K_B2]. Это позволяет найти число переходов вытяжки:

n _ ln|KB - ln|KBi|+ _i.

ln K_B2

Разработанная методика расчётов параметров формообразования заготовок позволяет реализовать одновременную схему профилирования при автоматизации процессов деформации в многопереходных калибрах, также требуется меньшее число переходов вытяжки и соответственно меньшее число деформирующего инструмента.