Исследование и математическое моделирование литий-ионного аккумулятора

Перезаряжаемые литий-ионные аккумуляторы в настоящее время широко используются в качестве эффективных накопителей энергии во многих носимых электронных устройствах, включая портативные телефоны, портативные компьютеры, КПК и электробритвы [1, 2]. В частности, плотность энергии у них намного выше, чем у конкурирующих аккумуляторных систем, таких как NiMH и NiCd [3].

Для многих приложений, таких как автомобили или системы хранения энергии, литий-ионные аккумуляторы должны работать на пределе производительности, чтобы обеспечить рентабельные решения. Эксплуатация вне этих пределов приводит к быстрому износу и может привести к неконтролируемому поведению [4, 5].

Существует множество различных подходов к динамическому моделированию батарей [6, 7], которые описывают динамическое поведение элементов, аккумуляторных модулей или полных аккумуляторных систем.

Методики определения параметров модели

Моделью литий-ионного аккумулятора (ЛИА) является модель выходного Uвых(t) напряжения [8, 9], составляется по схеме замещения (рис. 1) и описывается следующим уравнением ивых (t ) = E (t) + R • i (t), (1)

где E ( t ) - ЭДС аккумулятора, В;

i ( t ) - ток заряда/разряда аккумулятора, A;

R ₀ - внутреннее сопротивление, Ом.

Более точной моделью ЛИА, описывающей процессы в аккумуляторе при изменении зарядно-разрядного тока, является модель Шеферда [10, 11]. Данное уравнение в режиме разряда аккумулятора выглядит следующим образом:

Vbat = Eo - K--Q--ibat - K Q^— + bat 0     Q + 0,1it        Q - it

+ A • e ( - Bt ) - R o • i bat ,                           (2)

где E o - максимальное напряжение аккумулятора, В;

R ₀ - внутреннее сопротивление, Ом;

K - поляризационная составляющая, В;

А - экспоненциальная составляющая, В;

В - инверсная экспоненциальная составляющая, А^ч^-1;

Q - полная емкость аккумулятора, А-ч;

it = J i * dt, i* - ток разряда аккумулятора, А.

Для определения значений параметров в выражении (2) необходимо воспользоваться экспериментальными данными ЛИА [12, 13]. Экспериментальными данными является зависимость напряжения батареи от емкости, представленной на рис. 2.

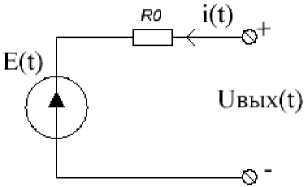
Рис. 1. Схема замещения аккумулятора

Fig. 1. Battery equivalent circuit

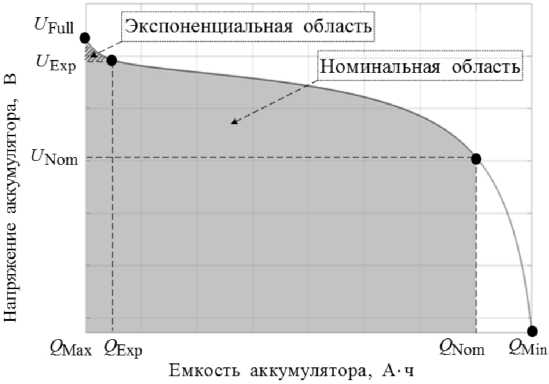
Рис. 2. Форма зависимости напряжения от емкости Fig. 2. Voltage-capacitance waveform

Значения параметров определяются по следующим формулам:

A = U fuII - U Exp ;                            (3)

B = —; Q Exp

K =

(U_M - U Nom + A ( e- BQ nom - 1)) • ( Q max - Q nom ) . Q nom

R

= U Nom

1 -n

0,2 Q Nom ’

E o = U Full + K - A + R o -ba_at ,                 (7)

где U Full – максимально допустимое напряжение аккумулятора, В;

U Exp – экспоненциальное напряжение аккумулятора, В;

U_Nom – номинальное напряжение аккумулятора, В;

Q_Nom – номинальная емкость аккумулятора, А·ч;

Q_Min – минимальная емкость аккумулятора, А·ч;

П - КПД аккумулятора, %.

Экспериментальная установка

Для снятия экспериментальных данных напряжения на литий-ионном элементе с течением времени была разработана специализированная измерительная установка, её принципиальная схема представлена на рис. 3.

Главным элементом установки является программируемая платформа на базе микропроцессора ATmega328p (U1). Она управляет процессом, измеряет напряжение на аккумуляторе и передает данные на компьютер (ПК) каждые 5 секунд через UART-интерфейс микропроцессора для последующего анализа. Процессор на основе измеренного значения напряжения считает ток разряда АКБ по закону Ома. Внешний вид установки представлен на рис. 4.

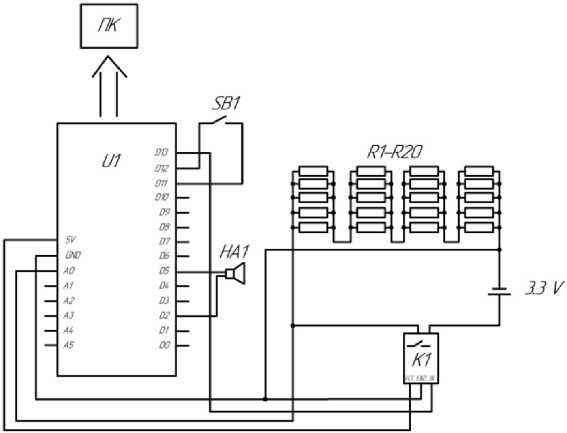
Рис. 3. Принципиальная схема установки Fig. 3. Schematic diagram of the measuring setup

Рис. 4. Установка для проведения эксперимента Fig. 4. Measuring setup for the experiment

Таблица 1

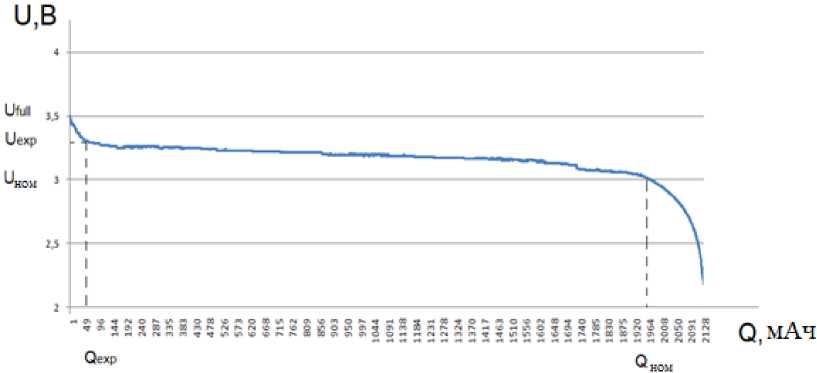
Рис. 5. Зависимость напряжения от емкости Fig. 5. Graph of voltage versus capacitance

Нагрузкой являются 20 резисторов (R1–R20), соединенных последовательно-параллельно для рассевания тепловой мощности, выделяющейся на них при протекании электрического тока. Поскольку резисторы углеродные, имеющие прецизионный класс точности и нагрев не прошивает температуру окружающей среды более чем на 10 градусов, то изменением их сопротивления можно пренебречь.

При нажатии на кнопку SB1 происходит запуск процесса разряда. По достижении критического значения напряжение реле К1 отключает нагрузку от аккумулятора, а динамик НА1 сообщает о прекращении процесса.

Полученные экспериментальные данные были сведены в табл. 1. Время эксперимента по разряду АКБ составило 9985 с. Рассчитанная в процессе

емкость составила 2128 мA·ч, что соответствует паспортным данным. Постоянный ток разряда составил 0,8 А.

После на основании экспериментальных данных, переданных через COM-порт компьютера, была построена зависимость напряжения батареи от емкости, на которой были выделены ключевые области для определения сходимости с формулой Шеферда (рис. 5).

Разработка моделив среде MATLAB /Simulink

Опираясь на модель литий-ионного аккумулятора Шеферда были рассчитаны основные параметры, требующиеся для подтверждения экспериментальных данных с теоретической базой (табл. 2).

Экспериментальные данные

Table 1

Experimental data

Время, с	Напряжение, В	Емкость, мA·ч
5	3,498	1
10	3,481	2
15	3,474	3
20	3,463	4
25	3,452	6
99…85	2…,2	21…28

Таблица 2

Параметры математической модели

Table 2

Parameters of the mathematical model

Параметр	Значение
А	0,3
В	15
K	0,036
R 0	0,39
E 0	3,43

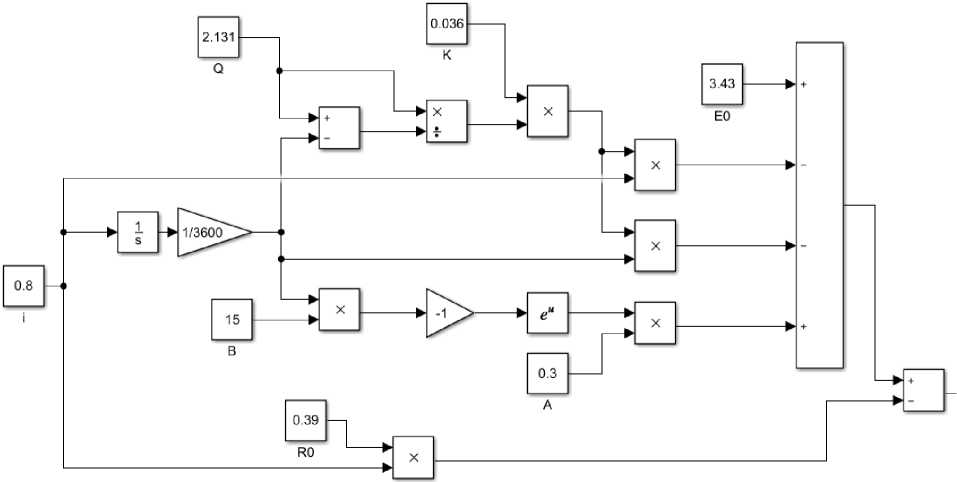
Рис. 6. Математическая модель литий-ионного аккумулятора в программной среде MATLAB/Simulink Fig. 6. Mathematical model of a lithium-ion battery in the MATLAB/Simulink

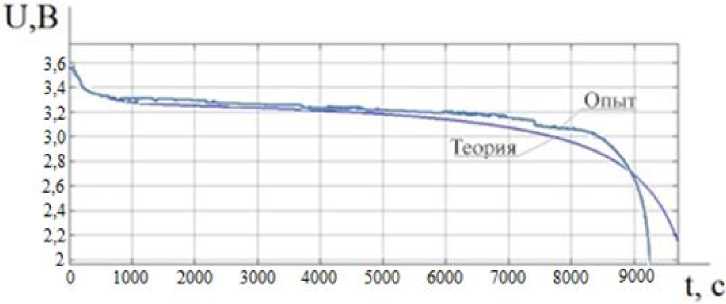
Рис. 7. Сравнение экспериментальных и расчетных данных Fig. 7. Comparison of experimental and calculated data

Далее была составлена математическая модель в программной среде MATLAB/Simulink (рис. 6).

На входе модели ток разряда, на выходе – зависимость напряжения от времени разряда.

После проведения сравнения результатов эксперимента и математической модели (рис. 7) было выявлено, что экспериментальная модель имеет хорошую сходимость с теоретической, и среднеквадратичное отклонение всех точек составило 2,6 %.

Заключение

На основе изучения областей применения литий-ионных аккумуляторов установлено, что они в настоящее время широко используются в качестве эффективных накопителей энергии во многих носимых электронных устройствах, КПК и в электромобилях. Поэтому исследования в области мо- делирования процессов заряда и разряда этих АКБ позволяют повысить качество предлагаемых моделей и использовать их в составе управляющих устройств.

Наиболее полной моделью разряда и заряда литиевой АКБ является модель Шеферда, которую можно дополнить и исследовать при помощи базовых законов физики, что и было проделано в этой работе. Как показали результаты эксперимента, использование микропроцессоров младшей серии (8 бит) с разрядностью АЦП 10 бит при применении алгоритмов фильтрации считывающих значений позволяет добиться приемлемых по точности результатов с погрешностью 2,6 %.

Также поскольку разработанная установка носит универсальный характер (она программируема), то она имеет возможность проводить замеры не только литиевых АКБ, но и свинцовых, никелевых и др.